线性代数之行列式的计算及其简化算法学习心得

第一次发文！

初入csdn，本人哈工大大一船舶与海洋工程专业，因为想学计算机相关专业再加上爹是搞开发的程序猿，为大二辅修计算机做好准备，准备开始着手进行系统的计算机学习啦～

---

前言

最近在准备线性代数的期末考试，发现一个很有启发性的小问题和大家分享。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、计算矩阵——行列式

行列式的定义

行列式的定义在这里：

先来一个三阶行列式的定义。我们的教材是英文版哦～对我来讲，更有助于深入地理解概念以及本质。

可以看出行列式的定义比较简单（analogous to 2 by 2 matrix），对矩阵的第一行进行展开到2 * 2的矩阵，即可得到3 * 3矩阵的行列式。

对于一般的矩阵来说，定义如下：

也是很简单的，类比三阶行列式即可得到高阶行列式的定义——按照第一行展开就可以了。

二、行列式的算法

1.按照定义进行计算

由高阶行列式一级一级展开到低阶行列式……一直展开到二阶行列式，然后用公式算出得到这个高阶行列式的value。

但是这么运算会导致计算量极其庞大，具体表现在下面的图片：

上面的NOTE表明了计算一个行列式如果运用定义展开进行直接计算的话，虽然算法结构简单明了，但是给计算机可造成了不小的麻烦。

例如，以后在学习特征值、特征向量(Eigenvalue Eigenvector)时，计算特征多项式(Characteristic polynomial)时，对行列式的计算是必须的，但是计算机的算力假如仅仅运用定义逐级展开，在处理一个较大的矩阵时是极其有限的，note中的例子表明这种算法效率极其低下。如何去解决这个问题呢？

2.简单行列式计算——三角矩阵行列式

三角矩阵的例子如下

这是一个看起来长得很“整齐”的矩阵。可以发现，矩阵的主对角线(Main diagonal)下方的位置全都是0，上方的数字是随机的。

而如何计算这个“三角矩阵”的行列式呢？

先引入一个定理——Laplace Expansion Theorem

这个定理就是告诉我们，可以不用像定义一样只用第一行来进行行列式展开，完全可以用任意的一行或者一列进行展开，使我们更进一步运用定义来处理矩阵的行列式，把问题变得更加简单。

提示：不要忘记每一个子式的符号哦

接下来，运用这个Laplace Expansion Theorem我们可以更加简单地计算三角矩阵的行列式了！

对第一列进行展开（第一列只有第一项不是0，其他全都可以消掉）：

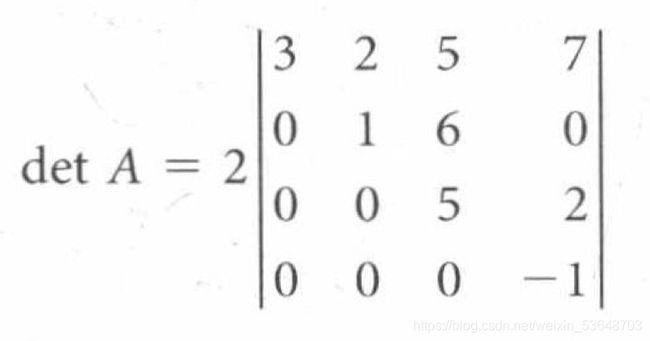
照葫芦画瓢，依次可以得到最终的三角矩阵A行列式：

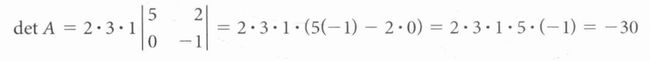
可以得到一个惊人的结论：三角矩阵的行列式是主对角线的乘积！
（看定理：）

这个定理是非常有用的，对于简化行列式计算起到了至关重要的作用。

3.矩阵行列式的基本行变换

众所周知，矩阵可以进行那个比较经典的高斯消元(Gauss Elimination) 或者高斯-乔丹消元(Gauss-Jordan Elimination)来解线性方程组。那行列式可以这么玩嘛？如果能化简成一个类似于行阶梯形(Row echelon form)的东东，是不是就可以化成类似三角矩阵进行计算了，这样子一般行列式的计算，化简完毕后就可以依照三角矩阵行列式的计算来进行计算了！问题来了，可以吗？

经过一番推导，给出了几个行列式的性质，表明这样是可行的！

运用这些性质，完全可以对行列式进行行变换（当然规则有点不同，看不懂英文的童鞋可以自行问度娘）。具体如何变换不再赘述。

进行完行变换后，如果矩阵可逆，一定会得到一个规规矩矩的三角矩阵（参见可逆矩阵基本定理）。如果不可逆，行列式肯定为0（有一行是0，展开后一定全是0）。接下来，就可以舒舒服服地用三角矩阵计算行列式的 方法来计算行列式了！

---

三、计算量的差别

对于一个n阶行列式来说，如果，运用计算机计算行列式应用定义或者是Laplace Expansion Theorem，计算量将会是这个数：

这个数比n的阶乘(n!)要大。

如果运用行变换，再运用三角矩阵计算行列式的方法来计算行列式，可以得到这个计算量：
只有：n的三次方！

相比于定义展开来进行计算，此方法会简单很多，省去很多不必要的计算，使计算机工作的负担减轻许多。

当然，计算矩阵行列式的方法还有很多种，但是优先选择哪一种方法能带来计算量的减少是我们一定要注意的事情。

在处理二维数组时，尤其是对图进行变换以及数据存储等等问题时，一定有着很广泛的应用。

码字不易，感谢观看！
以后会持续更新学习心得！
不局限但主要为：数学类、计算机类、工程类。