关于灰度共生矩阵的一点知识（MATLAB）

目录

一、基本理论

1、背景

2、概念

3、含义

4、例证

5、规律

二、特征量

1、对比度(contrast)

2、角二阶矩(Angular Second Moment, ASM）

3、熵(entropy）

4、逆差矩(Inverse Different Moment, IDM）

5、相关性(correlation)

三、MATLAB自带函数

1、函数名

2、功能

3、基本用法及描述

四、MATLAB代码实现

1、获取GLCM

2、使用MATLAB代码实现灰度共生矩阵的计算

2、依据GLCM计算角二阶矩、熵、对比度、相关性

五、总结

参考链接

---

一、基本理论

1、背景

  20世纪70年代，R.Haralick等人提出了用灰度共生矩阵（Gray-level Co-occurrence Matrix，GLCM）来描述纹理特征。

2、概念

  灰度共生矩阵(GLDM)的统计方法是20世纪70年代初由R.Haralick等人提出的，它是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下，提出的具有广泛性的纹理分析方法。[^1]

  灰度共生矩阵是像素距离和角度的矩阵函数，它通过计算图像中一定距离和一定方向的两点灰度之间的相关性，来反映图像在方向、间隔、变化幅度以及快慢上的综合信息。

3、含义

  灰度共生矩阵实质上是一幅图像中两个像素灰度级的联合直方图，是一种二阶统计量。

  普通的灰度直方图是对图像上单个像素具有某个灰度进行统计的结果，而灰度共生矩阵是对图像上保持某距离的两像素分别具有某灰度的状况进行统计得到的。

  取图像(N×N)中任意一点 （x，y）及偏离它的另一点 （x+a，y+b），设该点对的灰度值为 （g1，g2）。令点（x，y） 在整个图像上移动，则会得到各种 （g1，g2）值，设该灰度图像的灰度值级数为 k，则（g1，g2） 的组合共有 k² 种。对于整个图像矩阵，统计出每一种 （g1，g2）值出现的次数，然后排列成一个方阵，再用（g1，g2） 出现的总次数将它们归一化为出现的概率P（g1，g2） ，这样的方阵称为灰度共生矩阵。[^2]

4、例证

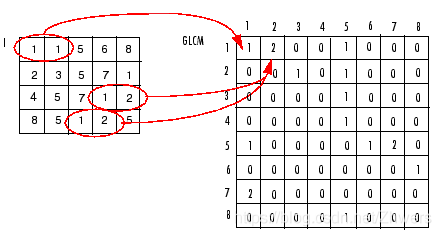
  下面以图示解释如何灰度共生矩阵的生成方法，下例中以GLCM表中的（1，1）点为例，GLCM（1，1）即为在左边的整个图像灰度矩阵I中寻找“两灰度值均为1且两像素点水平相邻的像素点对”的数量，例中GLCM(1,1)=1，即只有一对水平相邻的像素点对满足两灰度值均为1。同理可得GLCM(1,2)=2。

  GLCM表其实是所有像素点可能的排列方式以及每一种排列方式存在于该幅图像中的数量。也就是，在图像矩阵I中，像素灰度值为i和像素灰度值为j的两个像素点组成的点对(i,j)的数量，就是GLCM(i,j)的值。如果对GLCM表进行归一化之后，表中的每个值代表的就是每一种排列方式存在于该幅图像中的概率。

  在这里，有一个特殊的知识点，我们可以认为其实图像中任意两个像素点都是在某种条件下的相邻点。即，点f(x,y)与点f(x+a,y+b)相邻，构成这个相邻的条件就是，两个像素点在x方向上相隔a个单位，且在y方向上相隔b个单位。像是上例中所说的G(1,1)=1，就是表示在灰度矩阵I中，存在两个灰度值为1的点在a=1且b=0的条件下满足相邻而构成的点对只有一对。

  概括来说，点A与点B存在以下四种条件下的“相邻”：

         ①当a=1且b=0时，点B在点A的右边，AB连线与x轴正方向构成0°夹角，称为“水平相邻”；

         ②当a=1且b=1时，点B在点A的右上角，AB连线与x方向构成45°夹角，称为“对角相邻”；

         ③当a=0，b=1时，AB连线与x轴正方向构成90°夹角；

         ④当a=-1，b=1时，AB连线与x轴正方向构成135°夹角。

  为什么要讲这个特殊的相邻呢？因为我们在计算一幅灰度图像的灰度共生矩阵的时候，我们可能需要依据实际情况更改计算的粒度，对于纹理变化缓慢的图像我们可能不必要计算到a=1或者b=1这么细致的程度，这时候我们就可以适当扩大a或b的数量，依照上述概念，被计算到的两个像素点还可以看作是“相邻”的，不过它们之间的间隔变大了而已。

5、规律

  对于一幅图像的灰度共生矩阵，原图像的纹理变换越缓慢，则灰度共生矩阵的对角线上的数值就会比较大；而纹理变换越快，则对角线上的数值就会越小，而对角线两侧的数值会增大。

二、特征量

  尽管一幅图像的灰度共生矩阵能够反映出图像灰度关于方向、相邻间隔、变化幅度等方面的综合信息，但由于灰度共生矩阵的数据量通常比较大，所以一般不会直接对矩阵进行操作，而是提取出它的一些特征量来描绘原图像的特征信息，如能量、熵、对比度、均匀性、相关性、方差、差平均、差方差等。因为项目需要没有研究太多特征量，下面选择部分名词进行解释[^3]

1、对比度(contrast)

  对比度是一个常见的度量名词，可以用于反映图像的清晰度和纹理的沟纹深浅，它实际上度量的是图像灰度矩阵的值是如何分布以及图像中局部变化的程度的。纹理的沟纹越深，反差越大，图像局部越清晰。

P（ｉ，ｊ）是指归一化后的灰度共生矩阵

2、角二阶矩(Angular Second Moment, ASM）

  又称为能量，能量变化反映了图像灰度分布均匀程度和纹理的粗细度。若灰度共生矩阵的元素值相近，则能量较小，表示图像纹理较为细致；若如果其中一些值大而其他值笑，则能量值会比较大。能量值大表示一种较为均匀、变化比较规则的纹理模式。

3、熵(entropy）

  图像会包含信息量的随机性度量。当共生矩阵中所有值均相等或者原图像矩阵的像素值表现出最大随机性时，熵最大。因此，熵值表明了图像灰度分布的复杂程度，熵值越大则图像越复杂。

4、逆差矩(Inverse Different Moment, IDM）

  逆方差反映了图像纹理局部变化的大小，若图像纹理的不同区域之减较为均匀，变化缓慢，那么逆方差的值会比较小。

5、相关性(correlation)

   相关性反映了图像纹理的一致性.如果图像中有水平方向的纹理,则0°灰度共生矩阵的COR会大于其他几个角度方向的灰度共生矩阵的COR值

三、MATLAB自带函数

  MATLAB作为一个臃肿庞大但极为强大的数据处理软件，这种计算灰度共生矩阵的函数自然也是有的，

1、函数名

  graycomatrix()

2、功能

  创建灰度共生矩阵

3、基本用法及描述

  使用方法：

         ①glcm=graycomatrix(I)

         ②glcms=graycomatrix(I,param1,val1,param2,val2,...)

         ③[glcms,SI]=graycomatrix(...)

  描述[^4] ：

     函数graycomatrix(I)产生图像I的灰度共生矩阵GLCM，它是通过计算两灰度值i，j在图像I中水平相邻的次数得到的。上面的用法①就是最基本的用法，使用默认参数输出图像I的灰度共生矩阵glcm。在计算过程中，graycomatrix()函数会先将图像I归一化到指定的灰度级，再计算GLCM，这是因为动态地求取GLCM区间代价过高；而这个指定的灰度级默认情况下是8灰度级，如果你的I是一个二值图像，这个指定的灰度级就是2级。

     用法③[glcm,SI]=graycomatrix(...)除了返回一个灰度共生矩阵glcm外,还会返回一个归一化的灰度图像SI,也就是实际上被用于计算灰度共生矩阵的那个灰度图像,因而SI中的像素灰度值取值范围在默认条件下就是[1,NumLevels].]

     上面的用法②是①的加强版，可以修改一些默认的参数。

     常用的可以修改的参数如

     'NumLevels'，可以指定归一化后的灰度级数目，如将NumLevels设定为16，就是将整个图像的灰度值映射到[1,16]这个区间中。NumLevels决定了灰度共生矩阵的大小，默认值是8。

     'GrayLimits'，是两个元素的向量[low,high]，指明图像中的灰度值线性归一化后的的灰度级别范围：不大于low的灰度值将被置为1，不小于high的灰度值将被置为'NumLevels'。这一参数如果不被指定，默认情况下，low=min(I(:))，high=max(I(:))。

     'Offset'，是一个p*2的整数矩阵，可以用于指定目标像素点对的'相邻'条件[^5] ，矩阵中的每一行是一个含有两个元素的向量，[row_offset,col_offset]，通过修改这两个参数的正负性、大小就可以指定目标像素点对在特定角度、特定距离上的“相邻”。

四、MATLAB代码实现

1、获取GLCM

glcm=graycomatrix(I);    %仅获取GLCM
[glcm,SI]=graycomatrix(I);    %既获取GLCM,又接收归一化的灰度图像SI

2、使用MATLAB代码实现灰度共生矩阵的计算

Gray=imread('.\I.jpg');    %输入灰度图像
[M,N,O] = size(Gray);
M = 128; 
N = 128;

%归一化,对原始灰度图像进行灰度值映射，这里将Gray量化成16级
for i = 1:M
      for j = 1:N
             for n = 1:256/16
                   if (n-1)*16<=Gray(i,j)&&Gray(i,j)<=(n-1)*16+15
                           Gray(i,j) = n-1;
                   end
             end
       end
end

%依照四种"相邻"条件计算四个共生矩阵P,取目标像素点对距离为1，角度分别为0°,45°,90°,135°
%计算后得到的P(m,n,4)就是四个共生矩阵构成的的三维数组
P = zeros(16,16,4);
for m = 1:16
      for n = 1:16
             for i = 1:M
                   for j = 1:N
                         if j1&&j

3、依据GLCM计算角二阶矩、熵、对比度、相关性
 

%需要使用上面求得的灰度共生矩阵P(m,n,4);如果嫌计算量太大,也可以对上面的GLCM再次归一化
H = zeros(1,4);
I = H;
Ux = H;       Uy = H;
deltaX= H;    deltaY = H;
C =H;
for n = 1:4
      E(n) = sum(sum(P(:,:,n).^2)); %能量
      for i = 1:16
             for j = 1:16
                  if P(i,j,n)~=0
                     H(n) = -P(i,j,n)*log(P(i,j,n))+H(n); %熵
                  end
                  I(n) = (i-j)^2*P(i,j,n)+I(n);%对比度

                   Ux(n) = i*P(i,j,n)+Ux(n); %相关性中μx
                   Uy(n) = j*P(i,j,n)+Uy(n); %相关性中μy
             end
       end
end
for n = 1:4
      for i = 1:16
            for j = 1:16
               deltaX(n) = (i-Ux(n))^2*P(i,j,n)+deltaX(n); %相关性中σx
               deltaY(n) = (j-Uy(n))^2*P(i,j,n)+deltaY(n); %相关性中σy
               C(n) = i*j*P(i,j,n)+C(n);
            end
      end
      C(n) = (C(n)-Ux(n)*Uy(n))/deltaX(n)/deltaY(n); %相关性
end

% 输出数据
sprintf('0,45,90,135方向上的能量依次为： %f, %f, %f, %f',E(1),E(2),E(3),E(4))
sprintf('0,45,90,135方向上的熵依次为： %f, %f, %f, %f',H(1),H(2),H(3),H(4))
sprintf('0,45,90,135方向上的惯性矩依次为： %f, %f, %f, %f',I(1),I(2),I(3),I(4))
sprintf('0,45,90,135方向上的相关性依次为： %f, %f, %f, %f',C(1),C(2),C(3),C(4))

五、总结

  因为最近在做图像的缺陷识别,所以接触到了灰度共生矩阵的计算和处理,读了几篇CSDN的博客,以及借助百度词条基本对这个陌生的名词有了一定的理解.限于本人知识水平,如有错误,望不吝赐教.

 

参考链接

[^1]: https://blog.csdn.net/guanyuqiu/article/details/53117507

[^2]: https://baike.baidu.com/item/%E7%81%B0%E5%BA%A6%E5%85%B1%E7%94%9F%E7%9F%A9%E9%98%B5/1498946?fr=aladdin#ref_[2]_4293543

[^3]: 名词释义参考自https://blog.csdn.net/guanyuqiu/article/details/53117507

[^4]: 参考自https://blog.csdn.net/lang_yubo/article/details/79151132

[^5]: “相邻”的含义参见上文“一、4、例证”第三段中内容