解题报告 (二) 强连通和2-sat
有向图强连通-算法详解
强连通分量题集
1)迷宫城堡
题意:给定N个点M条边(N <= 10000, M<= 100000),问是否存在任意的点对(i, j)使得i能够到j,并且j也能够到i。存在输出Yes,否则输出No。
题解:强连通分量的定义题。对原图求一次强连通,如果强连通分量为1,输出Yes,否则No。
2)Proving Equivalences
3)Equivalent Sets
题意:给定N个点M条边(N <= 20000, M<= 50000),问最少添加多少条边,使得该图的强连通分量为1。
题解:对原图求一次强连通,如果强连通分量个数已经为1,则不需要添加边;否则,进行缩图,缩完后的图统计两个量:入度为0的点的个数x,出度为0的点的个数y,需要添加的边数为max(x, y)。如图1所示,蓝色圈中的顶点属于同一个强连通分量,红色虚线代表需要添加的边。从图中可以看出需要添加的边只和入度为0或者出度为0的顶点有关。
图1
4)Intelligence System
题意:给定N个点M条边(N <= 50000, M<= 100000)的有向带权图,如果图中任意两点可达,则这两点之间的权为0。求从0号结点出发经过所有点的最小路径和。
题解:有向图强连通 + 最小生成树。首先求出强连通,然后对缩点后的图求一次最小生成树。注意是有向图,所以不能用Kruscal算法,只能用Prim求最小生成树。
5)Cactus
题意:给定N个点M条边(N <= 20000, M<= 50000)的有向图,如果这个图是一个强连通图,并且每条边属于一个环,则被称为Cactus,输出YES;否则NO。
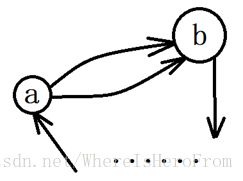
题解:有向图强连通 + BFS。首先求出强连通,如果连通分量个数大于1,直接输出NO;如果强连通分量为1,并且存在重边(如图2中的a->b),那么表明b经过一系列路径到达a的边一定属于至少两个环,输出NO;。
图2
然后枚举每条边未被标记的边
6)Summer Holiday
题意:给定N个人,M条关系(N <=1000, M<= 2000),,如果a到b有边则表示第a个人能够联系到第b个人,联系第i个人的花费为v[i],联系具有传递性。现在需要联系到所有人,求最小联系人数和最小花费。
题解:首先求出强连通分量,同一个连通分量中的人肯定取花费最小的那个人联系,这样整个连通分量的人都能联系到;将原图进行缩图,这样新图变成了一个有向无环图,那么必然存在一些点的入度为0,只要选择入度为0的这些点进行联系之后,其它人都可以通过传递性都联系到了。所以遍历新图找出入度为0的点累加该连通分量中的最小花费就是最后的答案了。
如图3所示,123所在强连通分量中选择花费最小的点以及4所在强连通分量(就是4本身)的最小化费之和就是最后的答案。
这题的详细解释参见文本引例:有向图强连通例题解析
图3
2-sat题集
1)Party
题意:有N(N <= 1000)对夫妻被邀请参加一个聚会,因为场地的问题,每对夫妻中只有1人可以列席。在2N个人中,某些人之间有着很大的矛盾(当然夫妻之间是没有矛盾的),有矛盾的2个人是不会同时出现在聚会上的。有没有可能会有N 个人同时列席?如果可能,输出YES,否则NO。
首先输入N和M(M<= 1000000);在接下来的M行中,每行会有4个数字,分别是 A1,A2, C1,C2,其中A1,A2分别表示是夫妻的编号;C1,C2 表示是妻子还是丈夫 ,0表示妻子 ,1是丈夫(夫妻编号从0到N -1 )。
题解:首先将每对夫妻看成是四个点,分别定义如下:
图4
其中i的取值为[0, N),所以总的结点数为4N。我们为了方便处理,将“不参加”的结点定义为偶数编号,将“参加”的结点定义为奇数编号;并且,妻子编号模4为(0,1),丈夫编号模4为(2, 3)。每个结点可以表示成如下通项:
![]()
图5
i代表第i对夫妻;j代表是妻子还是丈夫;k代表是否参加,这种编码方式的好处就是可以很方便的进行索引。
然后根据题中的关系,夫妻之间只有一人可以出席,并且需要N个人同时列席。也就是说需要满足四条关系式:
1.妻子不参加 => 丈夫必须参加;
2.妻子参加 => 丈夫必须不参加;
3.丈夫不参加 => 妻子必须参加;
4.丈夫参加 => 妻子必须不参加;
然后对于每对夫妻,建立如图所示的四条边:
图6
然后再来看M个条件:A1, A2, C1,C2,其中A1,A2分别表示夫妻的编号;C1,C2 表示是妻子还是丈夫 ,0表示妻子。这里隐含着四个结点:
Node(A1, C1, 0) 代表 第A1对夫妻中C1成员不参加;
Node(A1, C1, 1) 代表 第A1对夫妻中C1成员参加;
Node(A2, C2, 0) 代表 第A2对夫妻中C2成员不参加;
Node(A2, C2, 1) 代表 第A2对夫妻中C2成员参加;
因为(第A1对夫妻中C1成员)和(第A2对夫妻中C2成员)不能同时参加,则代表如果一个参加了,另一个必定不能参加。所以对这四个结点建立两条边,如下:
Node(A1, C1, 1) => Node(A2, C2, 0)
Node(A2, C2, 1) => Node(A1, C1, 0)
这样,所有的边建完后,总共就是4N个点,2M+4N条边,求一次强连通,然后遍历所有的结点,如果存在某个人“参加”和“不参加”代表的结点出现在同一个强连通分量中,说明他“参加”能够推导出“不参加”,“不参加”又能推导出“参加”,与事实矛盾,则输出NO,否则输出YES。
2)Wedding
题意:新娘,新郎和n对夫妇,分别坐在长条桌的两边,其中有m对人之间存在奸情(同性和异性皆有可能)。现在有两个限制:
1. 任意一对夫妇必须坐在长条桌的两面;
2. m对有奸情的人不能坐在新娘的对面;
求一种可能的方案,使得上面两种情况都能满足。
题解:对于第2种情况,有两种选择:第一种是将有奸情的人拆开坐到桌子的两面;第二种就是将他们和新娘坐在同一面。
将每个人拆成两个点i和i’,i代表坐左边,i’代表坐右边。定义每条边a=>b的含义为如果a坐左边,那么b也坐左边。那么这样约定以后,我们把新娘放到左边,做法就是 0h=>0w,即新郎到新娘连一条边,表示如果新郎坐左边,那么让新娘坐左边,让新郎坐右边去。对于每对奸情(a, b),建立两条边(a’=>b)和(b’=>a),即如果a坐右边,那么b必须坐左边;如果b坐右边,那么a必须坐左边。
然后求一次强连通,判断是否存在一对夫妻在同一个强连通分量中,如果存在,则上述坐法不存在。否则采用2-sat经典算法求一次拓扑排序即可。
3)Perfect Election
题意:N个候选人进行选举,需要满足M个条件(N <=1000,M <= 1000000),条件类型分为四种:
1. +i +j i和j至少一人被选中;
2. -i -j i和j至少一人不被选中;
3. +i -j i被选中 或 j不被选中;
4. -i +j i不被选中 或 j被选中;
问是否存在这样一种选举方式,满足所有M个条件。
题解:将每个人拆成两个点:i表示被选中,i’表示未被选中。以上四种情况都是两个人的选中和不选中的“或”:a or b。
a or b 等价于 (a’=>b) and (b’=>a)。每一个条件对应于两条边。其中a的取值为i或i’,b的取值为j或j’,代入等价式建立相应的边即可。然后求一次强连通,如果存在i和i’在同一个强连通分量,则与条件矛盾。
4)Katu Puzzle
题意:给定一些关系式a op b = c。其中op的取值为(AND, OR, XOR),a,b,c的取值为[0,1],其中a和b为未知数,给定未知数和关系式的个数,求是否存在这样一种解满足所有关系式,存在输出YES,否则NO。
题解:三种操作符×两种值,总共六种情况,把每个顶点X拆成两个点x和x’,分别代表1和0,然后分情况讨论:
1. a OR b = 1,这种是最经典的情况,建边:(a’=>b)和(b’=>a),含义是如果a为0,那么b必须为1,同样,如果b为0,那么a必须为1;
2. a OR b = 0,当且仅当a和b均为0时满足,所以建边(a=>a’)和(b=>b’),含义是无论如何a必须为0,b亦然;
3. a AND b = 1,当且仅当a和b均为1时满足,建边(a’=>a)和(b’=>b),含义和第2种情况正好相反;
4. a AND b = 0,建边(a=>b’)和(b=>a’),含义和第1种情况相反;
5. a XOR b = 1,这种情况需要建四条边,即a为0或1,b的情况;以及b为0或1时,a的情况;(a’=>b)、(b’=>a)、(a=>b’)和(b=>a’);
6. a XOR b = 0,参考第5种情况。
建完图后求一次强连通,如果存在两个点x和x’在同一个强连通分量中,说明无解,则输出NO,否则YES。
5)Priest John's BusiestDay
题意:给定N个时间段[Si, Ti]和对应的时间间隔Di,对于每个时间段可以选择[Si, Si+Di]或者[Ti-Di, Ti](即开始和结束)举行一个活动。问是否存在一种方案,使得N(N <= 1000)个活动都能举行(任意两个活动在时间上不能有交集)。
题解:将每个时间段拆成两个点:i表示[Si, Si+Di],i’表示[Ti-Di, Ti]。总共2000个点进行一次O(N^2)的区间两两判交。如果第i个时间区间和第j个时间区间有交集(边界重合不算),则建边(i=>j’),即第i个选的情况下,第j个不能选所以只能选j’。
然后求一次强连通,如果存在两个点i和i’在同一个强连通分量中,则输出NO;否则输出YES,然后采用2-sat对收缩后的反图求一次拓扑排序,输出路径。
需要注意一点,输出的时候需要对顶点进行排序,因为题目是Special Judge,它进行数据判定可行性的时候肯定是一一对应的去判的,所以需要输出的解也是排好序的。
6)Ikki's Story IV - Panda'sTrick
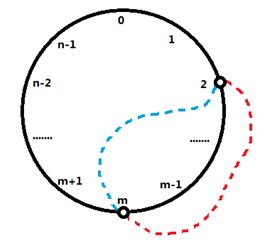
题意:一个圆上有n(n <= 1000)个结点,分别按顺序编号0,1,2…n-1,从圆上任意找两个点串起来,可以选择从圆里穿过(图7中蓝色虚线所示),也可以选择从圆外穿过(图7中红色虚线所示),每个结点只允许连一次。给定m对连接,问是否存在这样一种情况,所得所有连接之间互不相交。
图7
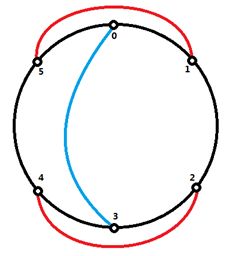
如图8,6个结点的情况,0<->3,1<->5,2<->4 连接的情况如下。
图8
题解:每个连接有两种情况,所以将每个连接拆成两个点x和x’,x代表蓝色连接,x’代表红色连接,然后就是判断圆内直线相交了,如果两个连接在圆内相交,那么说明他们不能同时用蓝色的连接方式,圆外亦然。所以如果两个连接相交,那么需要建立四条边,即:如果我选蓝,你就只能选红,等等。
(x=>y’)、(x’=>y)、(y=>x’)、(y’=>x),有点类似 XOR 的建边方式。
然后求一次强连通,如果存在两个点x和x’在同一个强连通分量中,则答案为NO;否则YES。
7)Get Luffy Out
题意:N(N <= 1024)对钥匙(Ai, Bi),M(M <= 2048)扇门,第i扇门用(Xi, Yi)表示,代表它只能由钥匙Xi或者钥匙Yi开启。
求用一种方案,从N对钥匙中取出N个钥匙(每对只能取一个),按顺序开门开启尽量多的门,求能够开启最多的门的个数。
题解:思路是这样的:首先要开启第i扇门必须先开启前i-1扇门,所以可以先二分一个需要开启的门的数量,对于第i扇门(Xi, Yi),如果Xi这个钥匙没有选,那么Yi这个钥匙必选;同样,如果Yi这个钥匙没选,那么Xi这个钥匙必选。
每个钥匙看成图的一个顶点,建好图后求强连通判可行即可。
8)Get Luffy Out *
题意:Get Luffy Out的加强版,每个钥匙有可能出现在不同的钥匙对中。
题解:首先还是二分答案。然后拆点,总共2N把钥匙,拆成4N个点,分别表示这个钥匙的取或不取。然后两种情况建边:
1.对于每对钥匙(x, y),如果x取,则y不取;同理,如果y取,则x不取;
2.对于每扇门(a, b),如果a不取,则b必须取;如果b不取,则a必须取;
9)Building roads(推荐)
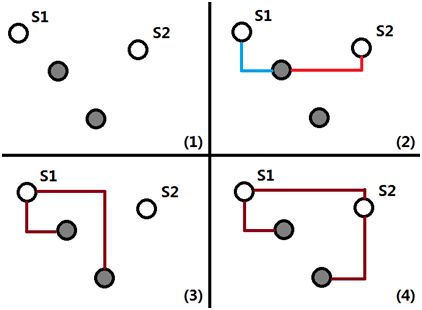
题意:如图9-(1),有两个中转点S1和S2,以及N(N <= 500)个灰色点,现在要求把灰色点和中转点连起来,每个灰色点要么连S1,要么连S2。如图9-(2),蓝色线连S1,红色线连S2,连接的距离定义为“曼哈顿距离”,两个灰色点之间的距离定义如下:
1.如果两个点连接的是同一个中转点,那么他们的距离为各自到中转点的距离之和,如图9-(3)所示;
2.如果两个点连接的不是同一个中转点,那么他们的距离为各自到中转点距离之和加上两个中转点之间的距离,如图9-(4)。
还有一些限制条件,给定一些灰色点必须连接到同一个中转点,以及一些灰色点必须连接到不同的中转点。
现在需要使得任意两个灰色结点之间的最大距离最小,求这个最大距离。
图9
题解:将每个灰色的点拆成两个点x和x’,x表示连接到S1,x’表示连接到S2。总共2N个结点,将距离计算出来预处理到数组dist[i][j],表示第i点和第j个点的距离(注意:这里的距离不是单纯的曼哈顿距离,需要算上分别连接到中转点的距离之和)。
然后二分一个距离d,如果dist[i][j] > d,则建边(i=>j’)和(j=>i’)。然后必须连接到同一个中转点的点对建四条边,必须连接到不同中转点的点对也建四条边。
然后强连通判可行即可。
10)Go Deeper
题意:给定这样一个递归的程序,其中x[n]数组为未知数,并且取值只有0或1;a[m]、b[m]、c[m]为给定数组,其中0 <= a[i], b[i] < n,0 <= c[i] <= 2,并且n<=200, m<=10000。求这个程序能够输出的最大的dep的值。
题解:虽然是个递归程序,但是它没有分叉,所以还是线性的。也就是一旦满足dep = m或者x[a[dep]] + x[b[dep]] == c[dep],函数就返回了。所以我们要做的就是将x[i]设置为合适的值,使得它能够满足的条件尽量多。
首先二分dep,考虑到x[i]只有0和1两种取值,所以可以把每个x[i]拆成两个分别代表0和1的点,然后根据c[j] (0<=j < dep)的值(0, 1, 2)分情况建边即可。建边方式可以参考Katu Puzzle。
建完边,求一次强连通分量,利用分拆的两个点是否在同一个强连通分量中来判定二分可行性。
11)Eliminate the Conflict
题意:题意围绕“剪刀石头布”而展开,给出Bob的N(N <=10^5)次出法(1代表石头、2代表纸、3代表剪刀),Alice需要满足M(M <= 10^5)个条件,条件分两种:
1、a b 0 第a次和第b次出法必须相同;
2、a b 1 第a次和第b次出法必须不同;
如果Alice在这N次对决中,没有一次输才算赢,问是否存在这样一种出法是的Alice获胜。
题解:Alice的每次出法都有两种选择:要么和Bob出的一样,要么赢过Bob;将这两种出法拆成两个点,总共2N个点,然后根据M个条件建立有向边。
1、 第a次和第b次出法必须相同,所以枚举第a次的两种情况和第b次的两种情况进行两两组合,如果出法不同则建边;
2、 第a次和第b次出法必须不同,所以枚举第a次的两种情况和第b次的两种情况进行两两组合,如果出法相同则建边;
建完边,求一次强连通判可行即可。
12)Bomb Game
题意:给定N组圆心(每组两个),要求选择N个圆心画圆(其中第2K和2K+1个不能同时选择),半径R可以由你控制,求最大的半径R使得所有圆不相交。
题解:首先,同一个组的圆分别记为圆i和圆i’。然后二分半径R,然后判断任意两个圆是否相交,如果圆i和圆j相交,则建两条边(i=>j’)和(j=>i’)。
建完边,求一次强连通判可行从而调整半径R。
13)Divide Groups
题意:给定一个N(N <= 100)个点的有向图,求能否将图分成两个“完全子图”(“完全子图”的定义为任意两个点都有边)。
题解:首先将原图的边关系存在邻接矩阵mat[i][j]中,mat[i][j]=1表示第i个点到第j个点有边;然后将每个点拆成两个点i和i’,分别表示属于两个子图。然后枚举任意两个顶点i, j,如果他们属于属于同一个子图,那么必须满足他们所代表的的原图中的点互相可达,如果不满足,则建边(i=>j’),代表i选了这个子图,那么j必须选另一个子图。
建完边求一次强连通,判可行即可。
14)Let's go home
题意:ACM集训队到了寒假需要回家过年,每一个队(三人一队)或者队长留下或者其余两名队员同时留下;每一对队员,如果队员A留下,则队员B必须回家休息下,或者B留下,A回家。求是否能满足这样的情况。
题解:比较裸的2-sat。总共三类边:
1、 对于每个队伍,队长回家,则其余两人必须同时留下;
2、 对于每个队伍,队员回家,则另一名队员也必须回家,队长必须留下;
3、 对于每对队员,A留下,则B回家;B留下,则A回家;
每个队员拆成两个点x代表回家,x’代表留下。按照上面三种规则建边即可。然后求一次强连通判断可行性。
15)Map Labeler
题意:二维平面上有N个点,每个点可以生成两个正方形,但是只能选择生成一个,并且该点需要位于正方形的“顶边中点”或“底边中点”。正方形的边长R可以随意控制,但是需要保证所有生成的正方形互不相交。求最大的边长R。
题解:首先二分边长R,然后按照规则生成所有的正方形总共2N个,第i组正方形编号分别为2i和2i+1,然后利用矩形判交把两两有交集的正方形建边。
求一次强连通判可行即可,类似Bomb Game。
16)Peaceful Commission
题意:N(N <= 8000)个党派要各自派1名代表参加一个会议,每个党派有两个代表,M(M <= 100000)对代表之间不喜欢对方,所以他们不能同时出现在会议上,问一种可行方案,使得所有党派都正好有一名代表参加会议,并且输出字典序最小的。
题解:2-sat建边后,从小到大枚举点选取。