常微分方程初值问题数值解法
常微分方程初值问题数值解法
一、问题提出
科学计算中经常遇到微分方程(组)初值问题,需要利用Euler法,改进Euler法,Rung-Kutta方法求其数值解,诸如以下问题:
(1)

(3)

(4)利用四阶标准R- K方法求二阶方程初值问题的数值解

二、问题分析
使用Euler法求解,运算程序简单,但是计算结果准确度不高。使用改进的Euler法求解过程相对复杂,但是准确度会更高。准确度最高的是四阶龙格库塔法,求解步骤也是最复杂的。问题(1)使用Euler求解,并与准确解对比。问题(3)使用改进的Euler法求解。问题(4)(I)(IV)使用四届标准龙格库塔法求解。
三、实验程序及注释
1.Euler法:
 View Code
View Code
//differential.cpp
#include <iostream>
using namespace std;
#include <math.h>
float h, //步长
x00, //x的取值范围
xn, // x0< x < xn
y00; //初值
float x[21];//结果
float y[21];
void Euler()
{
init();
x[0] = x00;
y[0] = y00;
for (int i=1; i<=(xn-x00)/h+1; i++)
{
x[i] = x[i-1] + h;
y[i] = y[i-1] + h * f(x[i-1],y[i-1]);
}
}
2.解问题(1):
 View Code
View Code
//常微分方程y’= f(xn,yn)
float f(float x, float y)
{
return 4*x/y-x*y;
//return y-2*x/y;//课本上的例题,由于检测程序的正确性
}
//初始化初值和x的范围
void init()
{
x00=0;
xn=2;
y00=3;
}
//求常微分方程的标准解
float pf(float x)
{
return sqrt(4+5*exp(-x*x));
}
int main()
{
h=0.1;
Euler();
cout << "步长 h = "
<< h << endl;
for (int i=1; i<=(xn-x00)/h+1; i++)
{
cout << "x" << i << "=" << x[i] << "\t"
<< "y" << i << "=" << y[i] << "\t"
<< "y("<< x[i] << ")=" << pf(x[i]) << endl;
}
h=0.2;
Euler();
cout << "步长 h = "
<< h << endl;
for (i=1; i<=(xn-x00)/h+1; i++)
{
cout << "x" << i << "=" << x[i] << "\t"
<< "y" << i << "=" << y[i] << "\t"
<< "y("<< x[i] << ")=" << pf(x[i]) << endl;
}
h=0.4;
Euler();
cout << "步长 h = "
<< h << endl;
for (i=1; i<=(xn-x00)/h+1; i++)
{
cout << "x" << i << "=" << x[i] << "\t"
<< "y" << i << "=" << y[i] << "\t"
<< "y("<< x[i] << ")=" << pf(x[i]) << endl;
}
return 0;
}
3.改进的Euler法:
 View Code
View Code
#include <iostream>
#include <iomanip>
using namespace std;
float h, //步长
x00, //x的取值范围
xn, // x0< x < xn
y00; //初值
float y10,y20,y30;//初值
float x[21];//结果
float y1[21],y2[21],y3[21];
//改进的Euler法
void newEuler()
{
init();
x[0] = x00;
y1[0] = y10;
y2[0] = y20;
y3[0] = y30;
for (int i=1; i<=(xn-x00)/h+1; i++)
{
x[i] = x[i-1] + h;
float yp=y1[i-1]+h*f1(x[i-1],y1[i-1],y2[i-1],y3[i-1]);
float yc=y1[i-1]+h*f1(x[i],yp,y2[i-1],y3[i-1]);
y1[i] = 0.5*(yp+yc);
yp=y2[i-1]+h*f2(x[i-1],y1[i-1],y2[i-1],y3[i-1]);
yc=y2[i-1]+h*f2(x[i],y1[i-1],yp,y3[i-1]);
y2[i] = 0.5*(yp+yc);
yp=y3[i-1]+h*f3(x[i-1],y1[i-1],y2[i-1],y3[i-1]);
yc=y3[i-1]+h*f3(x[i],y1[i-1],y2[i-1],yp);
y3[i] = 0.5*(yp+yc);
}
}
4.解问题(3):
 View Code
View Code
float f1(float x, float y1, float y2, float y3)
{
return y2;
}
float f2(float x, float y1, float y2, float y3)
{
return -y1;
}
float f3(float x, float y1, float y2, float y3)
{
return -y3;
}
void init()
{
x00=0;
xn=0.15;
y10=-1;
y20=0;
y30=1;
}
int main()
{
h=0.01;
newEuler();
cout << "步长 h = "
<< h << endl;
cout.precision(6);
for (int i=0; i<=(xn-x00)/h; i+=5)
{
cout << "x(" << setw(2) << i << ")=" << x[i] << ""
<< "y1(" << setw(2) << x[i] << ")=" << y1[i] << ""
<< "y2(" << setw(2) << x[i] << ")=" << y2[i] << ""
<< "y3(" << setw(2) << x[i] << ")=" << y3[i] << endl;
}
return 0;
}
5.龙格库塔法:
 View Code
View Code
#include <iostream>
#include <iomanip>
using namespace std;
float h, //步长
x00, //x的取值范围
xn; // x0< x < xn
float y10;
float y20;//初值
float x[51];//结果
float y1[51],y2[51];
//龙格库塔法
void L_k()
{
float L[5];
init();
x[0]=x00;
y1[0]=y10;
y2[0]=y20;
for (int i=1; i<=(xn-x00)/h; i++)
{
x[i] = x[i-1] + h;
L[1] = f2(x[i-1],y1[i-1],y2[i-1]);
L[2] = f2(x[i-1]+h/2,y1[i-1]+h*y2[i-1]/2,y2[i-1]+h*L[1]/2);
L[3] = f2(x[i-1]+h/2,y1[i-1]+h*y2[i-1]/2+h*h*L[1]/4,y2[i-1]+h*L[2]/2);
L[4] = f2(x[i-1]+h,y1[i-1]+h*y2[i-1]+h*h*L[2]/2,y2[i-1]+h*L[3]);
y1[i] = y1[i-1] + h*y2[i-1] + h*h*(L[1]+L[2]+L[3])/6;
y2[i] = y2[i-1] + h*(L[1]+2*L[2]+2*L[3]+L[4])/6;
}
}
6.解问题(4)(I):
 View Code
View Code
// y1'=y2
// y2'=3*y2-*y1
float f1(float x, float y1, float y2)
{
return y2;
}
float f2(float x, float y1, float y2)
{
return 3*y2-2*y1;
}
void init()
{
x00=0;
xn=1;
y10=0;
y20=1;
}
int main()
{
h=0.02;
L_k();
cout << "步长 h = "
<< h << endl;
cout.precision(6);
for (int i=0; i<=(xn-x00)/h; i++)
{
cout << "x(" << setw(2) << i << ")=" << x[i] << ""
<< "y1(" << setw(2) << x[i] << ")=" << y1[i] << ""
<< "y2(" << setw(2) << x[i] << ")=" << y2[i] << endl;
}
return 0;
}
7.解问题(4)(IV):
 View Code
View Code
// y1'=y2
// y2'=-sin(y1)
float f1(float x, float y1, float y2)
{
return y2;
}
float f2(float x, float y1, float y2)
{
return -sin(y1);
}
void init()
{
x00=0;
xn=4;
y10=1;
y20=0;
}
int main()
{
h=0.2;
L_k();
……
……
return 0;
}
四、实验数据结果及分析
1.解问题(1):
Euler法
步长 h = 0.1
x1=0.1 y1=3 y(0.1)=2.9917
x2=0.2 y2=2.98333 y(0.2)=2.96714
x3=0.3 y3=2.95048 y(0.3)=2.9274
x4=0.4 y4=2.90264 y(0.4)=2.87415
x5=0.5 y5=2.84166 y(0.5)=2.80963
x6=0.6 y6=2.76995 y(0.6)=2.73649
x7=0.7 y7=2.6904 y(0.7)=2.65766
x8=0.8 y8=2.60615 y(0.8)=2.57613
x9=0.9 y9=2.52044 y(0.9)=2.49485
x10=1 y10=2.43643 y(1)=2.41648
x11=1.1 y11=2.35697 y(1.1)=2.34329
x12=1.2 y12=2.28438 y(1.2)=2.27698
x13=1.3 y13=2.22038 y(1.3)=2.21869
x14=1.4 y14=2.16592 y(1.4)=2.16894
x15=1.5 y15=2.12124 y(1.5)=2.12767
x16=1.6 y16=2.08591 y(1.6)=2.0944
x17=1.7 y17=2.05898 y(1.7)=2.0683
x18=1.8 y18=2.03922 y(1.8)=2.04837
x19=1.9 y19=2.02523 y(1.9)=2.03353
x20=2 y20=2.01571 y(2)=2.02276
步长 h = 0.2
x1=0.2 y1=3 y(0.2)=2.96714
x2=0.4 y2=2.93333 y(0.4)=2.87415
x3=0.6 y3=2.80776 y(0.6)=2.73649
x4=0.8 y4=2.64178 y(0.8)=2.57613
x5=1 y5=2.46136 y(1)=2.41648
x6=1.2 y6=2.29411 y(1.2)=2.27698
x7=1.4 y7=2.16199 y(1.4)=2.16894
x8=1.6 y8=2.07467 y(1.6)=2.0944
x9=1.8 y9=2.02774 y(1.8)=2.04837
x10=2 y10=2.0079 y(2)=2.02276
步长 h = 0.4
x1=0.4 y1=3 y(0.4)=2.87415
x2=0.8 y2=2.73333 y(0.8)=2.57613
x3=1.2 y3=2.32696 y(1.2)=2.27698
x4=1.6 y4=2.03513 y(1.6)=2.0944
x5=2 y5=1.99055 y(2)=2.02276
2.解问题(3):
步长 h = 0.01
x( 0)=0 y1( 0)=-1 y2( 0)=0 y3( 0)=1
x( 5)=0.05 y1(0.05)=-0.999 y2(0.05)=0.04999 y3(0.05)=0.95123
x(10)=0.1 y1(0.1)=-0.995502 y2(0.1)=0.09988 y3(0.1)=0.904839
x(15)=0.15 y1(0.15)=-0.989514 y2(0.15)=0.149545 y3(0.15)=0.86071
参考结果:
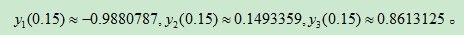
对比看,结果相差不大,参考结果应该是使用四阶龙格库塔方法求解的。
3.解问题(4)(I):
步长 h = 0.02
x( 0)=0 y1( 0)=0 y2( 0)=1
x( 1)=0.02 y1(0.02)=0.0206094 y2(0.02)=1.06142
x( 2)=0.04 y1(0.04)=0.0424763 y2(0.04)=1.12576
x( 3)=0.06 y1(0.06)=0.0656603 y2(0.06)=1.19316
x( 4)=0.08 y1(0.08)=0.0902238 y2(0.08)=1.26373
x( 5)=0.1 y1(0.1)=0.116232 y2(0.1)=1.33763
x( 6)=0.12 y1(0.12)=0.143752 y2(0.12)=1.415
x( 7)=0.14 y1(0.14)=0.172856 y2(0.14)=1.49599
x( 8)=0.16 y1(0.16)=0.203617 y2(0.16)=1.58074
x( 9)=0.18 y1(0.18)=0.236112 y2(0.18)=1.66944
x(10)=0.2 y1(0.2)=0.270422 y2(0.2)=1.76225
x(11)=0.22 y1(0.22)=0.30663 y2(0.22)=1.85934
x(12)=0.24 y1(0.24)=0.344825 y2(0.24)=1.9609
x(13)=0.26 y1(0.26)=0.385097 y2(0.26)=2.06712
x(14)=0.28 y1(0.28)=0.427543 y2(0.28)=2.17821
x(15)=0.3 y1(0.3)=0.47226 y2(0.3)=2.29438
x(16)=0.32 y1(0.32)=0.519353 y2(0.32)=2.41583
x(17)=0.34 y1(0.34)=0.56893 y2(0.34)=2.54281
x(18)=0.36 y1(0.36)=0.621104 y2(0.36)=2.67554
x(19)=0.38 y1(0.38)=0.675991 y2(0.38)=2.81427
x(20)=0.4 y1(0.4)=0.733716 y2(0.4)=2.95926
x(21)=0.42 y1(0.42)=0.794405 y2(0.42)=3.11077
x(22)=0.44 y1(0.44)=0.858192 y2(0.44)=3.26909
x(23)=0.46 y1(0.46)=0.925216 y2(0.46)=3.43451
x(24)=0.48 y1(0.48)=0.995622 y2(0.48)=3.60732
x(25)=0.5 y1(0.5)=1.06956 y2(0.5)=3.78784
x(26)=0.52 y1(0.52)=1.14719 y2(0.52)=3.97641
x(27)=0.54 y1(0.54)=1.22867 y2(0.54)=4.17335
x(28)=0.56 y1(0.56)=1.31418 y2(0.56)=4.37903
x(29)=0.58 y1(0.58)=1.40389 y2(0.58)=4.59383
x(30)=0.6 y1(0.6)=1.498 y2(0.6)=4.81811
x(31)=0.62 y1(0.62)=1.59668 y2(0.62)=5.0523
x(32)=0.64 y1(0.64)=1.70016 y2(0.64)=5.2968
x(33)=0.66 y1(0.66)=1.80863 y2(0.66)=5.55205
x(34)=0.68 y1(0.68)=1.92232 y2(0.68)=5.81851
x(35)=0.7 y1(0.7)=2.04145 y2(0.7)=6.09665
x(36)=0.72 y1(0.72)=2.16626 y2(0.72)=6.38696
x(37)=0.74 y1(0.74)=2.29701 y2(0.74)=6.68996
x(38)=0.76 y1(0.76)=2.43395 y2(0.76)=7.00617
x(39)=0.78 y1(0.78)=2.57735 y2(0.78)=7.33617
x(40)=0.8 y1(0.8)=2.72749 y2(0.8)=7.68052
x(41)=0.82 y1(0.82)=2.88467 y2(0.82)=8.03984
x(42)=0.84 y1(0.84)=3.04919 y2(0.84)=8.41474
x(43)=0.86 y1(0.86)=3.22137 y2(0.86)=8.8059
x(44)=0.88 y1(0.88)=3.40154 y2(0.88)=9.21397
x(45)=0.9 y1(0.9)=3.59004 y2(0.9)=9.63969
x(46)=0.92 y1(0.92)=3.78725 y2(0.92)=10.0838
x(47)=0.94 y1(0.94)=3.99352 y2(0.94)=10.547
x(48)=0.96 y1(0.96)=4.20926 y2(0.96)=11.0302
x(49)=0.98 y1(0.98)=4.43487 y2(0.98)=11.5342
x(50)=1 y1( 1)=4.67077 y2( 1)=12.0598
3.解问题(4)(IV):
步长 h = 0.2
x( 0)=0 y1( 0)=1 y2( 0)=0
x( 1)=0.2 y1(0.2)=0.983201 y2(0.2)=-0.167682
x( 2)=0.4 y1(0.4)=0.933176 y2(0.4)=-0.331607
x( 3)=0.6 y1(0.6)=0.851087 y2(0.6)=-0.48757
x( 4)=0.8 y1(0.8)=0.739008 y2(0.8)=-0.630607
x( 5)=1 y1( 1)=0.60009 y2( 1)=-0.754957
x( 6)=1.2 y1(1.2)=0.438688 y2(1.2)=-0.854407
x( 7)=1.4 y1(1.4)=0.260389 y2(1.4)=-0.923023
x( 8)=1.6 y1(1.6)=0.0718545 y2(1.6)=-0.956155
x( 9)=1.8 y1(1.8)=-0.119534 y2(1.8)=-0.951378
x(10)=2 y1( 2)=-0.306182 y2( 2)=-0.90905
x(11)=2.2 y1(2.2)=-0.480844 y2(2.2)=-0.832224
x(12)=2.4 y1(2.4)=-0.637103 y2(2.4)=-0.725968
x(13)=2.6 y1(2.6)=-0.769673 y2(2.6)=-0.596373
x(14)=2.8 y1(2.8)=-0.874507 y2(2.8)=-0.449594
x(15)=3 y1( 3)=-0.948738 y2( 3)=-0.291209
x(16)=3.2 y1(3.2)=-0.990535 y2(3.2)=-0.125976
x(17)=3.4 y1(3.4)=-0.998943 y2(3.4)=0.0420493
x(18)=3.6 y1(3.6)=-0.973777 y2(3.6)=0.209154
x(19)=3.8 y1(3.8)=-0.915597 y2(3.8)=0.371509
x(20)=4 y1( 4)=-0.825779 y2( 4)=0.524739
五、实验结论
使用c语言写代码虽然比Matlab的代码长,但是还是c语言适合用来做练习,因为用c写更有结构。Matlab隐藏了许多细节部分,不适合对方法的深入理解,但是写代码速度快,代码更简练。
