机器学习-白板推导系列笔记(二十四)-直面配分函数
此文章主要是结合哔站shuhuai008大佬的白板推导视频:直面配分函数_134min
全部笔记的汇总贴:机器学习-白板推导系列笔记
直面配分函数-对应花书第十八章
动机:Learning问题、evaluation问题
一、对数似然梯度
x ∈ R p , { 0 , 1 } p x\in \R^p,\{0,1\}^p x∈Rp,{ 0,1}p
许多概率图模型(通常无向图模型),由一个为归一化的 p ^ ( x ; θ ) \hat p(x;\theta) p^(x;θ)定义,我们必须除以一个配分函数 Z ( θ ) Z(\theta) Z(θ)来归一化, p ( x ; θ ) = 1 Z ( θ ) p ^ ( x ; θ ) p(x;\theta)=\frac1{Z(\theta)} \hat p(x;\theta) p(x;θ)=Z(θ)1p^(x;θ)
配分函数 Z ( θ ) Z(\theta) Z(θ)是对未归一化概率所有状态的积分或者求和:
Z ( θ ) = ∫ p ^ ( x ) d x o r Z ( θ ) = ∑ x p ^ ( x ) Z(\theta)=\int \hat p(x){d}x\;\;\;\;\;or\;\;\;\;\;\;Z(\theta)=\sum_x\hat p(x) Z(θ)=∫p^(x)dxorZ(θ)=x∑p^(x)
ML learning:Given X = { x i } i = 1 N , e s t i m a t e : θ X=\{x_i\}^N_{i=1},estimate:\theta X={ xi}i=1N,estimate:θ
θ = arg max θ p ( x ; θ ) = arg max θ ∏ i = 1 N p ( x i ; θ ) \theta=\underset{\theta}{\argmax }p(x;\theta)=\underset{\theta}{\argmax}\prod^N_{i=1}p(x_i;\theta) θ=θargmaxp(x;θ)=θargmaxi=1∏Np(xi;θ)
引入一个 log \log log
θ = arg max θ log ∏ i = 1 N p ( x i ; θ ) = arg max θ ∑ i = 1 N log p ( x i ; θ ) = arg max θ ∑ i = 1 N ( log p ^ ( x i ; θ ) − log Z ( θ ) ) = arg max θ ∑ i = 1 N log p ^ ( x i ; θ ) − N ⋅ log Z ( θ ) = arg max θ 1 N ∑ i = 1 N log p ^ ( x i ; θ ) − log Z ( θ ) ( 提 一 个 N 对 计 算 无 影 响 ) \theta=\underset{\theta}{\argmax}\log\prod^N_{i=1}p(x_i;\theta)\\=\underset{\theta}{\argmax}\sum^N_{i=1}\log p(x_i;\theta)\\=\underset{\theta}{\argmax}\sum^N_{i=1}(\log \hat p(x_i;\theta)-\log Z(\theta))\\=\underset{\theta}{\argmax}\sum^N_{i=1}\log \hat p(x_i;\theta)-N\cdot\log Z(\theta)\\=\underset{\theta}{\argmax}\frac1N\sum^N_{i=1}\log \hat p(x_i;\theta)-\log Z(\theta)\\(提一个N对计算无影响) θ=θargmaxlogi=1∏Np(xi;θ)=θargmaxi=1∑Nlogp(xi;θ)=θargmaxi=1∑N(logp^(xi;θ)−logZ(θ))=θargmaxi=1∑Nlogp^(xi;θ)−N⋅logZ(θ)=θargmaxN1i=1∑Nlogp^(xi;θ)−logZ(θ)(提一个N对计算无影响)
l ( θ ) = 1 N ∑ i = 1 N log p ^ ( x i ; θ ) − log Z ( θ ) l(\theta)=\frac1N\sum^N_{i=1}\log \hat p(x_i;\theta)-\log Z(\theta) l(θ)=N1i=1∑Nlogp^(xi;θ)−logZ(θ)
求梯度,
∇ θ l ( θ ) = 1 N ∑ i = 1 N ∇ θ log p ^ ( x i ; θ ) − ∇ θ log Z ( θ ) \nabla_\theta l(\theta)=\frac1N\sum^N_{i=1}\nabla_\theta\log \hat p(x_i;\theta)-\nabla_\theta\log Z(\theta) ∇θl(θ)=N1i=1∑N∇θlogp^(xi;θ)−∇θlogZ(θ)
∇ θ log Z ( θ ) = 1 Z ( θ ) ∇ θ Z ( θ ) = p ( x ; θ ) p ^ ( x ; θ ) ∇ θ ∫ p ^ ( x ) d x = p ( x ; θ ) p ^ ( x ; θ ) ∫ ∇ θ p ^ ( x ) d x = ∫ p ( x ; θ ) p ^ ( x ; θ ) ∇ θ p ^ ( x ) d x = ∫ p ( x ; θ ) ∇ θ log p ^ ( x ) d x = E p ( x ; θ ) [ ∇ θ log p ^ ( x ) ] \nabla_\theta\log Z(\theta)=\frac1{Z(\theta)}\nabla_\theta Z(\theta)\\=\frac{p(x;\theta)}{\hat p(x;\theta)}\nabla_\theta \int \hat p(x){d}x\\=\frac{p(x;\theta)}{\hat p(x;\theta)}\int\nabla_\theta \hat p(x){d}x\\=\int\frac{p(x;\theta)}{\hat p(x;\theta)}\nabla_\theta \hat p(x){d}x\\=\int{p(x;\theta)}\nabla_\theta \log \hat p(x){d}x\\=E_{p(x;\theta)}[\nabla_\theta \log \hat p(x)] ∇θlogZ(θ)=Z(θ)1∇θZ(θ)=p^(x;θ)p(x;θ)∇θ∫p^(x)dx=p^(x;θ)p(x;θ)∫∇θp^(x)dx=∫p^(x;θ)p(x;θ)∇θp^(x)dx=∫p(x;θ)∇θlogp^(x)dx=Ep(x;θ)[∇θlogp^(x)]
二、随机最大似然
∇ θ l ( θ ) = 1 N ∑ i = 1 N ∇ θ log p ^ ( x i ; θ ) − E p ( x ; θ ) [ ∇ θ log p ^ ( x ; θ ) ] = E P d a t a [ ∇ θ log p ^ ( x ; θ ) ] ⏟ p o s t i v e p h a s e − E P m o d e l [ ∇ θ log p ^ ( x ; θ ) ] ⏟ n e g a t i v e p h a s e \nabla_\theta l(\theta)=\frac1N\sum^N_{i=1}\nabla_\theta\log \hat p(x_i;\theta)-E_{p(x;\theta)}[\nabla_\theta \log \hat p(x;\theta)]\\=\underset{postive\;phase}{\underbrace{E_{P_{data}}[\nabla_\theta\log \hat p(x;\theta)]}}-\underset{negative\;phase}{\underbrace{E_{P_{model}}[\nabla_\theta \log \hat p(x;\theta)]}} ∇θl(θ)=N1i=1∑N∇θlogp^(xi;θ)−Ep(x;θ)[∇θlogp^(x;θ)]=postivephase EPdata[∇θlogp^(x;θ)]−negativephase EPmodel[∇θlogp^(x;θ)]
{ d a t a d i s t r o b u t i o n : P d a t a m o d e l d i s t r i b u t i o n : P m o d e l = Δ P ( x ; θ ) \left\{\begin{matrix} data\;distrobution:P_{data}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\model\;distribution :P_{model}\overset{\Delta}{=} P(x;\theta) \end{matrix}\right. { datadistrobution:Pdatamodeldistribution:Pmodel=ΔP(x;θ)
Gradient Ascend:
θ ( t + 1 ) = θ ( t ) + η ∇ θ ( l θ ( t ) ) \theta^{(t+1)}=\theta^{(t)}+\eta\nabla_\theta(l_\theta^{(t)}) θ(t+1)=θ(t)+η∇θ(lθ(t))
Gibbs Sampling from P m o d e l = P ( x ; θ ( t ) ) , { x ^ i } i = 1 m P_{model}{=} P(x;\theta^{(t)}),\{\hat x_i\}^m_{i=1} Pmodel=P(x;θ(t)),{ x^i}i=1m
x ^ 1 ∼ P ( x ; θ ( t ) ) x ^ 2 ∼ P ( x ; θ ( t ) ) ⋮ x ^ m ∼ P ( x ; θ ( t ) ) } → f a n t a c y p a r t i c l e s \left.\begin{matrix} \hat x_1\sim P(x;\theta^{(t)})\\\hat x_2\sim P(x;\theta^{(t)})\\\vdots\\\hat x_m\sim P(x;\theta^{(t)}) \end{matrix}\right\}\rightarrow fantacy\;particles x^1∼P(x;θ(t))x^2∼P(x;θ(t))⋮x^m∼P(x;θ(t))⎭⎪⎪⎪⎬⎪⎪⎪⎫→fantacyparticles
所以,Gradient Ascend based on MCMC:
θ ( t + 1 ) = θ ( t ) + η ( ∑ i = 1 m ∇ θ log p ^ ( x i ; θ ( t ) ) − ∑ i = 1 m ∇ θ log p ^ ( x ^ i ; θ ( t ) ) ) \theta^{(t+1)}=\theta^{(t)}+\eta(\sum^m_{i=1}\nabla_\theta\log \hat p(x_i;\theta^{(t)})-\sum^m_{i=1}\nabla_\theta\log \hat p(\hat x_i;\theta^{(t)})) θ(t+1)=θ(t)+η(i=1∑m∇θlogp^(xi;θ(t))−i=1∑m∇θlogp^(x^i;θ(t)))
三、对比散度
Gibbs采样时采用空间换时间,每一个需要 k − s t e p k-step k−step,这个k可能是极大的,所以我们需要采用对比散度的方法,使初始化马尔科夫链为采样自数据分布中的样本,可以大大降低混合时间(mixing time)。
CD-k(k= 1 , 2 , ⋯ 1,2,\cdots 1,2,⋯):
x ^ i = x i ( x i 为 t r a i n i n g d a t a , 是 从 P d a t a 中 采 样 得 到 的 ) \hat x_i=x_i(x_i为training\;data,是从P_{data}中采样得到的) x^i=xi(xi为trainingdata,是从Pdata中采样得到的)
θ ^ = arg min θ ( K L ( P ( 0 ) ∣ P ( ∞ ) ) − K L ( P ( k ) ∣ P ( ∞ ) ) ⏟ C o n t r a s t i v e D i v e r g e n c e ) \hat\theta=\underset{\theta}{\argmin}\Big(\underset{Contrastive\;Divergence}{\underbrace{KL(P^{(0)}|P^{(\infty)})-KL(P^{(k)}|P^{(\infty)})}}\Big) θ^=θargmin(ContrastiveDivergence KL(P(0)∣P(∞))−KL(P(k)∣P(∞)))极大似然估计:
θ ^ = arg max θ 1 N ∑ i = 1 N log p ( x i ; θ ) = arg max θ E P d a t a [ log P m o d e l ( x ; θ ) ] = arg max θ ∫ P d a t a log P m o d e l ( x ; θ ) d x = P d a t a 与 θ 无 关 arg max θ ∫ P d a t a log P m o d e l ( x ; θ ) P d a t a d x = arg max θ − K L ( P d a t a ∣ P m o d e l ( x ; θ ) ) = arg min θ K L ( P d a t a ∣ P m o d e l ( x ; θ ) ) = arg min θ K L ( P ( 0 ) ∣ P ( ∞ ) ) \hat\theta=\underset{\theta}{\argmax}\frac1N\sum^N_{i=1}\log p(x_i;\theta)\\=\underset{\theta}{\argmax}E_{P_{data}}[\log P_{model}(x;\theta)]\\=\underset{\theta}{\argmax}\int{P_{data}}\log P_{model}(x;\theta){d}x\\\overset{P_{data}与\theta无关}{=}\underset{\theta}{\argmax}\int{P_{data}}\log \frac{P_{model}(x;\theta)}{P_{data}}{d}x\\=\underset{\theta}{\argmax}-KL(P_{data}|P_{model}(x;\theta))\\=\underset{\theta}{\argmin}KL(P_{data}|P_{model}(x;\theta))\\=\underset{\theta}{\argmin}KL(P^{(0)}|P^{(\infty)}) θ^=θargmaxN1i=1∑Nlogp(xi;θ)=θargmaxEPdata[logPmodel(x;θ)]=θargmax∫PdatalogPmodel(x;θ)dx=Pdata与θ无关θargmax∫PdatalogPdataPmodel(x;θ)dx=θargmax−KL(Pdata∣Pmodel(x;θ))=θargminKL(Pdata∣Pmodel(x;θ))=θargminKL(P(0)∣P(∞))
四、RBM的Learning问题
x = ( x 1 x 2 ⋮ x p ) = ( h v ) h = ( h 1 h 2 ⋮ h m ) v = ( v 1 v 2 ⋮ v n ) p = m + n x=\left(\begin{matrix} x_1\\x_2\\\vdots\\x_p\end{matrix}\right )=\left(\begin{matrix} h\\v\end{matrix}\right )\;\;h=\left(\begin{matrix} h_1\\h_2\\\vdots\\h_m\end{matrix}\right )\;\;v=\left(\begin{matrix} v_1\\v_2\\\vdots\\v_n\end{matrix}\right )\;\;p=m+n x=⎝⎜⎜⎜⎛x1x2⋮xp⎠⎟⎟⎟⎞=(hv)h=⎝⎜⎜⎜⎛h1h2⋮hm⎠⎟⎟⎟⎞v=⎝⎜⎜⎜⎛v1v2⋮vn⎠⎟⎟⎟⎞p=m+n
W = [ w i j ] m ∗ n α = ( α 1 α 2 ⋮ α n ) β = ( β 1 β 2 ⋮ β m ) W=[w_{ij}]_{m*n}\;\;\alpha=\left(\begin{matrix} \alpha_1\\\alpha_2\\\vdots\\\alpha_n\end{matrix}\right )\;\;\beta=\left(\begin{matrix} \beta_1\\\beta_2\\\vdots\\\beta_m\end{matrix}\right ) W=[wij]m∗nα=⎝⎜⎜⎜⎛α1α2⋮αn⎠⎟⎟⎟⎞β=⎝⎜⎜⎜⎛β1β2⋮βm⎠⎟⎟⎟⎞
{ P ( x ) = 1 Z exp { − E ( h , v ) } E ( h , v ) = − ( h T W v + α T v + β T h ) \left\{\begin{matrix} P(x)=\frac1Z\exp\{-E(h,v)\}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \\E(h,v)=-(h^TWv+\alpha^T v+\beta^T h) \end{matrix}\right. ⎩⎨⎧P(x)=Z1exp{ −E(h,v)}E(h,v)=−(hTWv+αTv+βTh)
log-likelihood:
training set V ∈ S , ∣ S ∣ = N V\in S,|S|=N V∈S,∣S∣=N
1 N ∑ V ∈ S log P ( V ) \frac1N\sum_{V\in S}\log P(V) N1V∈S∑logP(V)
log-likelihood gradient:
∂ ∂ θ 1 N ∑ V ∈ S log P ( V ) \frac{\partial}{\partial\theta}\frac1N\sum_{V\in S}\log P(V) ∂θ∂N1V∈S∑logP(V)
所以,
log P ( V ) = log ∑ h P ( h , v ) = log ∑ h 1 Z exp { − E ( h , v ) } = log ∑ h exp { − E ( h , v ) } ⏟ ① − log ∑ h , v exp { − E ( h , v ) } ⏟ ② \log P(V)=\log\sum_hP(h,v)\\=\log\sum_h\frac1Z\exp\{-E(h,v)\}\\=\underset{①}{\underbrace{\log\sum_h\exp\{-E(h,v)\}}}-\underset{②}{\underbrace{\log\sum_{h,v}\exp\{-E(h,v)\}}} logP(V)=logh∑P(h,v)=logh∑Z1exp{ −E(h,v)}=① logh∑exp{ −E(h,v)}−② logh,v∑exp{ −E(h,v)}
∂ ∂ θ log P ( V ) = ∂ ∂ θ ① − ∂ ∂ θ ② \frac{\partial}{\partial\theta}\log P(V)=\frac{\partial}{\partial\theta}①-\frac{\partial}{\partial\theta}② ∂θ∂logP(V)=∂θ∂①−∂θ∂②
∂ ∂ θ ① = ∂ ∂ θ log ∑ h exp { − E ( h , v ) } = − 1 ∑ h exp { − E ( h , v ) } ∑ h exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h exp { − E ( h , v ) } ∑ h exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h 1 Z exp { − E ( h , v ) } 1 Z ∑ h exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h P ( h ∣ v ) ⋅ ∂ E ( h , v ) ∂ θ \frac{\partial}{\partial\theta}①=\frac{\partial}{\partial\theta}\log\sum_h\exp\{-E(h,v)\}\\=-\frac1{\sum_h\exp\{-E(h,v)\}}\sum_h\exp\{-E(h,v)\}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_h\frac{\exp\{-E(h,v)\}}{\sum_h\exp\{-E(h,v)\}}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_h\frac{\frac1Z\exp\{-E(h,v)\}}{\frac1Z\sum_h\exp\{-E(h,v)\}}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_hP(h|v)\cdot\frac{\partial E(h,v)}{\partial\theta} ∂θ∂①=∂θ∂logh∑exp{ −E(h,v)}=−∑hexp{ −E(h,v)}1h∑exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h∑∑hexp{ −E(h,v)}exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h∑Z1∑hexp{ −E(h,v)}Z1exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h∑P(h∣v)⋅∂θ∂E(h,v)
∂ ∂ θ ② = ∂ ∂ θ log ∑ h , v exp { − E ( h , v ) } = − 1 ∑ h , v exp { − E ( h , v ) } ∑ h , v exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h , v exp { − E ( h , v ) } ∑ h , v exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h , v 1 Z exp { − E ( h , v ) } 1 Z ∑ h , v exp { − E ( h , v ) } ⋅ ∂ E ( h , v ) ∂ θ = − ∑ h , v P ( h , v ) ⋅ ∂ E ( h , v ) ∂ θ \frac{\partial}{\partial\theta}②=\frac{\partial}{\partial\theta}\log\sum_{h,v}\exp\{-E(h,v)\}\\=-\frac1{\sum_{h,v}\exp\{-E(h,v)\}}\sum_{h,v}\exp\{-E(h,v)\}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_{h,v}\frac{\exp\{-E(h,v)\}}{\sum_{h,v}\exp\{-E(h,v)\}}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_{h,v}\frac{\frac1Z\exp\{-E(h,v)\}}{\frac1Z\sum_{h,v}\exp\{-E(h,v)\}}\cdot\frac{\partial E(h,v)}{\partial\theta}\\=-\sum_{h,v}P(h,v)\cdot\frac{\partial E(h,v)}{\partial\theta} ∂θ∂②=∂θ∂logh,v∑exp{ −E(h,v)}=−∑h,vexp{ −E(h,v)}1h,v∑exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h,v∑∑h,vexp{ −E(h,v)}exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h,v∑Z1∑h,vexp{ −E(h,v)}Z1exp{ −E(h,v)}⋅∂θ∂E(h,v)=−h,v∑P(h,v)⋅∂θ∂E(h,v)
所以,
∂ ∂ θ log P ( V ) = ∂ ∂ θ ① − ∂ ∂ θ ② = ∑ h , v P ( h , v ) ⋅ ∂ E ( h , v ) ∂ θ − ∑ h P ( h ∣ v ) ⋅ ∂ E ( h , v ) ∂ θ ⟺ ∂ ∂ w i j log P ( V ) = − ∑ h P ( h ∣ v ) ⋅ ∂ E ( h , v ) ∂ w i j + ∑ h , v P ( h , v ) ⋅ ∂ E ( h , v ) ∂ w i j \frac{\partial}{\partial\theta}\log P(V)=\frac{\partial}{\partial\theta}①-\frac{\partial}{\partial\theta}②\\=\sum_{h,v}P(h,v)\cdot\frac{\partial E(h,v)}{\partial\theta}-\sum_hP(h|v)\cdot\frac{\partial E(h,v)}{\partial\theta}\\\Longleftrightarrow\frac{\partial}{\partial w_{ij}}\log P(V)=-\sum_hP(h|v)\cdot\frac{\partial E(h,v)}{\partial w_{ij}}+\sum_{h,v}P(h,v)\cdot\frac{\partial E(h,v)}{\partial w_{ij}} ∂θ∂logP(V)=∂θ∂①−∂θ∂②=h,v∑P(h,v)⋅∂θ∂E(h,v)−h∑P(h∣v)⋅∂θ∂E(h,v)⟺∂wij∂logP(V)=−h∑P(h∣v)⋅∂wij∂E(h,v)+h,v∑P(h,v)⋅∂wij∂E(h,v)
因为:
E ( h , v ) = − ( h T W v + Δ ) = − ( ∑ i = 1 m ∑ j = 1 n h i w i j v j + Δ ) E(h,v)=-(h^TWv+\Delta)=-(\sum_{i=1}^m\sum_{j=1}^nh_iw_{ij}v_j+\Delta) E(h,v)=−(hTWv+Δ)=−(i=1∑mj=1∑nhiwijvj+Δ)
所以:
∂ ∂ w i j log P ( V ) = − ∑ h P ( h ∣ v ) ⋅ ( − h i v j ) + ∑ h , v P ( h , v ) ⋅ ( − h i v j ) = ∑ h P ( h ∣ v ) h i v j ⏟ ① − ∑ h , v P ( h , v ) h i v j ⏟ ② \frac{\partial}{\partial w_{ij}}\log P(V)=-\sum_hP(h|v)\cdot(-h_iv_j)+\sum_{h,v}P(h,v)\cdot(-h_iv_j)\\=\underset{①}{\underbrace{\sum_hP(h|v)h_iv_j}}-\underset{②}{\underbrace{\sum_{h,v}P(h,v)h_iv_j}} ∂wij∂logP(V)=−h∑P(h∣v)⋅(−hivj)+h,v∑P(h,v)⋅(−hivj)=① h∑P(h∣v)hivj−② h,v∑P(h,v)hivj
① = ∑ h 1 ∑ h 2 ⋯ ∑ h i ⋯ ∑ h m P ( h 1 , h 2 , ⋯ , h i , ⋯ , h m ∣ v ) ⋅ h i v j = ∑ h i P ( h i ∣ v ) ⋅ h i v j = P ( h i = 1 ∣ v ) ⋅ v j ①=\sum_{h_1}\sum_{h_2}\cdots\sum_{h_i}\cdots\sum_{h_m}P(h_1,h_2,\cdots,h_i,\cdots,h_m|v)\cdot h_iv_j\\=\sum_{h_i}P(h_i|v)\cdot h_iv_j\\=P(h_i=1|v)\cdot v_j ①=h1∑h2∑⋯hi∑⋯hm∑P(h1,h2,⋯,hi,⋯,hm∣v)⋅hivj=hi∑P(hi∣v)⋅hivj=P(hi=1∣v)⋅vj
② = ∑ h ∑ v P ( v ) ⋅ P ( h ∣ v ) ⋅ h i v j = ∑ v P ( v ) ∑ h P ( h ∣ v ) ⋅ h i v j = ∑ v P ( v ) ⋅ P ( h i = 1 ∣ v ) ⋅ v j ②=\sum_h\sum_vP(v)\cdot P(h|v)\cdot h_iv_j\\=\sum_v P(v)\sum_hP(h|v)\cdot h_iv_j\\=\sum_vP(v)\cdot P(h_i=1|v)\cdot v_j ②=h∑v∑P(v)⋅P(h∣v)⋅hivj=v∑P(v)h∑P(h∣v)⋅hivj=v∑P(v)⋅P(hi=1∣v)⋅vj
即,
∂ ∂ w i j log P ( V ) = P ( h i = 1 ∣ v ) ⋅ v j − ∑ v P ( v ) ⋅ P ( h i = 1 ∣ v ) ⋅ v j \frac{\partial}{\partial w_{ij}}\log P(V)=P(h_i=1|v)\cdot v_j-\sum_vP(v)\cdot P(h_i=1|v)\cdot v_j ∂wij∂logP(V)=P(hi=1∣v)⋅vj−v∑P(v)⋅P(hi=1∣v)⋅vj
∂ ∂ w i j 1 N ∑ V ∈ S log P ( V ) = 1 N ∑ V ∈ S ∂ ∂ w i j log P ( V ) \frac{\partial}{\partial w_{ij}}\frac1N\sum_{V\in S}\log P(V)=\frac1N\sum_{V\in S}\frac{\partial}{\partial w_{ij}}\log P(V) ∂wij∂N1V∈S∑logP(V)=N1V∈S∑∂wij∂logP(V)
For each v ∈ S : v\in S: v∈S:
\;\; v ( 0 ) ← v v^{(0)}\leftarrow v v(0)←v
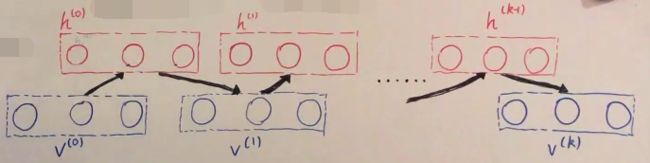
\;\; For l = 0 , 1 , 2 , ⋯ , k − 1 : l=0,1,2,\cdots,k-1: l=0,1,2,⋯,k−1: ( k s t e p s b l o c k G i b b s S a m p l i n g ) \color{red}{(k\;steps\;block\;Gibbs\;Sampling)} (kstepsblockGibbsSampling)
\;\; \;\; \;\; For i = 1 , 2 , ⋯ , m : i=1,2,\cdots,m: i=1,2,⋯,m:
\;\; \;\; \;\; \;\; \;\; sample h i ( l ) ∼ P ( h i ∣ v ( l ) ) h_i^{(l)}\sim P(h_i|v^{(l)}) hi(l)∼P(hi∣v(l))
\;\; \;\; \;\; For j = 1 , 2 , ⋯ , n : j=1,2,\cdots,n: j=1,2,⋯,n:
\;\; \;\; \;\; \;\; \;\; sample v j ( l + 1 ) ∼ P ( v j ∣ h ( l ) ) v_j^{(l+1)}\sim P(v_j|h^{(l)}) vj(l+1)∼P(vj∣h(l))
For i = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , n : i=1,2,\cdots,m,j=1,2,\cdots,n: i=1,2,⋯,m,j=1,2,⋯,n:
\;\; Δ w i j ← Δ w i j + ∂ ∂ w i j log P ( V ) \Delta w_{ij}\leftarrow\Delta w_{ij}+\frac{\partial}{\partial w_{ij}}\log P(V) Δwij←Δwij+∂wij∂logP(V)
\;\; ∂ ∂ w i j log P ( V ) ≈ P ( h i = 1 ∣ v ( 0 ) ) ⋅ v j ( 0 ) − P ( h i = 1 ∣ v ( k ) ) ⋅ v J ( k ) \frac{\partial}{\partial w_{ij}}\log P(V)\approx P(h_i=1|v^{(0)})\cdot v_j^{(0)}-P(h_i=1|v^{(k)})\cdot v_J^{(k)} ∂wij∂logP(V)≈P(hi=1∣v(0))⋅vj(0)−P(hi=1∣v(k))⋅vJ(k)
所以,
∂ ∂ w i j 1 N ∑ V ∈ S log P ( V ) = 1 N ∑ V ∈ S ∂ ∂ w i j log P ( V ) ≈ 1 N Δ w i j \frac{\partial}{\partial w_{ij}}\frac1N\sum_{V\in S}\log P(V)=\frac1N\sum_{V\in S}\frac{\partial}{\partial w_{ij}}\log P(V)\approx\frac1N\Delta w_{ij} ∂wij∂N1V∈S∑logP(V)=N1V∈S∑∂wij∂logP(V)≈N1Δwij
下一章传送门:白板推导系列笔记(二十五)-近似推断