决策树算法实战之预测眼镜类型
文章目录
- 一、说明
- 二、题目
-
- 2.1 概述
- 2.2 流程
- 三、实践
- 四、源代码
-
- 4.1 work01.ipynb
- 4.2 work01.py
- 5. 小结
一、说明
我是在jupyter完成的,然后导出成markdown格式,ipynb文件导出为markdown的命令如下:
jupyter nbconvert --to markdown xxx.ipynb
二、题目
2.1 概述
使用决策树预测患者需要佩戴的眼镜类型,根据数据集lenses.data,分为训练集和测试集,使用ID3算法,信息增益作为属性选择度量,自顶向下的分治方式构造决策树,从有类标号的训练元组中学习决策树,再用决策树对测试集分类,计算准确率和误分类率,评估分类器的性能。
2.2 流程
- 收集数据
lenses.txt文件 24行数据
young myope no reduced no lenses
young myope no normal soft
young myope yes reduced no lenses
young myope yes normal hard
young hyper no reduced no lenses
young hyper no normal soft
young hyper yes reduced no lenses
young hyper yes normal hard
pre myope no reduced no lenses
pre myope no normal soft
pre myope yes reduced no lenses
pre myope yes normal hard
pre hyper no reduced no lenses
pre hyper no normal soft
pre hyper yes reduced no lenses
pre hyper yes normal no lenses
presbyopic myope no reduced no lenses
presbyopic myope no normal no lenses
presbyopic myope yes reduced no lenses
presbyopic myope yes normal hard
presbyopic hyper no reduced no lenses
presbyopic hyper no normal soft
presbyopic hyper yes reduced no lenses
presbyopic hyper yes normal no lenses
- 准备数据:解析tab键分隔符的
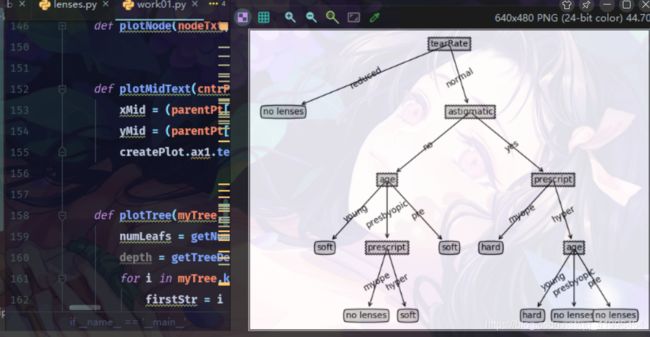
- 分析数据:快速检测数据,确保正确的解析数据内容,使用createPlot()函数绘制最终的树形图。
- 训练算法:使用createTree()函数
- 测试算法:编写测试函数验证决策树可以正确分类给定的数据实例
- 使用算法:存储数的数据结构,以便下次使用时无需重新构造树

三、实践
四、源代码
4.1 work01.ipynb
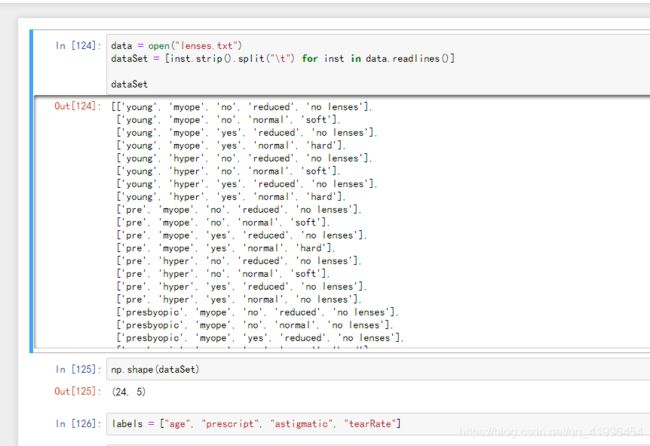
data = open("lenses.txt")
dataSet = [inst.strip().split("\t") for inst in data.readlines()]
dataSet
[['young', 'myope', 'no', 'reduced', 'no lenses'],
['young', 'myope', 'no', 'normal', 'soft'],
['young', 'myope', 'yes', 'reduced', 'no lenses'],
['young', 'myope', 'yes', 'normal', 'hard'],
['young', 'hyper', 'no', 'reduced', 'no lenses'],
['young', 'hyper', 'no', 'normal', 'soft'],
['young', 'hyper', 'yes', 'reduced', 'no lenses'],
['young', 'hyper', 'yes', 'normal', 'hard'],
['pre', 'myope', 'no', 'reduced', 'no lenses'],
['pre', 'myope', 'no', 'normal', 'soft'],
['pre', 'myope', 'yes', 'reduced', 'no lenses'],
['pre', 'myope', 'yes', 'normal', 'hard'],
['pre', 'hyper', 'no', 'reduced', 'no lenses'],
['pre', 'hyper', 'no', 'normal', 'soft'],
['pre', 'hyper', 'yes', 'reduced', 'no lenses'],
['pre', 'hyper', 'yes', 'normal', 'no lenses'],
['presbyopic', 'myope', 'no', 'reduced', 'no lenses'],
['presbyopic', 'myope', 'no', 'normal', 'no lenses'],
['presbyopic', 'myope', 'yes', 'reduced', 'no lenses'],
['presbyopic', 'myope', 'yes', 'normal', 'hard'],
['presbyopic', 'hyper', 'no', 'reduced', 'no lenses'],
['presbyopic', 'hyper', 'no', 'normal', 'soft'],
['presbyopic', 'hyper', 'yes', 'reduced', 'no lenses'],
['presbyopic', 'hyper', 'yes', 'normal', 'no lenses']]
np.shape(dataSet)
(24, 5)
labels = ["age", "prescript", "astigmatic", "tearRate"]
import numpy as np
from math import log
import operator as op
# 计算给定数据集的香农熵 熵越高数据越乱
def calcShannonEnt(dataSet):
'''
:param dataSet: 数据集
:return: 香农熵
'''
labelCounts = {
}
for featVec in dataSet:
currentLabel = featVec[-1]
if (currentLabel not in labelCounts.keys()):
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
rowNum = len(dataSet)
for key in labelCounts:
prob = float(labelCounts[key]) / rowNum
shannonEnt -= prob * log(prob, 2)
return shannonEnt
# 按照某个特征上的某个值来划分数据集 分成两份
def splitDataSet(dataSet, axis, value):
'''
:param dataSet: 数据集
:param axis: 特征index
:param value: 值
:return: 划分后的数据集
'''
retDataSet = []
for featVec in dataSet:
if (featVec[axis] == value):
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
# 划分数据集示例
splitDataSet(dataSet, 0,'young' )
[['myope', 'no', 'reduced', 'no lenses'],
['myope', 'no', 'normal', 'soft'],
['myope', 'yes', 'reduced', 'no lenses'],
['myope', 'yes', 'normal', 'hard'],
['hyper', 'no', 'reduced', 'no lenses'],
['hyper', 'no', 'normal', 'soft'],
['hyper', 'yes', 'reduced', 'no lenses'],
['hyper', 'yes', 'normal', 'hard']]
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
'''
:param dataSet: 数据集
:return: bestFeature
'''
# numFeatures=len(dataSet[0])-1 # 特征的数量(因每一行有一列类别,故减一)
numFeatures = np.shape(dataSet)[1] - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
'''
:param dataSet: 数据集
:return: bestFeature
'''
# numFeatures=len(dataSet[0])-1 # 特征的数量(因每一行有一列类别,故减一)
numFeatures = np.shape(dataSet)[1] - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
chooseBestFeatureToSplit(dataSet)
3
# 选取频率最高的类
def majorityCnt(classList):
'''
:param classList:
:return: 出现频率最高的类别名
'''
classCount = {
} # 存储class_list每个类标签出现的频率
for vote in classList:
if (vote not in classCount.keys()):
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=op.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
classList01 = [example[-1] for example in dataSet]
classList01
['no lenses',
'soft',
'no lenses',
'hard',
'no lenses',
'soft',
'no lenses',
'hard',
'no lenses',
'soft',
'no lenses',
'hard',
'no lenses',
'soft',
'no lenses',
'no lenses',
'no lenses',
'no lenses',
'no lenses',
'hard',
'no lenses',
'soft',
'no lenses',
'no lenses']
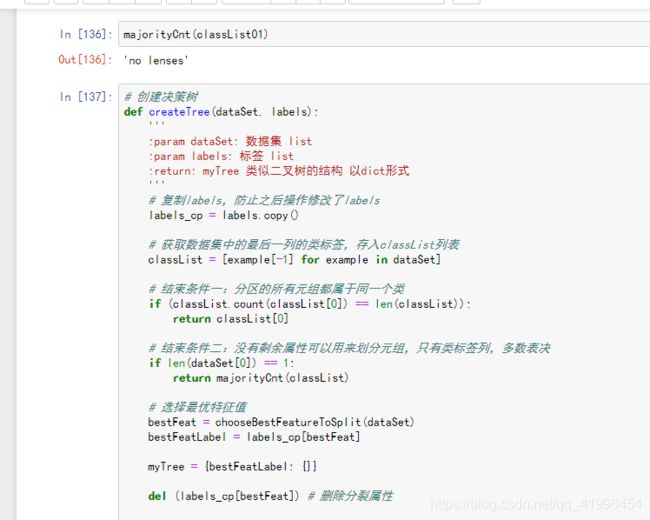
majorityCnt(classList01)
'no lenses'
# 创建决策树
def createTree(dataSet, labels):
'''
:param dataSet: 数据集 list
:param labels: 标签 list
:return: myTree 类似二叉树的结构 以dict形式
'''
# 复制labels,防止之后操作修改了labels
labels_cp = labels.copy()
# 获取数据集中的最后一列的类标签,存入classList列表
classList = [example[-1] for example in dataSet]
# 结束条件一:分区的所有元组都属于同一个类
if (classList.count(classList[0]) == len(classList)):
return classList[0]
# 结束条件二:没有剩余属性可以用来划分元组,只有类标签列,多数表决
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优特征值
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels_cp[bestFeat]
myTree = {
bestFeatLabel: {
}}
del (labels_cp[bestFeat]) # 删除分裂属性
# #将最好的属性所在列用集合取唯一值
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
# 递归
for value in uniqueVals:
subLabels = labels_cp[:]
# 对属性的每个取值作为分枝递归建立决策树
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
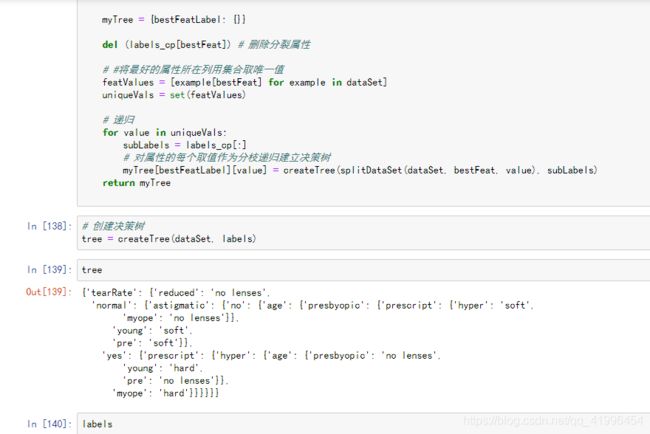
# 创建决策树
tree = createTree(dataSet, labels)
tree
{'tearRate': {'reduced': 'no lenses',
'normal': {'astigmatic': {'no': {'age': {'presbyopic': {'prescript': {'hyper': 'soft',
'myope': 'no lenses'}},
'young': 'soft',
'pre': 'soft'}},
'yes': {'prescript': {'hyper': {'age': {'presbyopic': 'no lenses',
'young': 'hard',
'pre': 'no lenses'}},
'myope': 'hard'}}}}}}
labels
['age', 'prescript', 'astigmatic', 'tearRate']
# 使用决策树分类
def classify(inputTree,featLabels,testVec):
'''
:param inputTree: list 决策树
:param featLabels: list 特征标签
:param testVec: list 测试样本的特征值
:return: classLabel 该样本所属的类别
'''
firstStr=list(inputTree.keys())[0]
# 源代码没有list,会产生错误:TypeError: 'dict_keys' object does not support indexing,
# 这是由于python3改变了dict.keys,返回的是dict_keys对象,支持iterable 但不支持indexable,我们可以将其明确的转化成list:
# print(firstStr)
# print(featLabels)
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
return classLabel
classify(tree, labels, ['young','myope','yes','normal'])
'hard'
分类器评估
准确率:
Accuracy=(TP+TN)/ALL = 0.8
错误率:
Error_rate=1-accuracy(M)=0.2
若对 no contact lenses类感兴趣
精度:
precision=正确分类的正元组/预测出的正元组=0.75
召回率:
Recall=TP/P=正确分类的正元组/实际正元组=1
# 画出决策树
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
# 获取节点数
def getNumLeafs(myTree):
numLeafs = 0
for i in myTree.keys():
firstStr = i
break
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
# 获取树的深度
def getTreeDepth(myTree):
maxDepth = 0
for i in myTree.keys():
firstStr = i
break
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt,
textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
for i in myTree.keys():
firstStr = i
break
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key], cntrPt, str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(inTree, (0.5, 1.0), '')
plt.show()
createPlot(tree)
# 评估模型
# 这里数据不够多,结果容易出现偏差
test_set=dataSet[18:24] # 取后6个作为测试集
train_set = dataSet[:18] # 取前18个作为训练集
print('训练集:\n', train_set)
训练集:
[['young', 'myope', 'no', 'reduced', 'no lenses'], ['young', 'myope', 'no', 'normal', 'soft'], ['young', 'myope', 'yes', 'reduced', 'no lenses'], ['young', 'myope', 'yes', 'normal', 'hard'], ['young', 'hyper', 'no', 'reduced', 'no lenses'], ['young', 'hyper', 'no', 'normal', 'soft'], ['young', 'hyper', 'yes', 'reduced', 'no lenses'], ['young', 'hyper', 'yes', 'normal', 'hard'], ['pre', 'myope', 'no', 'reduced', 'no lenses'], ['pre', 'myope', 'no', 'normal', 'soft'], ['pre', 'myope', 'yes', 'reduced', 'no lenses'], ['pre', 'myope', 'yes', 'normal', 'hard'], ['pre', 'hyper', 'no', 'reduced', 'no lenses'], ['pre', 'hyper', 'no', 'normal', 'soft'], ['pre', 'hyper', 'yes', 'reduced', 'no lenses'], ['pre', 'hyper', 'yes', 'normal', 'no lenses'], ['presbyopic', 'myope', 'no', 'reduced', 'no lenses'], ['presbyopic', 'myope', 'no', 'normal', 'no lenses']]
lenses_tree = createTree(test_set, labels)
print('决策树:\n', lenses_tree)
决策树:
{'tearRate': {'reduced': 'no lenses', 'normal': {'prescript': {'hyper': {'astigmatic': {'no': 'soft', 'yes': 'no lenses'}}, 'myope': 'hard'}}}}
# 测试分类
print('测试集:\n', test_set)
测试集:
[['presbyopic', 'myope', 'yes', 'reduced', 'no lenses'], ['presbyopic', 'myope', 'yes', 'normal', 'hard'], ['presbyopic', 'hyper', 'no', 'reduced', 'no lenses'], ['presbyopic', 'hyper', 'no', 'normal', 'soft'], ['presbyopic', 'hyper', 'yes', 'reduced', 'no lenses'], ['presbyopic', 'hyper', 'yes', 'normal', 'no lenses']]
# 测试分类器
def test_tree(D_set):
trueclass = 0
for row in range(5):
if classify(lenses_tree, labels,
[D_set[row][0], D_set[row][1], D_set[row][2], D_set[row][3]]) == D_set[row][4]:
trueclass += 1
print(D_set[row], classify(lenses_tree, labels,
[D_set[row][0], D_set[row][1], D_set[row][2], lenses[row][3]]))
correct_rate = trueclass / 5.0 # 分类的正确率
return correct_rate
score = test_tree(test_set)
print('正确率为:\n', score )
print('错误率为:\n', 1 - score)
['presbyopic', 'myope', 'yes', 'reduced', 'no lenses'] no lenses
['presbyopic', 'myope', 'yes', 'normal', 'hard'] hard
['presbyopic', 'hyper', 'no', 'reduced', 'no lenses'] no lenses
['presbyopic', 'hyper', 'no', 'normal', 'soft'] soft
['presbyopic', 'hyper', 'yes', 'reduced', 'no lenses'] no lenses
正确率为:
1.0
错误率为:
0.0
4.2 work01.py
import numpy as np
import operator as op
from math import log
# 计算给定数据集的香农熵 熵越高数据越乱
def calcShannonEnt(dataSet):
'''
:param dataSet: 数据集
:return: 香农熵
'''
labelCounts = {
}
for featVec in dataSet:
currentLabel = featVec[-1]
if (currentLabel not in labelCounts.keys()):
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
rowNum = len(dataSet)
for key in labelCounts:
prob = float(labelCounts[key]) / rowNum
shannonEnt -= prob * log(prob, 2)
return shannonEnt
# 按照某个特征上的某个值来划分数据集 分成两份
def splitDataSet(dataSet, axis, value):
'''
:param dataSet: 数据集
:param axis: 特征index
:param value: 值
:return: 划分后的数据集
'''
retDataSet = []
for featVec in dataSet:
if (featVec[axis] == value):
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
'''
:param dataSet: 数据集
:return: bestFeature
'''
# numFeatures=len(dataSet[0])-1 # 特征的数量(因每一行有一列类别,故减一)
numFeatures = np.shape(dataSet)[1] - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
# 选取频率最高的类
def majorityCnt(classList):
'''
:param classList:
:return: 出现频率最高的类别名
'''
classCount = {
}
for vote in classList:
if (vote not in classCount.keys()):
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=op.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
# 创建决策树
def createTree(dataSet, labels):
'''
:param dataSet: 数据集 list
:param labels: 标签 list
:return: myTree 类似二叉树的结构 以list形式
'''
classList = [example[-1] for example in dataSet]
if (classList.count(classList[0]) == len(classList)):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {
bestFeatLabel: {
}}
del (labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
# 使用决策树分类
def classify(inputTree, featLabels, testVec):
'''
:param inputTree: list 决策树
:param featLabels: list 特征标签
:param testVec: list 测试样本的特征值
:return:
'''
for i in inputTree.keys():
firstStr = i
break
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
if __name__ == '__main__':
data = open("lenses.txt")
dataSet = [inst.strip().split("\t") for inst in data.readlines()]
print(dataSet)
print(np.shape(dataSet))
labels = ["age", "prescript", "astigmatic", "tearRate"]
tree = createTree(dataSet, labels)
print(tree)
classify(tree, labels, ['young','myope','yes','normal'])
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
# 获取节点数
def getNumLeafs(myTree):
numLeafs = 0
for i in myTree.keys():
firstStr = i
break
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
# 获取树的深度
def getTreeDepth(myTree):
maxDepth = 0
for i in myTree.keys():
firstStr = i
break
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt,
textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
for i in myTree.keys():
firstStr = i
break
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key], cntrPt, str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(inTree, (0.5, 1.0), '')
plt.show()
createPlot(tree)
5. 小结
决策树分类器就像带有终止块的流程图,终止块表示分类结果。
开始处理数据集时,我们首先需要测量集合中数据的不一致性, 也就是熵,然后寻找最优方案划分数据集,直到数据集中的所有数据属于同- -分类。 ID3算法可以用于划分标称型数据集。构建决策树时,我们通常采用递归的方法将数据集转化为决策树。一般我们并不构造新的数据结构,而是使用Python语言内嵌的数据结构字典存储树节点信息。
使用Matplotlib的注解功能,我们可以将存储的树结构转化为容易理解的图形。
Python的pickle模块可用于存储决策树的结构。隐形眼镜的例子表明决策树可能会产生过多的数据集划分,从而产生过度匹配数据集的问题。我们可以通过裁剪决策树,合并相邻的无法产生大量信息增益的叶节点,消除过度匹配问题。