初识微积分二
微分和求导
- 导函数的定义:
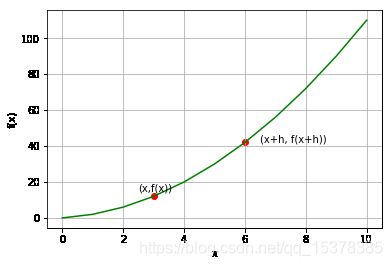
l i m h → 0 f ( x + h ) − f ( x ) h lim_{h \to 0} \frac{f(x + h) - f(x)}{h} limh→0hf(x+h)−f(x)
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)
f r a c d d x f ( x ) = lim h → 0 f ( x + h ) − f ( x ) h frac{d}{dx}f(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} fracddxf(x)=h→0limhf(x+h)−f(x)
%matplotlib inline
def f(x):
return x**2 + x
x = list(range(0, 11))
y = [f(i) for i in x]
x1 = 3
y1 = f(x1)
h = 3
x2 = x1+h
y2 = f(x2)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.plot(x,y, color='green')
plt.scatter(x1,y1, c='red')
plt.annotate('(x,f(x))',(x1,y1), xytext=(x1-0.5, y1+3))
plt.scatter(x2,y2, c='red')
plt.annotate('(x+h, f(x+h))',(x2,y2), xytext=(x2+0.5, y2))
plt.show()
导函数也可记为
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h ⇔ f ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a f'(\textbf{a}) = \lim_{h \to 0} \frac{f(\textbf{a} + h) - f(\textbf{a})}{h} \Leftrightarrow f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} f′(a)=h→0limhf(a+h)−f(a)⇔f′(a)=x→alimx−af(x)−f(a)
求导数
f ( x ) = x 2 + x f(x) = x^{2} + x f(x)=x2+x
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} f′(a)=h→0limhf(a+h)−f(a)
f ′ ( 2 ) = lim h → 0 f ( 2 + h ) − f ( 2 ) h f'(\textbf{2}) = \lim_{h \to 0} \frac{f(\textbf{2} + h) - f(\textbf{2})}{h} f′(2)=h→0limhf(2+h)−f(2)
f ′ ( 2 ) = lim h → 0 ( ( 2 + h ) 2 + 2 + h ) − ( 2 2 + 2 ) h f'(2) = \lim_{h \to 0} \frac{((2+h)^{2} + 2 + h) - (2^{2} + 2)}{h} f′(2)=h→0limh((2+h)2+2+h)−(22+2)
f ′ ( 2 ) = lim h → 0 ( h 2 + 5 h + 6 ) − 6 h = lim h → 0 h 2 + 5 h h = lim h → 0 h + 5 = 5 f'(2) = \lim_{h \to 0} \frac{(h^{2} + 5h + 6) - 6}{h} = \lim_{h \to 0} \frac{h^{2} + 5h}{h} = \lim_{h \to 0} h + 5 = 5 f′(2)=h→0limh(h2+5h+6)−6=h→0limhh2+5h=h→0limh+5=5
%matplotlib widget
def f(x):
return x**2 + x
x = list(range(0, 11))
y = [f(i) for i in x]
x1 = 2
y1 = f(x1)
m = 5
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.plot(x,y, color='green')
plt.scatter(x1,y1, c='red')
plt.annotate('(x,f(x))',(x1,y1), xytext=(x1-0.5, y1+3))
xMin = x1 - 5
yMin = y1 - (5*m)
xMax = x1 + 5
yMax = y1 + (5*m)
plt.plot([xMin,xMax],[yMin,yMax], color='magenta')
plt.show()
FigureCanvasNbAgg()
求导函数
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)
f ′ ( x ) = lim h → 0 ( ( x + h ) 2 + x + h ) − ( x 2 + x ) h f'(x) = \lim_{h \to 0} \frac{((x+h)^{2} + x + h) - (x^{2} + x)}{h} f′(x)=h→0limh((x+h)2+x+h)−(x2+x)
f ′ ( x ) = lim h → 0 x 2 + h 2 + 2 x h + x + h − x 2 − x h f'(x) = \lim_{h \to 0} \frac{x^{2} + h^{2} + 2xh + x + h - x^{2} - x}{h} f′(x)=h→0limhx2+h2+2xh+x+h−x2−x
f ′ ( x ) = lim h → 0 h 2 + 2 x h + h h f'(x) = \lim_{h \to 0} \frac{h^{2} + 2xh + h}{h} f′(x)=h→0limhh2+2xh+h
f ′ ( x ) = lim h → 0 2 x + h + 1 f'(x) = \lim_{h \to 0} 2x + h + 1 f′(x)=h→0lim2x+h+1
f ′ ( x ) = 2 x + 1 f'(x) = 2x + 1 f′(x)=2x+1
可微
并不是所有的函数都是可以求导函数的。
可微的函数有下面的几何特征
- 连续
- 切线不竖直
- 光滑
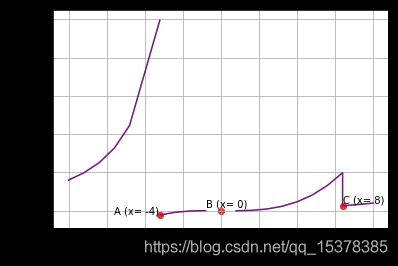
q ( x ) = { 40 , 000 x 2 , if x < − 4 , ( x 2 − 2 ) ⋅ ( x − 1 ) , if x ≠ 0 and x ≥ − 4 and x < 8 , ( x 2 − 2 ) , if x ≠ 0 and x ≥ 8 q(x) = \begin{cases} \frac{40,000}{x^{2}}, & \text{if } x < -4, \\ (x^{2} -2) \cdot (x - 1), & \text{if } x \ne 0 \text{ and } x \ge -4 \text{ and } x < 8, \\ (x^{2} -2), & \text{if } x \ne 0 \text{ and } x \ge 8 \end{cases} q(x)=⎩⎪⎨⎪⎧x240,000,(x2−2)⋅(x−1),(x2−2),if x<−4,if x=0 and x≥−4 and x<8,if x=0 and x≥8
%matplotlib inline
def q(x):
if x != 0:
if x < -4:
return 40000 / (x**2)
elif x < 8:
return (x**2 - 2) * x - 1
else:
return (x**2 - 2)
x = [*range(-10, -5), -4.01]
x2 = [*range(-4, 8), 7.9999, *range(8, 11)]
y = [q(i) for i in x]
y2 = [q(i) for i in x2]
plt.xlabel('x')
plt.ylabel('q(x)')
plt.grid()
plt.plot(x,y, color='purple')
plt.plot(x2,y2, color='purple')
plt.scatter(-4,q(-4), c='red')
plt.annotate('A (x= -4)',(-5,q(-3.9)), xytext=(-7, q(-3.9)))
plt.scatter(0,0, c='red')
plt.annotate('B (x= 0)',(0,0), xytext=(-1, 40))
plt.scatter(8,q(8), c='red')
plt.annotate('C (x= 8)',(8,q(8)), xytext=(8, 100))
plt.show()
- A不连续
- B不连续
- C不光滑
求导规则
基本规则
f ( x ) = π ∴ f ′ ( x ) = 0 f(x) = \pi \;\; \therefore \;\; f'(x) = 0 f(x)=π∴f′(x)=0
f ( x ) = 2 g ( x ) ∴ f ′ ( x ) = 2 g ′ ( x ) f(x) = 2g(x) \;\; \therefore \;\; f'(x) = 2g'(x) f(x)=2g(x)∴f′(x)=2g′(x)
f ( x ) = g ( x ) + h ( x ) ∴ f ′ ( x ) = g ′ ( x ) + h ′ ( x ) f(x) = g(x) + h(x) \;\; \therefore \;\; f'(x) = g'(x) + h'(x) f(x)=g(x)+h(x)∴f′(x)=g′(x)+h′(x)
f ( x ) = k ( x ) − l ( x ) ∴ f ′ ( x ) = k ′ ( x ) − l ′ ( x ) f(x) = k(x) - l(x) \;\; \therefore \;\; f'(x) = k'(x) - l'(x) f(x)=k(x)−l(x)∴f′(x)=k′(x)−l′(x)
d d x ( 2 x + 6 ) = d d x 2 x + d d x 6 = 2 \frac{d}{dx}(2x + 6) = \frac{d}{dx} 2x + \frac{d}{dx} 6 = 2 dxd(2x+6)=dxd2x+dxd6=2
幂规则
极其常用的规则
\begin{equation}f(x) = x^{n} ;; \therefore ;; f’(x) = nx^{n-1}\end{equation}
例如:
f ( x ) = x 3 ∴ f ′ ( x ) = 3 x 2 f(x) = x^{3} \;\; \therefore \;\; f'(x) = 3x^{2} f(x)=x3∴f′(x)=3x2
f ( x ) = x − 2 ∴ f ′ ( x ) = − 2 x − 3 f(x) = x^{-2} \;\; \therefore \;\; f'(x) = -2x^{-3} f(x)=x−2∴f′(x)=−2x−3
f ( x ) = x 2 ∴ f ′ ( x ) = 2 x f(x) = x^{2} \;\; \therefore \;\; f'(x) = 2x f(x)=x2∴f′(x)=2x
幂规则的推导
f ( x ) = x 2 f(x) = x^{2} f(x)=x2
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)
f ′ ( x ) = lim h → 0 ( x + h ) 2 − x 2 h f'(x) = \lim_{h \to 0} \frac{(x + h)^{2} - x^{2}}{h} f′(x)=h→0limh(x+h)2−x2
f ′ ( x ) = lim h → 0 x 2 + h 2 + 2 x h − x 2 h = lim h → 0 h 2 + 2 x h h = lim h → 0 h + 2 x = 2 x f'(x) = \lim_{h \to 0} \frac{x^{2} + h^{2} + 2xh - x^{2}}{h} = \lim_{h \to 0} \frac{h^{2} + 2xh}{h} = \lim_{h \to 0} h + 2x = 2x f′(x)=h→0limhx2+h2+2xh−x2=h→0limhh2+2xh=h→0limh+2x=2x
乘法规则
d d x [ f ( x ) g ( x ) ] = f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) \frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x) dxd[f(x)g(x)]=f′(x)g(x)+f(x)g′(x)
例如
f ( x ) = 2 x 2 f(x) = 2x^{2} f(x)=2x2
g ( x ) = x + 1 g(x) = x + 1 g(x)=x+1
f ′ ( x ) = 4 x f'(x) = 4x f′(x)=4x
g ′ ( x ) = 1 g'(x) = 1 g′(x)=1
d d x [ f ( x ) g ( x ) ] = ( 4 x ⋅ ( x + 1 ) ) + ( 2 x 2 ⋅ 1 ) \frac{d}{dx}[f(x)g(x)] = (4x \cdot (x + 1)) + (2x^{2} \cdot 1) dxd[f(x)g(x)]=(4x⋅(x+1))+(2x2⋅1)
d d x [ f ( x ) g ( x ) ] = 6 x 2 + 4 x \frac{d}{dx}[f(x)g(x)] = 6x^{2} + 4x dxd[f(x)g(x)]=6x2+4x
商数规则
r ( x ) = s ( x ) t ( x ) r(x) = \frac{s(x)}{t(x)} r(x)=t(x)s(x)
r ′ ( x ) = s ′ ( x ) t ( x ) − s ( x ) t ′ ( x ) ( t ( x ) ) 2 r'(x) = \frac{s'(x)t(x) - s(x)t'(x)}{(t(x))^{2}} r′(x)=(t(x))2s′(x)t(x)−s(x)t′(x)
例如
s ( x ) = 3 x 2 s(x) = 3x^{2} s(x)=3x2
t ( x ) = 2 x t(x) = 2x t(x)=2x
r ′ ( x ) = ( 6 x ⋅ 2 x ) − ( 3 x 2 ⋅ 2 ) ( 2 x ) 2 = 6 x 2 4 x 2 = 3 2 r'(x) = \frac{(6x \cdot 2x) - (3x^{2} \cdot 2)}{(2x)^{2}} = \frac{6x^{2}}{4x^{2}} = \frac{3}{2} r′(x)=(2x)2(6x⋅2x)−(3x2⋅2)=4x26x2=23
链式规则
d d x [ o ( i ( x ) ) ] = o ′ ( i ( x ) ) ⋅ i ′ ( x ) \frac{d}{dx}[o(i(x))] = o'(i(x)) \cdot i'(x) dxd[o(i(x))]=o′(i(x))⋅i′(x)
例如
i ( x ) = x 2 i(x) = x^{2} i(x)=x2
o ( x ) = 2 x o(x) = 2x o(x)=2x
o ′ ( x ) = 2 , i ′ ( x ) = 2 x o'(x) = 2, i'(x) = 2x o′(x)=2,i′(x)=2x
d d x [ o ( i ( x ) ) ] = 4 x \frac{d}{dx}[o(i(x))] = 4x dxd[o(i(x))]=4x
极值和优化
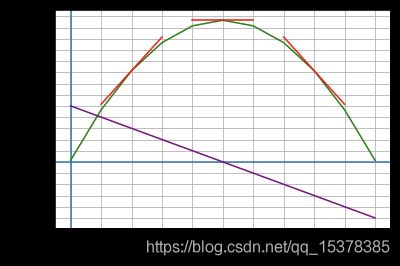
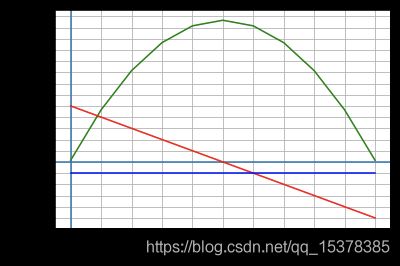
对函数 k ( x ) = − 10 x 2 + 100 x + 3 {k(x) = -10x^{2} + 100x + 3} k(x)=−10x2+100x+3 有导函数:
k ′ ( x ) = − 20 x + 100 k'(x) = -20x + 100 k′(x)=−20x+100
%matplotlib inline
def k(x):
return -10*(x**2) + (100*x) + 3
def kd(x):
return -20*x + 100
x = list(range(0, 11))
y = [k(i) for i in x]
yd = [kd(i) for i in x]
plt.axhline()
plt.axvline()
plt.xlabel('x (time in seconds)')
plt.ylabel('k(x) (height in feet)')
plt.xticks(range(0,15, 1))
plt.yticks(range(-200, 500, 20))
plt.grid()
plt.plot(x,y, color='green')
plt.plot(x,yd, color='purple')
x1 = 2
x2 = 5
x3 = 8
plt.plot([x1-1,x1+1],[k(x1)-(kd(x1)),k(x1)+(kd(x1))], color='r')
plt.plot([x2-1,x2+1],[k(x2)-(kd(x2)),k(x2)+(kd(x2))], color='r')
plt.plot([x3-1,x3+1],[k(x3)-(kd(x3)),k(x3)+(kd(x3))], color='r')
plt.show()
找最大值和最小值
对 k ( x ) = − 10 x 2 + 100 x + 3 {k(x) = -10x^{2} + 100x + 3} k(x)=−10x2+100x+3 有 k ′ ( x ) = − 20 x + 100 {k'(x) = -20x + 100 } k′(x)=−20x+100
− 20 x + 100 = 0 -20x + 100 = 0 −20x+100=0
x = 5 x = 5 x=5
如果求二阶导数
k ′ ( x ) = − 20 x + 100 ⇒ k ′ ′ ( x ) = − 20 k'(x) = -20x + 100 \Rightarrow k''(x) = -20 k′(x)=−20x+100⇒k′′(x)=−20
根据二阶导数为常量,而且是负常量,得知一阶导函数是线性下降的。导函数为0的点就是极大值。
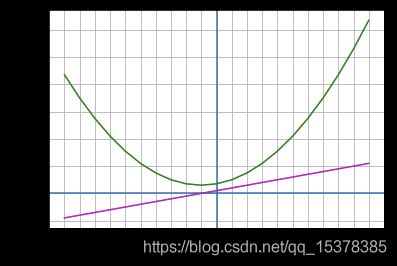
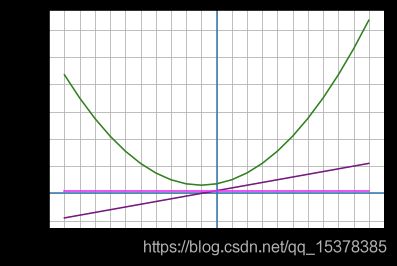
函数
w ( x ) = x 2 + 2 x + 7 w(x) = x^{2} + 2x + 7 w(x)=x2+2x+7
%matplotlib inline
def w(x):
return (x**2) + (2*x) + 7
def wd(x):
return 2*x + 2
x = list(range(-10, 11))
y = [w(i) for i in x]
yd = [wd(i) for i in x]
plt.axhline()
plt.axvline()
plt.xlabel('x')
plt.ylabel('w(x)')
plt.xticks(range(-10,15, 1))
plt.yticks(range(-200, 500, 20))
plt.grid()
plt.plot(x,y, color='g')
plt.plot(x,yd, color='m')
plt.show()
极值点
对函数
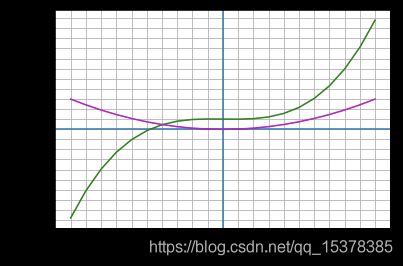
v ( x ) = x 3 − 2 x + 100 v(x) = x^{3} - 2x + 100 v(x)=x3−2x+100
%matplotlib widget
def v(x):
return (x**3) - (2*x) + 100
def vd(x):
return 3*(x**2) - 2
x = list(range(-10, 11))
y = [v(i) for i in x]
yd = [vd(i) for i in x]
plt.axhline()
plt.axvline()
plt.xlabel('x')
plt.ylabel('v(x)')
plt.xticks(range(-10,15, 1))
plt.yticks(range(-1000, 2000, 100))
plt.grid()
plt.plot(x,y, color='g')
plt.plot(x,yd, color='m')
plt.show()
FigureCanvasNbAgg()
%matplotlib inline
def k(x):
return -10*(x**2) + (100*x) + 3
def kd(x):
return -20*x + 100
def k2d(x):
return -20
plt.axhline()
plt.axvline()
x = list(range(0, 11))
y = [k(i) for i in x]
yd = [kd(i) for i in x]
y2d = [k2d(i) for i in x]
plt.xlabel('x')
plt.ylabel('k(x)')
plt.xticks(range(0,15, 1))
plt.yticks(range(-200, 500, 20))
plt.grid()
plt.plot(x,y, color='g')
plt.plot(x,yd, color='r')
plt.plot(x,y2d, color='b')
plt.show()
练习:
w ( x ) = x 2 + 2 x + 7 w(x) = x^{2} + 2x + 7 w(x)=x2+2x+7
%matplotlib inline
def w(x):
return (x**2) + (2*x) + 7
def wd(x):
return 2*x + 2
def w2d(x):
return 2
x = list(range(-10, 11))
y = [w(i) for i in x]
yd = [wd(i) for i in x]
y2d = [w2d(i) for i in x]
plt.axhline()
plt.axvline()
plt.xlabel('x (time in days)')
plt.ylabel('w(x) (flowers)')
plt.xticks(range(-10,15, 1))
plt.yticks(range(-200, 500, 20))
plt.grid()
plt.plot(x,y, color='green')
plt.plot(x,yd, color='purple')
plt.plot(x,y2d, color='magenta')
plt.show()
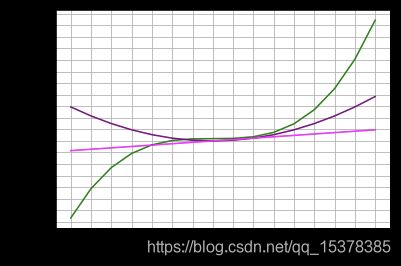
极值点不一定是最大值或者最小值
v ( x ) = x 3 − 6 x 2 + 12 x + 2 v(x) = x^{3} - 6x^{2} + 12x + 2 v(x)=x3−6x2+12x+2
v ′ ( x ) = 3 x 2 − 12 x + 12 = 0 v'(x) = 3x^{2} - 12x + 12 = 0 v′(x)=3x2−12x+12=0
x = 2 {x = 2} x=2 是极值点
%matplotlib inline
def v(x):
return (x**3) - (6*(x**2)) + (12*x) + 2
def vd(x):
return (3*(x**2)) - (12*x) + 12
def v2d(x):
return (3*(2*x)) - 12
from matplotlib import pyplot as plt
x = list(range(-5, 11))
y = [v(i) for i in x]
yd = [vd(i) for i in x]
y2d = [v2d(i) for i in x]
plt.xlabel('x')
plt.ylabel('v(x)')
plt.xticks(range(-10,15, 1))
plt.yticks(range(-2000, 2000, 50))
plt.grid()
plt.plot(x,y, color='green')
plt.plot(x,yd, color='purple')
plt.plot(x,y2d, color='magenta')
plt.show()
print ("v(2) = " + str(v(2)))
print ("v'(2) = " + str(vd(2)))
print ("v''(2) = " + str(v2d(2)))
v(2) = 10
v'(2) = 0
v''(2) = 0