非‘玩具’的隐式多尺度深度均衡模型

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

尽管绝大多数深度网络都是基于一个核心的概念---神经“层”的叠加，我们提出一种只有一层、但是却可以代表无限层叠加的隐性深度模型（implicit-depth model)：深度平衡模型（DEQ）。基于这一设计，我们进一步提出了多尺度的深度平衡模型（multiscale DEQ，或MDEQ），并讨论MDEQ是如何同步驱动多个特征流来达到并行的特征平衡点（synchronized feature equilibria）。

白绍杰：本科毕业于美国卡内基梅隆大学（CMU）计算机系和应用数学系（双学士），目前是CMU机器学习系四年级博士生，导师为J.Zico Kolter教授。研究方向主要集中在深度时间序列模型，以及融合数学优化模型和深度学习结构，并从而构建稳定、低内存、易于分析的隐性深度学习（implicit deep learning）方法。

一、相关背景

在计算机视觉和音频处理等领域，最先进的模式识别系统几乎普遍基于多层层次特征提取器。这些模型是分阶段构建的：输入通过一系列连续的块进行处理，每个块以不同的分辨率操作。这个体系结构明确地表达了层次结构，用上采样层和下采样层在不同规模的连续块之间转换。这种设计的一个重要动机是在这些领域中突出的多尺度结构和极高的信号维数。例如，一个典型的图像包含数百万个像素，这些像素必须由模型进行一致的处理。

诸如神经ODE（NODEs）和深均衡模型（DEQ）等隐式深层网络的最新进展例证了可微分建模的替代方法。这些结构用模型必须满足的解析条件替换显式的、深度叠放的层，并且能够在恒定的内存占用范围内模拟具有“无限”深度的模型。隐式建模的一个显著成就是其成功应用于自然语言处理中的大规模序列。

但隐式深度学习与一般模式识别任务相关吗？其中一个明显的挑战是隐性网络去掉了灵活的“层次”和“阶段”。因此，尚不清楚他们是否可以适当地对多尺度结构进行建模，而多尺度结构在某些领域中对高分辨能力是至关重要的。这是激发我们工作的挑战，放弃层次和阶段的深层序列的隐式模型（implicit models），能否在具有丰富多尺度结构特征的领域（如计算机视觉）获得具有竞争力的精度?

为了应对这一挑战，本文引入了一类新的隐式网络：多尺度深度均衡模型（MDEQ）。它受到 DEQs的启发，DEQs在序列建模中获得了很高的准确性。我们充分扩展了DEQ的构造，以引入多种信号分辨率的同时均衡建模。MDEQ通过在所有特征尺度上直接优化稳定表示，同时解决了多个分辨率流的平衡。与标准的显式深层网络不同，MDEQ不会连续处理不同的分辨率，而较高的分辨率会流入较低的分辨率，反之亦然。相反，不同的特征尺度在一个单一的“浅”模型中被并行处理，并驱动到平衡点。

这种设计带来两个主要优点。首先，像基本的DEQ一样，我们的模型不需要通过显式层堆栈进行反向传播，并且在训练过程中具有O(1)内存占用量。这一点特别重要，因为模式识别系统会占用大量内存。其次，MDEQ修正了DEQ的一个缺点，在平衡状态下暴露了多个特征尺度，从而为辅助损失和复合训练程序提供自然的接口，如预训练(例如，在ImageNet上)和微调(例如，在分割或检测任务上)。多尺度建模使单个MDEQ能够同时训练在不同尺度上定义的多个损失，其平衡特征可以作为各种任务的“头”。

我们通过对大规模图像分类和语义分割数据集进行广泛的实验来证明MDEQ的有效性。值得注意的是，这种浅层隐式模型的准确度水平可与最新的深层显式模型相提并论。在ImageNet分类中，MDEQ在参数计数相似情况下优于基准ResNet（例如ResNet-101），达到了77.5%的top-1精度。在Cityscapes语义分割上，用于ImageNet实验的MDEQs与最近的显式模型的性能相当，同时消耗的内存也少得多。我们最大的MDEQ在Cityscapes验证集上超过了80%mIoU，胜过强大的卷积网络，并且非常接近最优效果。到目前为止，这是迄今为止隐式深度学习的最大规模应用，对于直到最近才主要应用于“玩具”领域的一类模型而言，这是一个了不起的结果。

1.1  隐式深度学习

几乎所有现代深度学习方法都使用显式模型，该模型提供用于正向传播的显式计算图。反向传播在同一图形中按相反顺序进行。这种方法是深度学习流行的框架的核心，并且与“架构”的概念相关联。相反，隐式模型没有规定的计算图。他们假定模型必须满足一个特定的标准(例如，ODE流的端点，或方程的根)。重要的是，驱动模型满足这一标准的算法并没有规定。因此，隐式模型可以在其前向传播中利用黑匣子解算器，并享受独立于前向传递轨迹的后向解析传播。

隐状态的隐式建模已经被深度学习社区探索了几十年。Pineda和Almeida研究了训练递归动态的隐式微分技术，也被称为递归反向传播(RBP)。网络设计的隐式方法最近引起了新的兴趣。例如，Neural ODE (NODEs)使用隐式ODE求解器对递归残差块进行建模，相当于采用无穷小步骤的连续ResNet。深度均衡模型（DEQ）使用黑盒寻根方法求解序列模型的不动点，等效于找到无限层网络的极限状态。隐式建模的其他实例包括优化层，可微物理引擎，逻辑结构学习和连续生成模型。

我们的工作将深度均衡方法引入以丰富的多尺度结构特征的信号域中。我们开发了第一个单层隐式深度模型，该模型能够缩放到现实的视觉任务（例如，百万像素级图像），并在这些情况下获得竞争性结果。相比之下，由于数值的不稳定性，基于ODE的模型到目前为止仅应用于相对低维的信号。例如，Chen等将28×28 MNIST图像降采样为7×7，然后再将其提供给神经ODE。更广泛地讲，我们的工作可以看作是隐式模型的新视角，其中模型定义和优化多个数据流的同时标准，这些数据流可以有不同的维度。到目前为止，虽然DEQs和NODEs是在单个特征流上定义的，但是单个MDEQ可以针对不同的任务联合优化特征，比如图像分割和分类。

1.2  计算机视觉中的多尺度建模

计算机视觉是层次多尺度建模的典型应用领域。深度卷积网络已成为该领域的主导。计算机视觉问题可以从所需输出粒度的角度来看待：从低分辨率（如整个图像的标签）到高分辨率输出（如语义分割中为每个像素分配标签）。这些问题的最先进模型被明确构造为以不同分辨率运行的处理的连续阶段。例如，一个ResNet通常包括4-6个连续的阶段，每一个操作的分辨率是前一个的一半。DenseNet使用不同的连接模式在层之间传递信息，但共享总体结构：一系列阶段。其他设计会逐渐降低特征分辨率，然后逐步提高它。还可以按照明确编排的顺序重复进行下采样和上采样。

多尺度建模一直是计算机视觉的中心主题。拉普拉斯金字塔是多尺度建模的一个有影响的早期例子。Farabet等人将多尺度处理与卷积网络相结合进行场景解析。并且已经在许多随后的架构中明确地解决了。

我们的工作为隐式深度网络带来了多尺度建模。MDEQ本质上只有一个阶段，其中不同的分辨率并存。输入以最高分辨率注入，然后隐式传播到其他标度，这些标度由（黑匣子）求解器同时进行优化，以驱动它们满足联合平衡条件。就像DEQs一样，MDEQ能够代表“无限”的深度网络，而只需要恒定的内存成本。

二、多尺度深度均衡模型

我们首先简要概述基本的DEQ构造以及将其扩展到计算机视觉时出现的一些主要挑战。

2.1  深层平衡(DEQ):通用公式

DEQ方法的核心思想之一是权重绑定：同一组参数可以在深度网络的各个层之间共享。形式化描述在隐含状态z上用参数θ制定了一个L层权重变换，公式如下：(1)

输入x会输入到每一层中。当确保足够的稳定性条件时，无限堆叠这些层（即L→∞）显示出基本上执行定点迭代，因此趋于达到平衡z^*=f_θ(z^*;x)。直观地，当我们迭代变换f_θ 时，隐藏表示趋于收敛到稳定状态z*。这种结构具有许多吸引人的特性。首先，我们可以直接求解不动点，这比显式遍历各层要快得多。我们将此公式化为寻根问题：

例如，人们可以利用牛顿或准牛顿方法来实现二次或超线性收敛到根。其次，可以使用g_θ的雅可比行列式在z*处直接向后传播平衡状态，而无需追溯正向寻根过程。形式上，给定损耗ℓ= L(z*,y)（其中y是目标），可以将梯度用隐函数定理（implicit function theorem）表示为：

这意味着DEQ的前向遍历可以依赖于任何黑盒根求解器，而后向遍历则是基于平衡时仅通过一层（或块）的区分而独立建立的。内存消耗只有一个块而不是L→∞块。由于g_θ的雅可比行列式计算起来可能很昂贵，因此DEQs可以求解涉及向量-雅可比乘积的线性方程，这要便宜的多：

挑战：我们刚刚总结的，主要是针对序列的处理。当我们从序列过渡到高分辨率图像时，我们注意到这些领域之间的重要差异。

首先，不同于典型的自回归序列学习问题(如语言建模)，其中的输入和输出具有相同的长度和维度，一般模式识别系统(如视觉系统)需要通过结构中的上采样和下采样的组合进行多阶段建模。基本的DEQ构造没有这种结构。 

其次，诸如图像分类（标签）或对象定位（区域）之类的计算机视觉任务的输出可能与输入（完整图像）具有非常不同的尺寸：这也是基本DEQ不支持的功能。

第三，用于任务（例如语义分割）的最新模型通常基于“主干”，这些主干已针对图像分类进行了预训练，任务在结构上有所不同并且其输出也有不同尺寸。目前还不清楚DEQ结构如何支持这种转移。

第四，尽管DEQs过去的序列建模工作中可以利用一些最近提出的先进参数共享（weight-tied）体系结构来进行序列建模，作为设计fθ变换的基础，但在最先进的计算机视觉建模中还不存在这样最先进模型对等物。

 

2.2  MDEQ模型

MDEQ架构图如下所示：

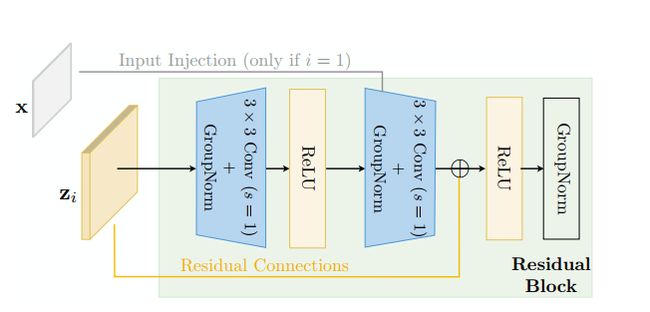
图 1  尺度深度平衡模型(MDEQ)的结构

图1中显示了模型的所有组件。MDEQ由一个被驱动到平衡态的变换f_θ组成。不同尺度的特征同时并存，并被同时驱动到平衡状态。

MDEQ的中心部分是驱动转换为平衡的变换f_θ。我们使用一个简单的设计，首先通过残差块获取每个分辨率下的特征，块很浅并且结构相同。在分辨率i下，残差块接收内部状态Z_i，并以相同的分辨率输出变换后的特征张量。

图2  MDEQ中使用的residual block

 

剩余块的内部结构如图2所示。出于稳定性的原因，我们在很大程度上采用He et al.等人的设计，但使用组归一化而非批处理归一化。分辨率为i的残差块可以正式表示为：

在这些块之后，f_θ的第二部分是一个多分辨率融合步骤，混合不同尺度的特征地图(见图1)。变换后的特征从当前尺度i到其他尺度进行上采样或下采样。在我们的构造中，下采样是通过j-i连续2步3×3 Conv2d进行的，而上采样是通过直接双线性插值进行的。标尺j的最终输出是通过对所有传入标尺i提供的变换后的特征图求和而形成的；即每个比例尺的输出特征张量是所有比例尺的变换特征的混合。这迫使所有比例尺上的特征保持一致，并使整个系统达到协调平衡，从而协调各个比例尺上的表示。

输入表示：原始输入首先经过变换（例如，对齐要素通道的线性层）以形成x，并将其提供给f_θ。这种输入注入的存在对于隐式模型至关重要，因为它（连同θ）将动力学系统的流量与输入相关联。但是，与某些显式视觉体系结构使用的多尺度输入表示法不同，我们仅将x注入到最高分辨率的特征流中。输入以单个（完整）分辨率提供给MDEQ。因此，较低的分辨率始于根本不了解输入的状态。当（黑匣子）求解器将所有尺度逐渐驱动至平衡不动点z*时，这些信息将在此过程中被“隐式”地传播到各个特征尺度下。

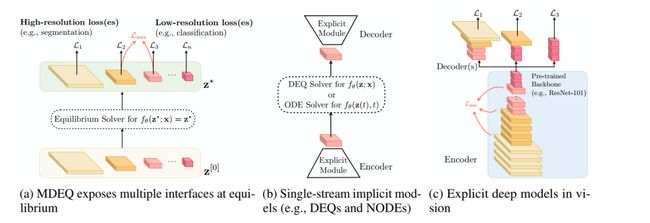
图3  MDEQ与先前的隐式模型和标准的显式模型

在计算机视觉中的视觉比较

多预训练和辅助损失：图3比较了MDEQ与单流隐式模型（例如DEQ）和计算机视觉中的显式深层网络。这些不同模型揭示了不同的“界面”，可用于定义不同任务的损失。先前的隐式模型（例如神经ODEs和DEQs）通常假定损失是在隐式隐藏状态的单个流上定义的，其具有统一的输入和输出形状。因此，目前尚不清楚如何在结构上不同的任务之间灵活地转移此类模型（例如，先进行图像分类人物的预训练，以及再在语义分割人物上进行微调）。此外，没有自然的方法来定义辅助损耗，因为作为一个没有“层”的结构，正向和反向传播的计算轨迹是解耦的。

相比之下，MDEQ以多种分辨率向其状态公开了方便的“接口”。一种分辨率（最高）可以与输入的分辨率相同，并且可以用于定义密集预测任务（例如语义分割）的损失。另一种分辨率（最低）可以是空间尺寸被折叠的矢量，并且可以用于定义图像级标记任务（例如图像分类）的损失。这建议使用清晰的协议来针对不同任务训练同一模型，或者联合，或者按顺序。

三、实验

3.1 与CIFAR-10上已有的隐式模型比较

我们在CIFAR-10分类上进行了50个epochs的实验，并比较了参数数量大致相同的模型。但是，与基于ODE的方法不同，我们不会在将输入传递到MDEQ解算器之前,对原始图像执行下采样。训练MDEQ模型时，所有分辨率都用于最终预测：更高分辨率的流会经过附加的下采样层，并添加到最低分辨率的输出中以进行预测。

表1  CIFAR-10结果

 

表1中显示了CIFAR-10图像分类的MDEQ模型的结果。与NODE和增强型NODE相比，具有相似参数计数的小型MDEQ可以将精度提高20个百分点以上：将错误减少的幅度超过了两倍。MDEQ还改进了单流DEQ。最终，更大的MDEQ可以匹配甚至超过具有相同容量的ResNet-18的精度：这是隐式模型首次证明了这种性能。

3.2  ImageNet分类

我们测试MDEQ扩展到更高分辨率图像的更大数据集的能力：ImageNet。与CIFAR-10分类一样，我们在MDEQ模块之后增加了一个浅分类层，以融合不同尺度的均衡输出，并对综合损失进行训练。我们对小型MDEQ模型和大型MDEQ进行了基准测试，以提供与许多参考模型(如ResNet-18、-34、-50和-101)进行适当比较。注意，MDEQ只有一层residual blocks，然后是多分辨率融合。因此，为了匹配标准显式模型的容量，我们需要增加MDEQ内的特征维数。这主要是通过在残差块内调整卷积滤波器的宽度来实现的(见图2)。

表2  ImageNet分类top-1和top-5的准确率

表2显示了两种不同尺寸的MDEQs在计算机视觉中相对于知名参考模型的精度。MDEQs与强大的显式模型比非常有竞争力。例如，一个带有18M参数的小型MDEQ性能优于ResNet-18 (13M参数)、ResNet-34 (21M参数)，甚至优于ResNet-50 (26M参数)。较大的MDEQ (64M参数)达到与ResNet-101 (52M参数)相同的性能水平。这远远超出了隐式建模之前应用的规模和精度水平。

3.3 Cityscapes高分辨率街景图片的语义分割

在ImageNet上训练后，我们将同一MDEQ继续在在Cityscapes数据集上进行语义分割任务的微调。注意在此过程中我们使用的是和图像分类任务里的同一个MDEQ模型，但是相比起ImageNet里使用其最低分辨率的特征流的设定，在语义分割中我们使用最高分辨率的平衡点来定义损失函数。具体结果如下：

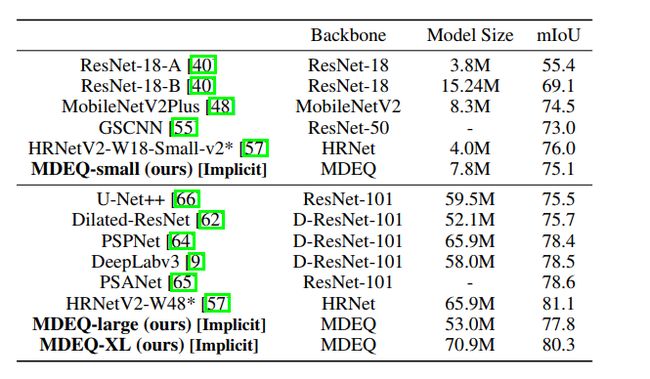
表3  城市景观数据集效果

MDEQ达到很高的准确性。它们接近当前的最新水平，并且匹配或优于过去两年发布的众所周知且经过精心设计的显式模型。较小的MDEQ（780万个参数）的平均IoU为75.1。这在相同大小的MobileNetV2Plus上进行了改进，并且对于这种规模的模型而言，它接近SOTA。较大的MDEQ（53.5M参数）达到77.8 mIoU，在备受赞誉的最新语义分段模型（如DeepLabv3和PSPNet）相差不到1个百分点之内，而较大版本的MDEQ（70.9M参数）则超过了它们。令人惊讶的是，尽管基于以前未应用到该领域的原理，我们的结果说明了可以通过“浅层”隐式模型实现这种级别的准确性。

 

3.4 运行时长和内存消耗

我们提供了使用CIFAR-10数据的MDEQs运行时间和内存分析，输入批处理大小为32。由于先前的隐式模型相对较小，我们提供了MDEQ和MDEQ-small的结果，以便进行公平的比较。所有的计算速度都是基于单个RTX 2080 Ti GPU上，所有计算速度均相对于ResNet-101模型（每批约150ms）进行基准测试。结果如下图所示：

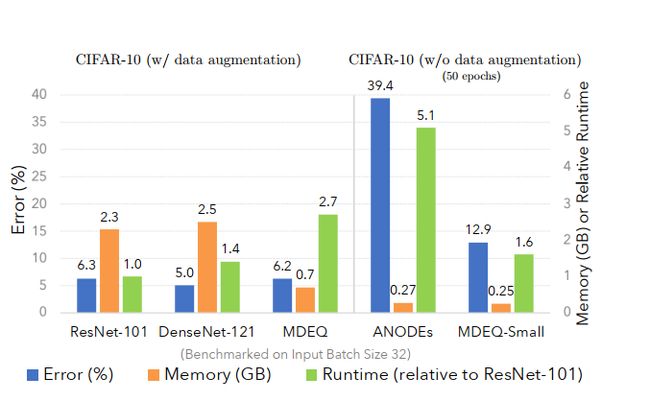
图4  CIFAR-10上的运行时间和内存消耗

与显式模型（例如ResNets和DenseNets）相比，MDEQ在训练时节省了60％以上的GPU内存，同时保持了竞争优势。在ImageNet上训练大型MDEQ会消耗大约6GB的内存，而这大部分是Broyden求根法存储中间状态的消耗。这种低内存占用是反向传播的直接结果。同时，MDEQs通常比显式网络慢。

与ResNet-101相比，我们发现MDEQ的速度降低了2.7倍，这种趋势类似于在序列域中观察到的趋势。导致这种放缓的一个主要因素是，MDEQs始终在所有分辨率下保持特性，而诸如ResNets的显式模型会逐渐降低激活样本，从而减少计算量。但是，与具有172K参数的 ANODEs相比，类似大小的MDEQ速度快了3倍，而错误减少了3倍。

 

 四、总结

本文介绍了多尺度深度均衡模型（MDEQs）：一种新的用于高维和多尺度结构领域的隐式体系结构。与先前的隐式模型（例如DEQ和Neural ODEs）不同，MDEQ通过以不同分辨率对多个特征表示进行同步平衡来求解和反向传播。我们证明了单个MDEQ可以用于不同的任务，例如图像分类和语义分割。我们的实验首次证明“浅层”隐式模型适用于实际的计算机视觉任务，并获得与显式架构相匹配的竞争性能，这些显式架构的特征是通过深度堆叠的层进行顺序处理。

隐式模型在这项工作中的出色表现提出了机器学习中的核心问题。迄今为止在深度学习中占主导地位的复杂的阶段式分层架构是否必要？MDEQ举例说明了一种不同的建模方法。这种方法在实践中可能比以前出现的方法更具实用性。这将有助于隐式深度学习的发展，并将进一步扩大可微分建模的议程。

  e           m     t

往期精彩

 AI                i

整理：李健铨

审稿：白绍杰

排版：岳白雪

AI TIME欢迎AI领域学者投稿，期待大家剖析学科历史发展和前沿技术。针对热门话题，我们将邀请专家一起论道。同时，我们也长期招募优质的撰稿人，顶级的平台需要顶级的你！

请将简历等信息发至[email protected]！

微信联系:AITIME_HY

AI TIME是清华大学计算机系一群关注人工智能发展，并有思想情怀的青年学者们创办的圈子,旨在发扬科学思辨精神，邀请各界人士对人工智能理论、算法、场景、应用的本质问题进行探索，加强思想碰撞，打造一个知识分享的聚集地。

更多资讯请扫码关注

 

（直播回放：https://b23.tv/2HhvCD）

（点击“阅读原文”下载本次报告ppt）