关于Prim算法和Kruskal算法

      Prim算法和Kruskal算法都是描述连通图的最小生成树(最小权重生成树),也就是极小连通子图.( 就是在连接原图所有节点的情况下,使边的权值相加最小的通路)

Prim算法

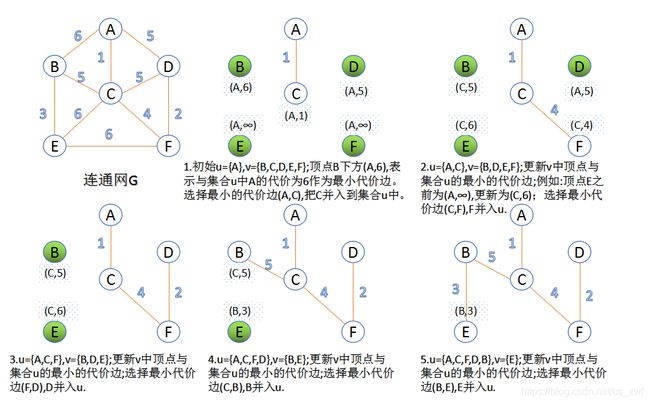
      Prim算法的思路是随机从图上一个节点出发,选择与该节点连接的边中权值最小的边,再从该节点和与之相连的另一节点出发选择权值最小的边,但是新选择的节点和边不能与原有节点,边构成圈,以此类推,直至连接所有节点.

    如下图,在选择了A,C,F,D后有三条权值为5的边,为什么选择BC而不选择其他的呢?因为如果选择AD,ACFD构成圈,选择CD,则CDF构成圈, 因为是最小生成树,所以除树根外,树的各节点都只有一个父亲节点,树是不会构成类似圈的形状( 术语忘了,就是描述的样子)

 算法代码构成思路:

     图的结构我使用的是邻接表

    1.使用一个全局数组visited[] , 如果最小权值边确认下来, 边两边的节点都被访问过了,以节点为横坐标的visited数组 等于 1,在寻找新的权值最小边的时候,边的另一节点不能在visited数组上,即visited数组不能为1.

    2.寻找新的权值最小边时, 出发节点要从visited数组为1的节点处,遍历与他们相连的所有边,寻找权值最小的边.( 当然我这种做法可能会使在寻找第二处等以后的边时,前面的最小权值边被重复遍历,又因visited数组为1而遍历后面)

Kruskal算法

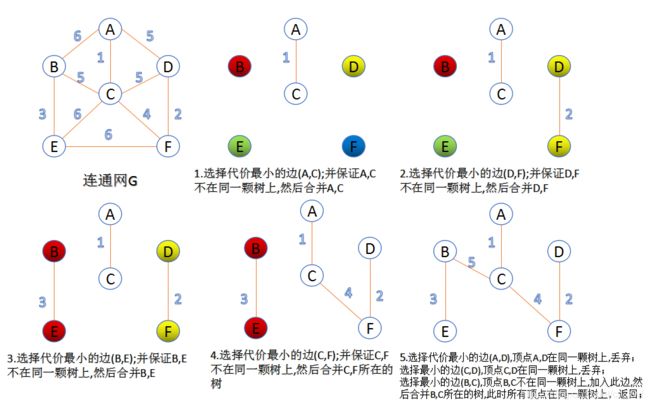
   Kruskal算法的思路是在图中寻找权值最小的边,然后排除该边后,在剩余边中寻找权值最小的边,,但是新选择的节点和边不能与原有节点,边构成圈以此类推直至连接所有节点. 

   要避免的情况其实和Prim算法差不多

算法代码构成思路:

     1.遍历邻接表,将所有边的节点,权值输入到一个结构体数组中,数组根据权值升序排序

     2.一个source函数, fat数组  以节点为横坐标的fat数组的值为它本身( 横坐标值 ).

     3.如果刚来时 头两个节点相连,那么其中一个节点的fat数组的值为另一节点.一个节点的源头为另一节点

     4. 后面的俩个节点,其中一个节点的源头的节点的fat数组的值为另一节点源头

Kruskal算法可以参考https://blog.csdn.net/qq_41754350/article/details/81460643

 

两个算法的证明

简单证明prim算法

反证法：如果prim生成的不是最小生成树

1).设prim生成的树为G0

2).如果存在Gmin使得cost(Gmin)不属于G0

3).将增加G0中可得一个环。且不是该环的最长边(这是由于∈Gmin)

4).这与prim每次生成最短边矛盾

5).故如果不成立，命题得证.

简单证明Kruskal算法

对图的顶点数n做归纳，证明Kruskal算法对随意n阶图适用。

归纳基础：

n=1。显然能够找到最小生成树。

归纳过程：

如果Kruskal算法对n≤k阶图适用，那么，在k+1阶图G中。我们把最短边的两个端点a和b做一个合并操作，即把u与v合为一个点v'。把原来接在u和v的边都接到v'上去。这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边)，G'最小生成树T'能够用Kruskal算法得到。

我们证明T'+{}是G的最小生成树。

用反证法，如果T'+{}不是最小生成树，最小生成树是T。即W(T)})。

显然T应该包括，否则，能够用增加到T中，形成一个环，删除环上原有的随意一条边，形成一棵更小权值的生成树。而T-{}。是G'的生成树。所以W(T-{})<=W(T')。也就是W(T)<=W(T')+W()=W(T'+{})，产生了矛盾。于是如果不成立。T'+{}是G的最小生成树。Kruskal算法对k+1阶图也适用。

由数学归纳法，Kruskal算法得证。

证明引用自https://www.cnblogs.com/zhchoutai/p/8687614.html

算法过程图图片引用自https://blog.csdn.net/a2392008643/article/details/81781766

 

如有错误或者不当,请多担当

我的代码:https://github.com/zhangweifeng66/algorithms/blob/master/Kruska