最优化问题(二) 之 拉格朗日乘子法和KKT

1. 基本概念

前面我们有提到，拉格朗日乘子法和KKT求解约束优化问题的思路就是：
将有约束的问题转化为无约束的问题 (最优化问题(一))。转换的主要思想是将约束条件函数与原函数联立，从而求出使原函数取得极值的各个变量的解。

等式约束时使用拉格朗日乘子法，不等约束时使用KKT条件。

2. 数学定义

考虑约束优化问题：

2.1 等式约束

对于等式约束问题，

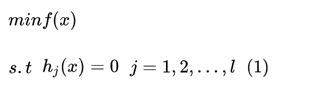
拉格朗日乘子法的做法是对原目标函数进行改造，一般包含如下几个步骤：
1）构造拉格朗日函数
2）解变量的偏导方程
3）带入目标函数

拉格朗日乘子法构造的新目标函数如下：

$F(x,\delta )=f(x)+{\sum }_{j=1}^l{\delta }_j{h}_j(x)$

其中，$f(x)$是原始目标函数，$h_j(x)$为第$j$个不等式约束，${\delta }_j$为对应的约束系数。相当于是将目标函数和约束项加权求和。

然后，分别对每一个变量求导，注意：此时权重 $\delta$ 也是自变量。相当于：
$\frac{\partial F}{\partial x_i}=0$，……

$\frac{\partial F}{\partial {\delta }_j}=0$，……

下面我们结合例子理解一下。给定椭圆:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

求这个椭球内接长方体的最大体积。

这个问题实际上就是条件极值问题，即在条件$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ 下，求 $f(x,y,z)=8xyz$ 的最大值。

1）带入拉格朗日乘子法中，新目标函数为：
$$\begin{array}{rl}F(x,y,z)& =f(x,y,z)+\delta h(x,y,z)\\ & =8xyz+\delta (\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1)\end{array}$$

2）对 $F(x,y,z,\delta )$ 求偏导可得：

$$\frac{\partial F(x,y,z,\delta )}{\partial x}=8yz+\frac{2\delta x}{a^2}=0$$
$$\frac{\partial F(x,y,z,\delta )}{\partial y}=8xz+\frac{2\delta y}{b^2}=0$$
$$\frac{\partial F(x,y,z,\delta )}{\partial z}=8xy+\frac{2\delta z}{c^2}=0$$
$$\frac{\partial F(x,y,z,\delta )}{\partial \delta }=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1=0$$
解方程可得：
$x=\frac{\sqrt{3}}{3}a$，$y=\frac{\sqrt{3}}{3}b$，$x=\frac{\sqrt{3}}{3}c$

3）带入原始目标函数，求得：

$V_{max}=f(\frac{\sqrt{3}}{3}a,\frac{\sqrt{3}}{3}b,\frac{\sqrt{3}}{3}c)=\frac{8\sqrt{3}}{9}abc$

至此，通过拉格朗日乘子法求得了该等式约束下的最大值。

那么为什么可以这么转换呢？

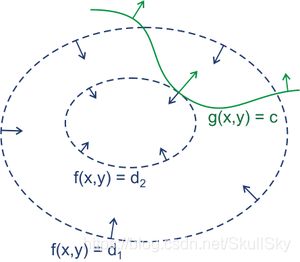
借用维基百科上的例子，对于如下二维优化问题：

$minf(x,y)$, S.t. $g(x,y)=c$

目标函数 $f(x,y)$ 的等高线如下图蓝色线，箭头代表斜率。约束 $g(x,y)$ 如下图绿色线所示，也就是说最优解一定是落在绿色线上的。不难看出，当等高线与绿色的线相切时，即为最优解。而相切时，$f(x,y)$ 和 $g(x,y)$ 在切点的梯度是在一条直线上的。因此有：

$\nabla f(x,y)=\lambda (\nabla g(x,y)-c)$

其中，$\lambda$为非零的实数。

但实际实现过程中，直接求偏导为0这一方法使用的较少，一般都是采用优化算法迭代拟合，如梯度下降。具体原因可以参见求最优值，梯度下降算法 or 偏导等于0 ?。

2.2 不等式约束

对于不等式约束问题，

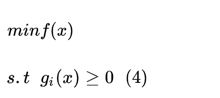
如果直接套用拉格朗日乘子法，会得到如下表达式：

$F(x,\delta )=f(x)+{\sum }_{i=1}^m{\beta }_i{g}_i(x)$

其中，$f(x)$是原始目标函数，$g_i(x)$为第$i$个不等式约束，${\beta }_i$为对应的约束系数。我们引入了KKT条件，

KKT条件是说最优值必须满足以下条件：

1）L(a, b, x)对x求导为零；

2）h(x) =0;

3）a*g(x) = 0;
　　　　
这一块我也没怎么看懂☺️，后续看懂后再补齐。