回溯算法

一、什么是回溯算法

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

回溯算法实际上一个类似枚举的深度优先搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回（也就是递归返回），尝试别的路径。

二、回溯算法思想

  回溯法一般都用在要给出多个可以实现最终条件的解的最终形式。回溯法要求对解要添加一些约束条件。总的来说，如果要解决一个回溯法的问题，通常要确定三个元素：

1、选择。对于每个特定的解，肯定是由一步步构建而来的，而每一步怎么构建，肯定都是有限个选择，要怎么选择，这个要知道；同时，在编程时候要定下，优先或合法的每一步选择的顺序，一般是通过多个if或者for循环来排列。

2、条件。对于每个特定的解的某一步，他必然要符合某个解要求符合的条件，如果不符合条件，就要回溯，其实回溯也就是递归调用的返回。

3、结束。当到达一个特定结束条件时候，就认为这个一步步构建的解是符合要求的解了。把解存下来或者打印出来。对于这一步来说，有时候也可以另外写一个issolution函数来进行判断。注意，当到达第三步后，有时候还需要构建一个数据结构，把符合要求的解存起来，便于当得到所有解后，把解空间输出来。这个数据结构必须是全局的，作为参数之一传递给递归函数。

三、递归函数的参数的选择，要遵循四个原则

1、必须要有一个临时变量(可以就直接传递一个字面量或者常量进去)传递不完整的解，因为每一步选择后，暂时还没构成完整的解，这个时候这个选择的不完整解，也要想办法传递给递归函数。也就是，把每次递归的不同情况传递给递归调用的函数。

2、可以有一个全局变量，用来存储完整的每个解，一般是个集合容器（也不一定要有这样一个变量，因为每次符合结束条件，不完整解就是完整解了，直接打印即可）。

3、最重要的一点，一定要在参数设计中，可以得到结束条件。一个选择是可以传递一个量n，也许是数组的长度，也许是数量，等等。

4、要保证递归函数返回后，状态可以恢复到递归前，以此达到真正回溯。

四、例题

N皇后

难度：困难
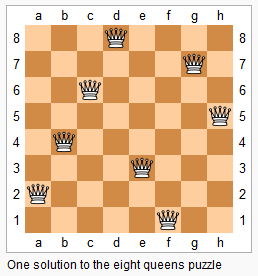
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],

["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
解释: 4 皇后问题存在两个不同的解法。
提示：
皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。
当然，她横、竖、斜都可走一到七步，可进可退。（引用自 百度百科 - 皇后 ）
来源： 添加链接描述
代码思路：
这道题是经典的回溯题，开始我们先要考虑一下怎么生成棋盘并且将“皇后”放入其中，我们可以用二维数组来建立起一个棋盘mark，之后将数组中的每个元素设置成为0来代表是空位，之后用1来代表放置的皇后和皇后所能吃子的范围（就是不能再放入新皇后的位置）之后我们用方向数组的方法来将棋盘上不能放皇后的位置改成1，这样棋盘的函数就写好了。
接下来我们再建立一个和棋盘mark类似的数组location来保存皇后的位置，建立方式和棋盘一样，只不过是用字符串的形式，在没有皇后的位置用‘.'来表示，用’Q‘来表示皇后的位置。
最后开始建立递归函数，因为每一行最多只能有一个皇后，那么我们就每次递归一行棋盘来考虑，每一行只要mark位置上是0就可以放皇后，之后每次递归到下一行，在递归之前用一个临时棋盘来保存现在的棋盘用来之后的回溯用，当我们递归到某行的时候发现没有皇后的位置可以放置了，那么我就要回溯了，返回到没有放皇后的时候，之后换成另一个位置来放置皇后的位置，经过这样的递归一直到n行都放置了皇后就可以结束递归了。

#include
#include
#include
#include
#include
using namespace std;
class Solution {
public:
    vector >solveNQueens(int n)
    {
        vector >result;
        vector >mark;
        vectorlocation;
        for (int i = 0;i < n;++i)
        {
            mark.push_back((vector()));
            for (int j = 0;j < n;++j)
            {
                mark[i].push_back(0);
            }
            location.push_back("");
            location[i].append(n, '.');
        }
        generate(0, n, location, result, mark);
        return result;
    }
private:
    void put_down_the_queen(int x, int y,//棋盘函数
        vector >& mark)
    {
        static const int dx[] = { -1,1,0,0,-1,-1,1,1 };
        static const int dy[] = { 0,0,-1,1,-1,1,-1,1 };
        mark[x][y] = 1;
        for (int i = 1;i < mark.size();++i)
        {
            for (int j = 0;j < 8;++j)
            {
                int new_x = x + i * dx[j];
                int new_y = y + i * dy[j];
                if (new_x >= 0 && new_x < mark.size()
                    && new_y >= 0 && new_y < mark.size())
                    mark[new_x][new_y] = 1;
            }
        }
    }
    void generate(int k, int n, vector& location,//递归函数
        vector >& result, vector >& mark)
    {
        if (k == n)
        {
            result.push_back(location);
            return;
        }
        for (int i = 0;i < n;++i)
        {
            if (mark[k][i] == 0)
            {
                vector >tmp_mark = mark;
                location[k][i] = 'Q';
                put_down_the_queen(k, i, mark);
                generate(k + 1, n, location, result, mark);
                mark = tmp_mark;
                location[k][i] = '.';
            }
        }
    }
};

int main()
{
     //测试案例
    vector >result;
    Solution solve;
    result = solve.solveNQueens(4);
    for (int i = 0;i < result.size();++i)
    {
        cout << "i = " << i<

 

 例二：

78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
分析思路：

给定一个集合比如｛1，2，3｝，求该集合的所有子集。
对于集合中的每一个元素，在某一子集中只有两种状态，要么在子集中，要么不在子集中。

因此对于一个含有n个元素的集合来说，对其中的某一个元素i，用xi来表示其在某一子集中的状态，xi=1表示在子集中，xi=0表示不在子集中，因此，解可以表示为：
｛x1,x2,x3,x4……xn｝;一共有2^n个向量。那么可以写代码如下.

#include
#include
#include
#include
#include
#include
using namespace std;
void function(int i, vector& num, vector& item, vector >& result)
{
    if (i == num.size()) return;
        item.push_back(num[i]);
        result.push_back(item);
        function(i+1, num, item, result);
        item.pop_back();
        function(i + 1, num, item, result);
}
int main()
{ 
    vectornum;
    num.push_back(1);
    num.push_back(2);
    num.push_back(3);
    vectoritem;
    vector >result;
    function(0, num, item, result);
    for (int i = 0;i < result.size();++i)
    {
        for (int j = 0;j < result[i].size();++j)
        {
            cout << "[" << result[i][j] << "]";
        }
        cout << endl;
    }
}

 

另外一种解题方法(位运算)：
对于集合{A,B,C}来说，可将每元素转还成二进制的100、010、001三个数，之后对于只有三个元素的集合来说，他的子集个数是2^3个，转化成二进制就是000、001、010、011、100、101、110、111八个数，之后对于每个元素是否出行只要用&运算出是否为真便可。

#include
#include
#include
#include
#include
#include
using namespace std;
vector > function(vector& v)
{
    vector > result;
    int all = 1 << v.size();
    for (int i = 0;i < all;++i)
    {
        vector item;
        for (int j = 0;j < v.size();++j)
        {
            if (i & (1 << j)) item.push_back(v[j]);
        }
        result.push_back(item); 
    }
    return result;
}
int main()
{ 
    vectornum;
    num.push_back(1);
    num.push_back(2);
    num.push_back(3);
    vectoritem;
    vector >result=function(num);
    for (int i = 0;i < result.size();++i)
    {
        for (int j = 0;j < result[i].size();++j)
        {
            cout << "[" << result[i][j] << "]";
        }
        cout << endl;
    }
}