机器学习笔记二:使用LogisticRegression实现鸢尾花逻辑回归分类
一、LogisticRegression 类
sklearn.linear_model.LogisticRegression (penalty='l2', *,
dual=False,
tol=0.0001, C=1.0,
fit_intercept=True,
intercept_scaling=1,
class_weight=None,
random_state=None,
solver='lbfgs',
max_iter=100,
multi_class='auto',
verbose=0,
warm_start=False,
n_jobs=None,
l1_ratio=None)
各个参数的含义,可以参考以下这篇文章:
LogisticRegression - 参数说明
二、案例
1、导入相关模块
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
2、加载数据集
# 载入数据集,Y的值有0,1,2三种情况,每种特征150个样本
iris = load_iris()
X = iris.data[:, :2] #获取花卉两列数据集
Y = iris.target
print(np.shape(X))
print(np.shape(Y))
(150, 2)
(150,)
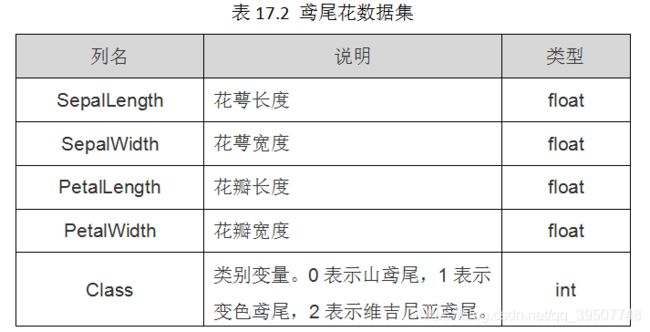
该数据集一共包含4个特征变量,1个类别变量。共有150个样本,iris是鸢尾植物,这里存储了其萼片和花瓣的长宽,共4个属性,鸢尾植物分三类:
上面为了简单,我们只选取了前两个特征来做逻辑回归。
3、对数据做一些格式转换
X=pd.DataFrame(X)
Y=pd.DataFrame(Y)
X.columns=["Sepal length","Sepal width"]
Y.columns=["class"]
print(X.head())
print(Y.head())
Y=Y.loc[:,"class"]
Sepal length Sepal width
0 5.1 3.5
1 4.9 3.0
2 4.7 3.2
3 4.6 3.1
4 5.0 3.6
class
0 0
1 0
2 0
3 0
4 0
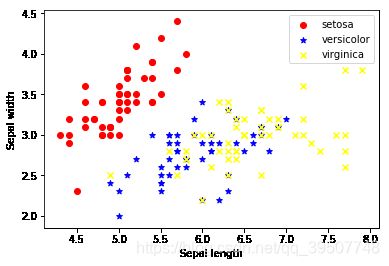
4、画出散点图,先看一下数据分布情况
setosa=plt.scatter(X.loc[:,"Sepal length"][Y==0],
X.loc[:,"Sepal width"][Y==0],
color='red', marker='o', label='setosa')
versicolor=plt.scatter(X.loc[:,"Sepal length"][Y==1],
X.loc[:,"Sepal width"][Y==1],
color='blue', marker='*', label='versicolor')
virginica=plt.scatter(X.loc[:,"Sepal length"][Y==2],
X.loc[:,"Sepal width"][Y==2],
color='yellow', marker='x', label='virginica')
plt.legend((setosa,versicolor,virginica),
('setosa','versicolor','virginica'))
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.show()
lr = LogisticRegression(C=1e5)
lr = lr.fit(X,Y)
6、预测、计算分类准确度
y_pred= lr.predict(X)
print(accuracy_score(Y,y_pred))
0.8066666666666666
#打印出预测结果,以及逻辑回归得到的三条分界线的斜率和截距
print(y_pred)
print(lr.coef_)
print(lr.intercept_)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 1 2 1 2 1 2 1 1 1 1 1 1 2 1 1 1 1 2 1 1 1
2 2 2 2 1 1 1 1 1 1 1 2 2 1 1 1 1 2 1 1 1 1 1 2 1 1 2 1 2 2 2 2 1 2 2 2 2
2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 2 1 2
2 1]
[[-30.61879527 27.54963779]
[ 0.14041199 -3.21392459]
[ 2.60373147 -0.74348327]]
[ 77.73711825 8.02399007 -14.19811218]
7、可视化分类结果
#由函数关系在散点图上绘制出三条边界线,直观的看一下分类效果
#c+a*x1+b*x2=0
fig=plt.figure()
a1=lr.coef_[0][0]
b1=lr.coef_[0][1]
c1=lr.intercept_[0]
a2=lr.coef_[1][0]
b2=lr.coef_[1][1]
c2=lr.intercept_[1]
a3=lr.coef_[2][0]
b3=lr.coef_[2][1]
c3=lr.intercept_[2]
x=X.loc[:,"Sepal length"]
y1=-(c1+a1*x)/b1
y2=-(c2+a2*x)/b2
y3=-(c3+a3*x)/b3
plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
setosa=plt.scatter(X.loc[:,"Sepal length"][Y==0],
X.loc[:,"Sepal width"][Y==0],
color='red', marker='o', label='setosa')
versicolor=plt.scatter(X.loc[:,"Sepal length"][Y==1],
X.loc[:,"Sepal width"][Y==1],
color='blue', marker='*', label='versicolor')
virginica=plt.scatter(X.loc[:,"Sepal length"][Y==2],
X.loc[:,"Sepal width"][Y==2],
color='yellow', marker='x', label='virginica')
plt.legend((setosa,versicolor,virginica),
('setosa','versicolor','virginica'))
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.xlim((4, 8))
plt.ylim((2, 4.5))
plt.show()
可以看到,图中三条直线是要将数据分成三类,但是分类效果并不是很好,准确度只有0.8。这是因为这里我们只是做一下演示,重点在于实现逻辑回归的步骤,并没有去优化算法。
比如,你可以选择使用全部四个特征去分类,或者自己增加一些这些自变量(特征)的多次项等等。需要注意的是,和线性回归使用均方误差不同,逻辑回归在进行梯度下降的时候使用的是交叉熵损失函数。