机器学习之数据预处理——缺失值填充

机器学习之数据预处理——缺失值

上一节给大家回顾了Pandas进行数据预处理会用到哪些方法，学习缺失值简单的填充方法（0、unknown、均值等），这节课学习线性回归法填补缺失值和拉格朗日插值法。

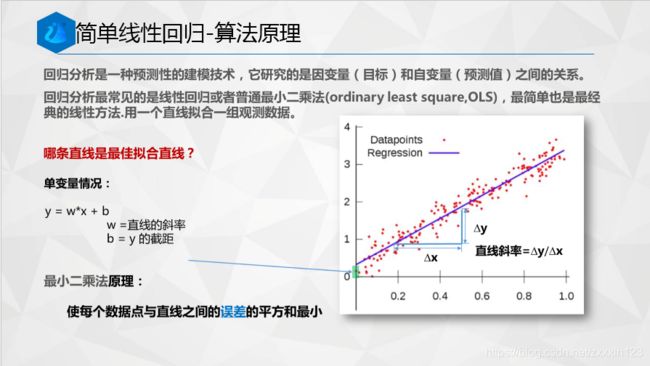
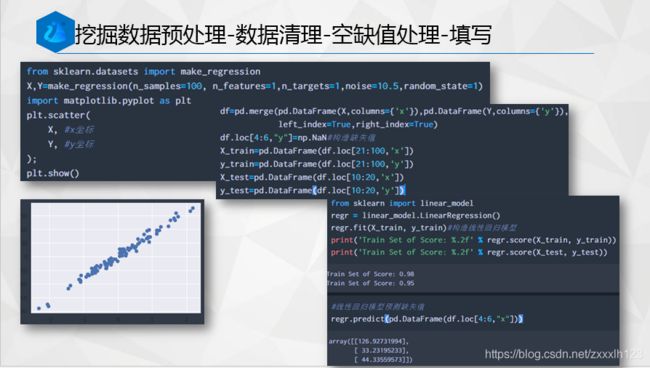
1.线性回归法填补缺失值

#随机生成一个线性回归数据
from sklearn.datasets import make_regression
X,Y=make_regression(n_samples=100, n_features=1,n_targets=1,noise=10.5,random_state=1)
import matplotlib.pyplot as plt
plt.scatter(
    X, #x坐标
    Y, #y坐标
);
plt.show()

x=np.arange(100)
y=3*x+4
data={
     'x':x,'y':y}
df=pd.DataFrame(data)
df.loc[4:6,"y"]=np.NaN#构造缺失值
X_train=pd.DataFrame(df.loc[21:100,'x'])
y_train=pd.DataFrame(df.loc[21:100,'y'])
X_test=pd.DataFrame(df.loc[10:20,'x'])
y_test=pd.DataFrame(df.loc[10:20,'y'])

from sklearn import linear_model
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)#构造线性回归模型
print('Train Set of Score: %.2f' % regr.score(X_train, y_train))
print('Train Set of Score: %.2f' % regr.score(X_test, y_test))
#线性回归模型预测缺失值
regr.predict(pd.DataFrame(df.loc[4:6,"x"]))

#构建模型的训练集与测试集
df=pd.merge(pd.DataFrame(X,columns={
     'x'}),pd.DataFrame(Y,columns={
     'y'}),\
            left_index=True,right_index=True)
df.loc[4:6,"y"]=np.NaN#构造缺失值
X_train=pd.DataFrame(df.loc[21:100,'x'])
y_train=pd.DataFrame(df.loc[21:100,'y'])
X_test=pd.DataFrame(df.loc[10:20,'x'])
y_test=pd.DataFrame(df.loc[10:20,'y'])

#构建模型的训练集与测试集
df=pd.merge(pd.DataFrame(X,columns={
     'x'}),pd.DataFrame(Y,columns={
     'y'}),\
            left_index=True,right_index=True)
df.loc[4:6,"y"]=np.NaN#构造缺失值
X_train=pd.DataFrame(df.loc[21:100,'x'])
y_train=pd.DataFrame(df.loc[21:100,'y'])
X_test=pd.DataFrame(df.loc[10:20,'x'])
y_test=pd.DataFrame(df.loc[10:20,'y'])

#线性回归模型预测缺失值
regr.predict(pd.DataFrame(df.loc[4:6,"x"]))

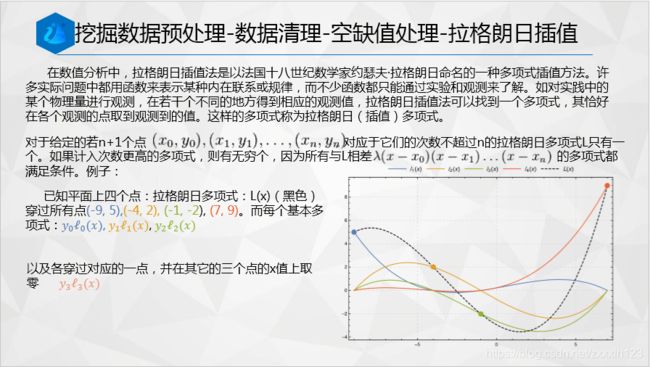
2.拉格朗日插值法

#拉格朗日插值法
import pandas as pd
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange
def polyinterp(data,k=5):
    df1=data.copy()
    print("原始数据(含缺失值）:",'\n',data)
    for i in range(len(df1)):
        if (df1['y'].isnull())[i]:
            #取数索引范围，向插值前取k个，向后取k个
            index_=list(range(i-k, i)) + list(range(i+1, i+1+k))#Series索引不为负数
            list0=[j for j in index_ if j in df1['y'].sort_index()]
            y= df1['y'][list0]
            #y= df1['y'][list(range(i-k, i)) + list(range(i+1, i+1+k))]
            y = y[y.notnull()]#索引为负则为缺失值，去掉缺失值
            f = lagrange(y.index, list(y))
            df1.iloc[i,1] = f(i)
    print("副本插值后:",'\n',df1)
    return(df1)
def chart_view(df01,df1):
    df1.rename(columns={
     'y': 'New y'}, inplace=True)
    df01['y'].plot(style='k--')
    df1['New y'].plot(alpha=0.5)
    plt.legend(loc='best')
    plt.show()
if __name__=='__main__':
    x=np.linspace(0,10,11)
    y=x**3+10
    data1=np.vstack((x,y))
    df0=pd.DataFrame(data1.T,columns=['x','y'])
    print(df0)
    df01=df0.copy()#建立副本
    df01.loc[2:3,"y"]=np.NaN#构造缺失值
    df1=df01.copy()
    
    new_data=polyinterp(df1,5)#插值后
    chart_view(df01,new_data)#插值前后绘图

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange
def polyinterp(data,k=5):
    df1=data.copy()
    print("原始数据(含缺失值）:",'\n',data)
    for i in range(len(df1)):
        if (df1['y'].isnull())[i]:
            #取数索引范围，向插值前取k个，向后取k个
            index_=list(range(i-k, i)) + list(range(i+1, i+1+k))#Series索引不为负数
            list0=[j for j in index_ if j in df1['y'].sort_index()]
            y= df1['y'][list0]
            y = y[y.notnull()]#索引为负则为缺失值，去掉缺失值
            f = lagrange(y.index, list(y))
            df1.iloc[i,1] = f(i)
    #print("副本插值后:",'\n',df1)
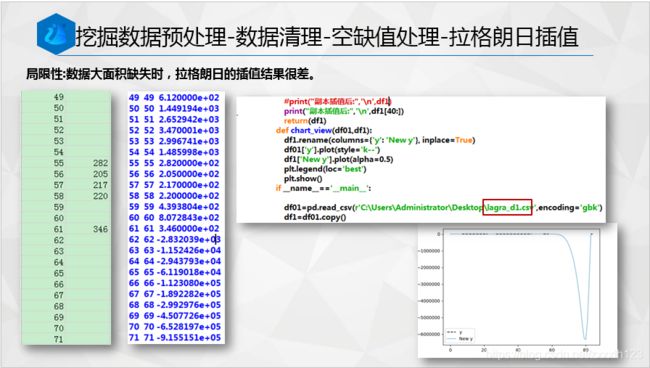
    print("副本插值后:",'\n',df1[40:])
    return(df1)
def chart_view(df01,df1):
    df1.rename(columns={
     'y': 'New y'}, inplace=True)
    df01['y'].plot(style='k--')
    df1['New y'].plot(alpha=0.5)
    plt.legend(loc='best')
    plt.show()
if __name__=='__main__':

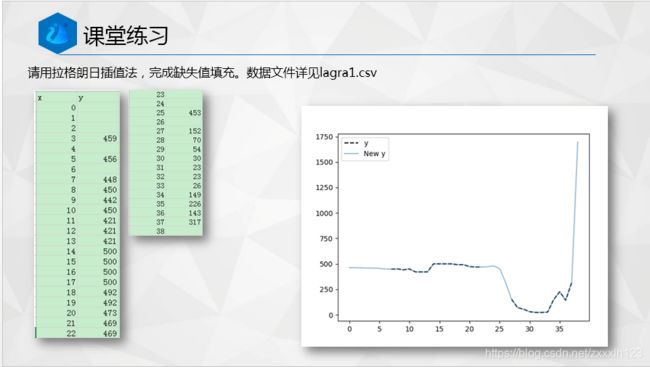
    df01=pd.read_csv(r'lagra_d1.csv',encoding='gbk')
    df1=df01.copy()
    
    new_data=polyinterp(df1,5)#插值后
    chart_view(df01,new_data)#插值前后绘图

编写打磨课件不易，走过路过别忘记给咱点个赞，小女子在此(❁´ω`❁)谢过！如需转载，请注明出处，Thanks♪(･ω･)ﾉ

参考文献：

1.https://blog.csdn.net/shener_m/article/details/81706358

2.https://blog.csdn.net/qq_20011607/article/details/81412985