Python实战——VAE的理论详解及Pytorch实现
参考的论文:
- Tutorial on Variational Autoencoders
- Auto-Encoding Variational Bayes
建议参考的文章:
- Pytorch里的CrossEntropyLoss详解
- 交叉熵的学习,有详细的理论以及Pytorch实现,欢迎Star
- Pytorch实现VAE 代码实现流程非常完整,可以看看这里面的VAE的结构图
- Pytorch入门之VAE这篇文章值得看的是里面对“稀疏编码”的介绍,然后代码中用到了卷积层,也不错
- PyTorch 实现 VAE 变分自编码器 含代码里面有自编码、卷积自编码以及变分自编码的结构图与代码,非常全面,强烈建议看看
模型引入
1.1 潜变量模型
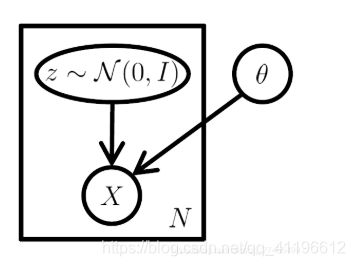
真实数据 X X X可能是高维的,并且依赖关系复杂,潜变量模型将问题按步骤分解:首先假设有一潜变量 z ∈ Z z\in Z z∈Z, Z Z Z是隐空间,易于根据概率密度函数 P ( z ) P(z) P(z)采样;其次,假定有一族函数 X ′ = f ( z ; θ ) X '= f ( z ; θ ) X′=f(z;θ) ,将 z z z映射为数据 X ′ X' X′。其中, z z z 为随机变量, θ \theta θ为固定参数, X ′ X' X′为与真实数据 X X X类似的"新"数据。
学习的目的就是要优化 θ \theta θ,目标为最大化真实数据 X X X的概率:
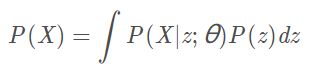
其中 P ( X ∣ z ; θ ) = N ( X ∣ f ( z , θ ) , σ 2 ∗ I ) P(X|z;\theta)=N(X|f(z,\theta),\sigma^2 * I) P(X∣z;θ)=N(X∣f(z,θ),σ2∗I)
注意到生成分布选择的是Guass分布。其他分布也可以,但需要满足: P ( X ∣ z ; θ ) P(X|z;θ) P(X∣z;θ)可计算且在 θ \theta θ处连续,这样我们才可通过梯度下降对其优化。
当不使用潜变量生成模型,直接取确定性的 X ′ = f ( z ; θ ) X' = f ( z ; θ ) X′=f(z;θ),相当于生成分布是一个Dirac delta分布,在 θ \theta θ上不连续。此时模型就是传统自编码器模型,它是点对点的,可以进行压缩降维,但不具备直接生成功能(其他未知的 z ′ z ′ z′对应的 X ′ X' X′ 是什么完全不清楚)。实际上,变分自编码器和传统自编码器只是在网络结构上有一定的相似之处,但本质完全不同。
1.2 变分自编码器
在潜变量模型的基础上,还需处理两个问题:
- P ( z ) P(z) P(z)的选择,事实上,任意 d d d维分布都可由 d d d个正态分布的变量通过足够复杂的函数映射而成,只需取 P ( z ) = N ( 0 , I ) P ( z ) = N ( 0 , I ) P(z)=N(0,I)即可,进一步的说明可参见原文。
- 将上面的优化目标 P ( X ) P ( X ) P(X)转化为可计算梯度的Loss Function,这就用到变分自编码器的另一个核心方法——变分法。
考虑直接使用蒙特卡洛方法: P ( X ) ≈ ∑ P ( z i ) P ( X ∣ z i ) P ( X ) ≈ \sum P(z_i) P(X|z_i ) P(X)≈∑P(zi)P(X∣zi),有两个弊端:
- 1)复杂的问题对于采样的样本量需求过大;
- 2)高斯分布设定下的极大似然度量等价于欧式平方距离,不满足复杂任务需求,对于这一点我们在文末给予详细讨论。
VAE通过改变采样过程同时解决以上两个弊端(在式(9)的推导过程中说了)。
模型搭建
2.1 设定优化目标
这一部分引入是因为一个问题:在通过采样的方法(蒙特卡洛法)计算下面这个式子的时候可不可以走捷径(shortcut)?
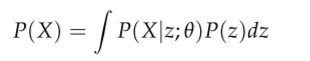
实际上(in practice),对大多数的潜变量 z z z而言, P ( X ∣ z ) P(X|z) P(X∣z)都是nearly zero的,因此它们对我们估计 P ( X ) P(X) P(X)是没啥用的。这个没啥用可以从两个角度来理解:
- 一方面,AE得到的隐变量是一个值,VAE把它拓展为一个分布,这可以看成是把点估计拓展为了一个区间估计。也就是说,在整个分布中其实只有一个区间是能够比较准确地反映样本 X X X的信息的,并且在区间估计中我们是希望区间越小越好的;
- 另一方面,我们有假定 P ( z ) P(z) P(z)服从 N ( 0 , I ) \mathcal{N(0,I)} N(0,I),但是就算是大数定律也只是说极限分布为某一个正态分布,而不一定是标准正态。也就是说,我们假设的 z z z的分布与实际之间存在一定的差异,这使得有用的 z z z的出现概率进一步降低。
这里就涉及到了VAE的核心思想了:尽量只采样那些对生成 X X X 有贡献的 z z z,然后用它们估计 P ( X ) P(X) P(X) 。
那么问题来了,从哪个分布里面去采样才能达到这个目的呢?
不妨假设 z z z从除了 N ( 0 , I ) \mathcal{N(0,I)} N(0,I)以外的某一个分布中采样,当然这么做会使计算更复杂。也就是说, z z z从任意一个除了 N ( 0 , I ) \mathcal{N(0,I)} N(0,I)以外的以 Q ( z ) Q(z) Q(z)为概率密度的分布(可以看作是 z z z的后验分布)中采样,在这里我们先假设分布是任意的去推导公式,最后再加条件简化推出来的优化目标。
分布有了,为假设的任意分布 Q ( z ) Q(z) Q(z),但是难免就会问啊,这个假设的分布与已知 X X X后 z z z的理想分布 P ( z ∣ X ) P(z|X) P(z∣X)相差大不大?我们的目标肯定是差距越小越好。你看,是不是找到了一个推导目标函数的切入点了?
所以为了实现这个目标,就有了下面的(2)式。那么为什么要推出(2)式右边部分呢?
- 一方面,理想分布 P ( z ∣ X ) P(z|X) P(z∣X)是未知的,我们得尽可能地把它替换为已知的量;
- 另一方面,前文也说了,(2)式左边只是一个切入点,我们肯定是希望从这个切入点着手得到上文说到的优化目标——最大化 P ( X ) P(X) P(X)。
首先,看一下 z z z的分布变化前后之间的差异。定义 P ( z ∣ X ) P(z|X) P(z∣X)与 Q ( z ) Q(z) Q(z)的Kullback-Leibler divergence(KL-divergence or D):(为什么要从这里开始?)
接着,通过使用贝叶斯将 P ( X ) P(X) P(X)和 P ( X ∣ z ) P(X|z) P(X∣z)代入上面的式子中得到:
变换一下式子,将可以由样本得到与不可由样本得到的部分分别放置在等式两端,得:
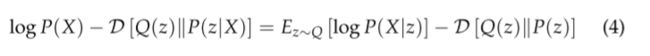
由于 X X X是固定的,已知的,而 Q Q Q分布我们假定为任意分布,那么为了更好地计算 Q ( z ) Q(z) Q(z),用 X X X构建分布 Q Q Q,也即 Q Q Q可以写成 Q ( z ∣ X ) Q(z|X) Q(z∣X),那么上式就变成了:
这个式子可以看作是VAE的basis。仔细观察上式:
- 左手边有我们想要最大化的量 P ( X ) P(X) P(X),再加上一个似乎很小且恒为正的项;
- 右手边称为 log P ( X ) \log P(X) logP(X)的 变分下界(variational lower bound or evidence lower bound, ELBO) ,是一个可以借助随机梯度下降 (Stochastic Gradient Descent, SGD) 优化的项(意味着 Q Q Q和 P ( z ) P(z) P(z)都得是连续的)。优化的内容是 Q Q Q,也就是说,我们通过训练分布 Q Q Q解决了 z z z的采样问题,同时还可以用训练得到的 Q Q Q预测哪些 z z z对生成 X X X是有益处的,而无需考虑其余的 z z z。
对eq. (5)中的变量的一点说明,比较容易搞混: P ( z ) P(z) P(z)是 z z z的先验分布, P ( z ∣ X ) P(z|X) P(z∣X)是 z z z的真实的后验分布, Q ( z ∣ X ) Q(z|X) Q(z∣X)是 z z z的近似后验分布; P ( X ) P(X) P(X)是 X X X的先验分布, P ( X ∣ z ) P(X|z) P(X∣z)是 X X X的后验分布。
Now for a bit more detail。
- 我们的目标是最大化 log P ( X ) \log P(X) logP(X)同时最小化 D [ Q ( z ∣ X ) ∣ ∣ P ( z ∣ X ) ] \mathcal{D}[Q(z | X) | | P(z | X)] D[Q(z∣X)∣∣P(z∣X)],其中 P ( z ∣ X ) P(z|X) P(z∣X)是无法解析计算的
- 左边第二项是用 Q ( z ∣ X ) Q(z|X) Q(z∣X)拟合 P ( z ∣ X ) P(z|X) P(z∣X),选取的 Q ( z ∣ X ) Q(z|X) Q(z∣X)期望上是要能很好地拟合 P ( z ∣ X ) P(z|X) P(z∣X)的,也即这个KL散度项是几乎为0的,那么优化目标也就变成了优化 log P ( X ) \log P(X) logP(X),这告诉了我们这个方法的一个好处:我们可以用 Q ( z ∣ x ) Q(z|x) Q(z∣x)计算 P ( z ∣ x ) P(z|x) P(z∣x)。
总结一下这部分的内容:我们想要最大化 P ( X ) P(X) P(X),但因为很多 z w i t h p . d . f P ( z ) z \ with \ p.d.f P(z) z with p.d.fP(z)没啥作用,因此找了个 z z z的后验分布 Q ( z ) Q(z) Q(z),最后又由于理想中后验分布 Q ( z ) Q(z) Q(z)与其先验分布 P ( z ) P(z) P(z)的差异很小,我们的优化目标就可以转变成:找到分布 Q ( z ) Q(z) Q(z),使得与 P ( X ) P(X) P(X)等价且和 Q ( z ) Q(z) Q(z)有关的那部分( 即式(5)的右部 )最大。
2.2 离散化优化目标
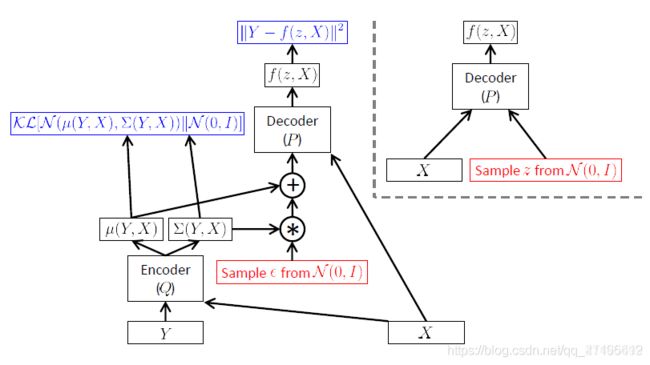
我们应该怎么应用SGD优化等式右边呢?首先肯定得指定 Q ( z ∣ X ) Q(z|X) Q(z∣X)的分布形式,为了计算方便,不妨假设它为一个多元正态分布: Q ( z ∣ X ) = N ( z ∣ μ ( X ; ϑ ) , Σ ( X ; ϑ ) ) Q(z|X) = \mathcal{N}(z | \mu(X ; \vartheta), \Sigma(X ; \vartheta)) Q(z∣X)=N(z∣μ(X;ϑ),Σ(X;ϑ)),其中 μ \mu μ和 Σ \Sigma Σ任意的关于 ϑ \vartheta ϑ(可以从数据中学习到)的函数。实际上,可以通过神经网络得到 μ \mu μ和 Σ \Sigma Σ,并且还可以把 Σ \Sigma Σ约束为对角矩阵,这么做主要是为了计算方便。
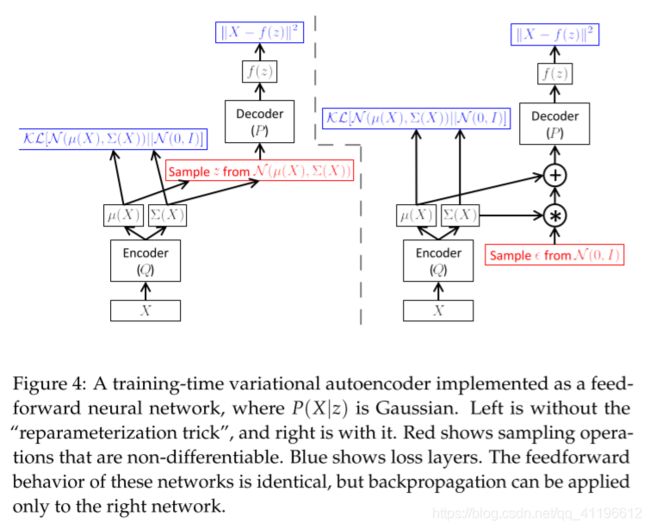
对上图的解释:在BP的过程中,误差需要穿过一个采样层,该操作不连续且没有梯度。SGD可以处理随机输入,但不能处理随机操作!解决方法称为 “重新参数化”,如上图右侧所示。先采样 ϵ ∼ N ( 0 , I ) \epsilon\sim N(0,I) ϵ∼N(0,I),然后令 z = μ ( X ) + Σ 1 / 2 ( X ) ∗ ϵ z=\mu(X)+\Sigma^{1/2}(X)*\epsilon z=μ(X)+Σ1/2(X)∗ϵ。所以“重参数化”的目的就是为了让模型可以求导,进而可以用SGD求解。
现在开始正式将优化目标转为可以计算的形式。
KL散度部分的化简(这部分也称作正则项)
在我们的优化目标那个等式中,等式右边有一个衡量两个正态分布差异性的KL散度。一般地,两个多元正态分布的KL散度可以表示成:(想看两个多元正态分布KL散度的推导点这里,主要用到了迹的性质:可与期望交换且tr(AB)=tr(BA))
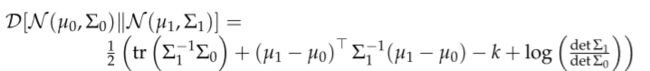
其中 k k k是分布的维度。因此在上文推出的那个式子中的KL散度就可以化简为:
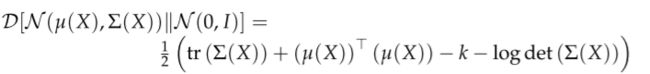
非常有必要说明的是,由于我们有约束隐变量的分布向标准正态靠近,因此理论上最优的时候 Σ \Sigma Σ应该是对角矩阵,也就是说,我们只需要采样获得对角线上的 k k k的数据所组成的向量就行了,不妨记该向量为 σ 2 = ( σ 1 2 , σ 2 2 , ⋯ , σ k 2 ) \sigma^2=(\sigma^2_1,\sigma^2_2,\cdots,\sigma^2_k) σ2=(σ12,σ22,⋯,σk2),那么有 t r ( Σ ) = ∑ i = 1 k σ i 2 tr(\Sigma)=\sum\limits_{i=1}^{k}\sigma^2_i tr(Σ)=i=1∑kσi2, d e t ( Σ ) = ∏ i = 1 k σ i 2 det(\Sigma)=\prod\limits_{i=1}^{k}\sigma^2_i det(Σ)=i=1∏kσi2。
那么,这一部分为什么要约束我们生成的latent variable的分布向正态分布看齐呢?
主要有两个原因:
- 保留住方差信息,使VAE不至于退化成AE;
- 保证模型的“生成能力”。
下面分别来解释这两个原因。
首先,我们希望重构 X X X,也就是最小化 D ( X ^ k , X k ) 2 D(X̂_k,X_k)^2 D(X^k,Xk)2,但是这个重构过程受到噪声的影响,因为 z k z_k zk 是通过重新采样过的,不是直接由 encoder 算出来的。
显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为 0 的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。说白了,模型会慢慢退化成普通的 AutoEncoder,噪声不再起作用。
这样不就白费力气了吗?说好的生成模型呢?别急别急,其实 VAE 还让所有的 P ( z ∣ X ) P(z|X) P(z∣X) 都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢?如果所有的 P ( z ∣ X ) P(z|X) P(z∣X) 都很接近标准正态分布 N ( 0 , I ) N(0,I) N(0,I),那么根据定义:
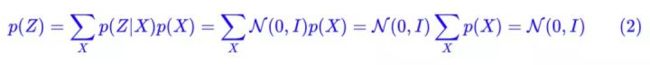
这样我们就能达到我们的先验假设: P ( z ) P(z) P(z) 是标准正态分布。然后我们就可以放心地从 N ( 0 , I ) N(0,I) N(0,I) 中采样来生成图像了。
期望部分的简化(这部分也称为重构误差项)
仔细观察一下这部分的结构:已知隐变量 z z z,得到原样本的概率。假设一下,如果这个概率越大,是不是意味着decoder的输出与 X X X的差异越小,而差异我们可以怎么衡量?
由于 X X X与其重构量 X ′ X' X′都是向量,因此其中一个办法是直接计算两者之间的平均距离,即MSE。但是MSE在某些特定情况下从理论上来说是没有交叉熵*(Cross Entropy, CE)*好的(对这部分感兴趣的话可以到我的GitHub上看一下:链接, 欢迎star ^ - ^)
然后好巧不巧的是,在decoder的输出分布为二项分布的时候,重构误差项刚好就是二元交叉熵 (Binary Cross-Entropy, BCE),简直太神奇了(推导见这一小节的最后部分)。
这部分我们可以用采样的方式来估计,有点像是蒙特卡洛方法。
首先,前面讲到的优化目标其实是对一个 X X X而言的,而我们一般会有很多个 X X X,不妨设这些 X X X的定义域为 D D D,即有 X ∈ D X \in D X∈D,那么上面推出来的优化目标就要有所改变了:
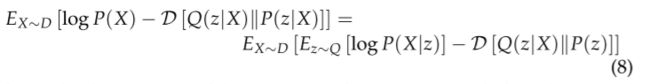
也即对 X X X再求一个期望。我们可以从 Q ( z ∣ X ) Q(z|X) Q(z∣X)从采样获得单个的 z z z或者 X X X,计算以下梯度:
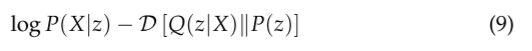
然后我们可以使用采样得到的任意多的样本 X X X和 z z z对(9)式取平均值(先对 z z z求平均,再对 X X X求平均),那么这么平均值显然是收敛到(8)式的。
但是(9)式是有点问题的,因为从
![]()
我们可以看出优化目标应该是由 P P P和 Q Q Q共同决定的,但是如果我们按照(9)式去采样离散化,其中(9)式的第一部分是不受 Q Q Q的影响的(因为前面说过为了让模型可以用SGD,我们是从标准正态分布中采样 z z z的,而不是从 Q Q Q里面),这就有问题了。
论文中给出的方案是这样的:修改(8)式右边的第一部分,尽可能让其不依赖于 Q Q Q,而是依赖于标准正态分布,怎么办?“重参数化”!
通过观察2.2节最开始我放的那个图,我们将从 Q Q Q中采样转变成了从标准正态分布中采样,这里就不多说了,上面已经说的蛮详细了。因此(8)式就变成了:
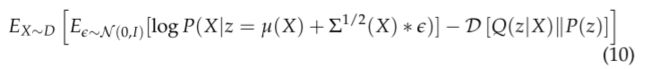
仔细看一下上式,如果我们要对参数 μ \mu μ和 Σ \Sigma Σ求偏导的话,偏导符号是可以直接放到期望符号里面的。也就是说,一旦确定下 X X X和 ϵ \epsilon ϵ,整个目标函数就被确定下来了,并且还是关于 P P P和 Q Q Q分布连续的(如果 P P P和 Q Q Q连续的话)。
其实看到这里之后是不是仍然懵逼,不知道具体该怎么算?那就对了,接下来我再讲讲具体该如何计算 log P ( X ∣ z ) \log P(X|z) logP(X∣z)。
先给出变分贝叶斯论文上的一部分说明,论文原文见本篇博客最开始给的链接。

再给出我的一点阅读笔记:

这里面的C.2部分我刚开始看的有点迷糊,为什么最后的 μ \mu μ个 σ \sigma σ不用放到激活函数里呢?毕竟这是一个MLP。后来看到了下面两张图,瞬间明白了:
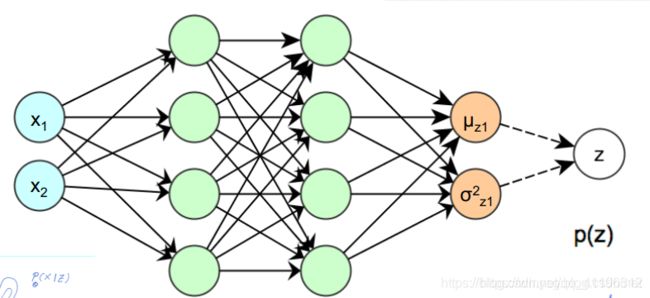
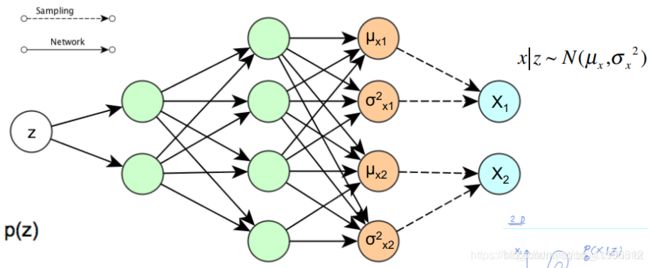
如果decoder部分的输出是一个正态分布,那么结果按照C.2对应的步骤计算,相应的量也都有了,因此我就不多说了。
但如果输出的是一个伯努利分布,需要另外说明一下。有时候我们需要decoder输出图片向量,而不是均值和方差,那这时候其实就是默认的输出为伯努利分布,同时有下面的结论:
log p ( X ∣ z ) = ∑ i = 1 D x i log y i + ( 1 − x i ) log ( 1 − y i ) = B C E \log p(X|z) = \sum \limits_{i=1}^{D}x_i \log y_i + (1-x_i) \log (1-y_i) =BCE logp(X∣z)=i=1∑Dxilogyi+(1−xi)log(1−yi)=BCE
其中变量的解释见这一小节的上面给出的论文的截图。
2.2的补充
这一节内容摘自知乎,链接为:知乎参照文章链接
框架的示意图如下(错误的示意图):
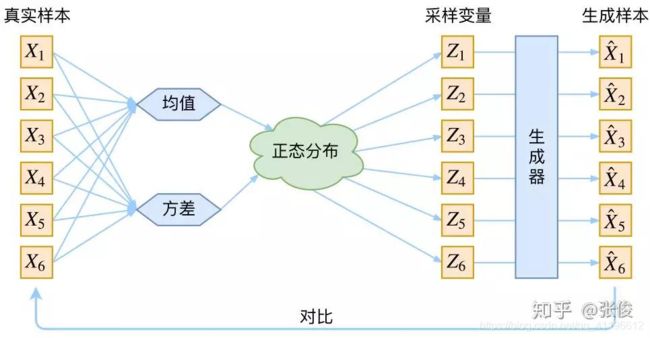
看出了什么问题了吗?如果像这个图的话,我们其实完全不清楚:究竟经过重新采样出来的 z k z_k zk,是不是还对应着原来的 X k X_k Xk,所以我们如果直接最小化 D ( X ^ k , X k ) 2 D(X̂_k,X_k)^2 D(X^k,Xk)2(这里 D D D 代表某种距离函数)是很不科学的,而事实上你看代码也会发现根本不是这样实现的。
具体来说,给定一个真实样本 X k X_k Xk,我们假设存在一个专属于 X k X_k Xk 的分布 P ( z ∣ X k ) P(z|X_k) P(z∣Xk)(学名叫后验分布),并进一步假设这个分布是(独立的、多元的)正态分布。
为什么要强调“专属”呢?因为我们后面要训练一个生成器 X = g ( z ) X=g(z) X=g(z),希望能够把从分布 P ( z ∣ X k ) P(z|X_k) P(z∣Xk) 采样出来的一个 z k z_k zk 还原为 X k X_k Xk。
如果假设 P ( z ) P(z) P(z) 是正态分布,然后从 P ( z ) P(z) P(z) 中采样一个 z z z,那么我们怎么知道这个 z z z 对应于哪个真实的 X X X 呢?现在 P ( z ∣ X k ) P(z|X_k) P(z∣Xk) 专属于 X k X_k Xk,我们有理由说从这个分布采样出来的 z z z 应该要还原到 X k X_k Xk 中去。
再次强调,这时候每一个 X k X_k Xk 都配上了一个专属的正态分布,才方便后面的生成器做还原。但这样有多少个 X X X 就有多少个正态分布了。我们知道正态分布有两组参数:均值 μ μ μ 和方差 σ 2 σ^2 σ2(多元的话,它们都是向量)。
那我怎么找出专属于 Xk 的正态分布 p(Z|Xk) 的均值和方差呢?好像并没有什么直接的思路。
那好吧,我就用神经网络来拟合出来。这就是神经网络时代的哲学:难算的我们都用神经网络来拟合,在 WGAN 那里我们已经体验过一次了,现在再次体验到了。
于是我们构建两个神经网络 μ k = f 1 ( X k ) μ_k=f_1(X_k) μk=f1(Xk), log σ k 2 = f 2 ( X k ) \logσ_k^2=f_2(X_k) logσk2=f2(Xk) 来算它们。我们选择拟合 log σ k 2 \logσ_k^2 logσk2 而不是直接拟合 σ k 2 σ_k^2 σk2,是因为 σ k 2 σ_k^2 σk2 总是非负的,需要加激活函数处理,而拟合 log σ k 2 \logσ_k^2 logσk2 不需要加激活函数,因为它可正可负。
到这里,我能知道专属于 X k X_k Xk 的均值和方差了,也就知道它的正态分布长什么样了,然后从这个专属分布中采样一个 z k z_k zk 出来,然后经过一个生成器(decoder)得到 X ^ k = g ( z k ) X̂_k=g(z_k) X^k=g(zk)。于是可以画出 VAE 的示意图:
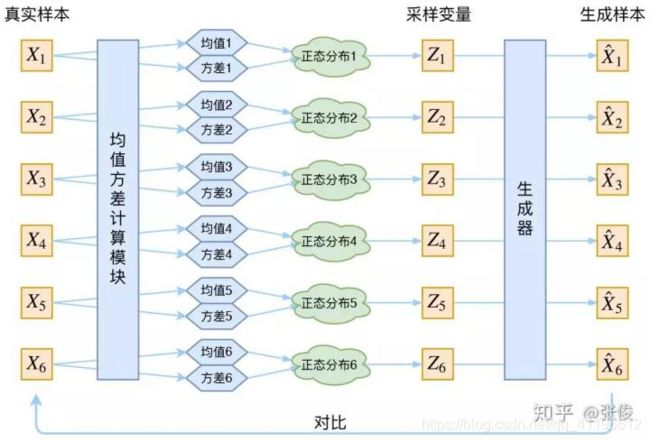
事实上,VAE 是为每个样本构造专属的正态分布,然后采样来重构。
2.3 生成&测试
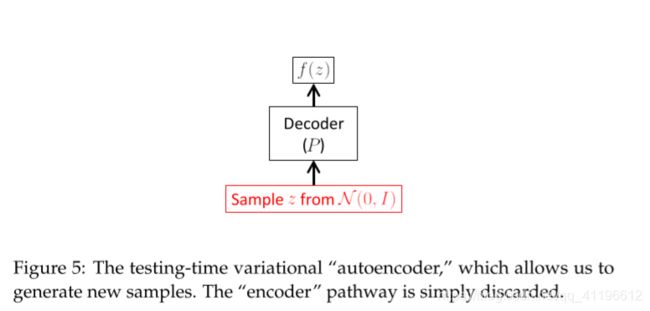
在生成与测试这一块,我们可以直接省去可能使 z z z的分布发生改变的encoder部分,而直接使用decoder部分,相关流程图如下:
3 条件变分自编码器(CVAE)
将上述VAE推广到多模态,优化目标从 P ( Y ) P(Y) P(Y)变成 P ( Y ∣ X ) P ( Y ∣ X ) P(Y∣X)(这里对 X X X, Y Y Y进行了重新定义)
4 关于相似性度量
一句话,相似性度量决定了生成模型在生成新样本时,新样本与原样本微小差异的方向。
例如简单的潜变量模型,采用平方距离度量,在生成新样本时,就倾向于产生与原样本具有较小平方距离的新样本。如下图所示,a为原样本,b c为新样本,b与a的平方距离更小(c是a的图像整体平移得到的)。
在生成过程中,简单的潜变量模型就更倾向于生成b而不是c。这与我们的直观印象是相悖的,往往需要根据经验和具体问题来人为设计相似性度量。

VAE是如何解决这个问题的?VAE给直接采样过程加入了新的信息,就是模拟后验分布 Q ( z ∣ X ) Q(z|X) Q(z∣X),生成样本的时候就不是在潜变量 z z z的整个空间采样(通过 P ( z ) P(z) P(z)),而是在其子空间(通过 Q ( z ∣ X ) Q(z|X) Q(z∣X))采样。
从模型的解释性上来说,潜变量 z z z存储的就是类似于数字,角度,位置,线条粗细,风格等类似的一系列潜在因素。
从优化目标来看,要同时最大化 log P ( X ) \log P(X) logP(X)和最小化 D [ Q ( z ∣ X ) ∣ ∣ P ( z ∣ X ) ] D[Q(z|X)||P(z|X)] D[Q(z∣X)∣∣P(z∣X)],对子空间的精确限制就是在避免(b)这种不合理清形的出现(因为b的分布与a不一致)。
另一方面,从优化目标的计算形式来看(虽然不是非常精确,但也能窥到一些端倪),要同时最小化平方距离和 D [ Q ( z ∣ X ) ∣ ∣ P ( z ) ] D[Q(z|X)||P(z)] D[Q(z∣X)∣∣P(z)],也就是说既要新样本在平方距离上接近,同时也要潜空间上引入的信息量更小。
对于样本b来说,虽然平方距离上接近,但是要生成这样的样本,潜空间上的决定因素和a差异很大,而c在潜空间上和a的一致性更高。从而,VAE更倾向于生成c而非b。
总之,简单的潜变量模型对 z z z所在因素空间的划分是只以平方距离为导向的、平均化的、混乱的,使得非a所属子因素空间内的 z z z强行生成,最后得到了b。而VAE为每个样本划分了专属的子因素空间,使得各自子因素空间内的 z z z只致力于生成对应的 X ′ X ′ X′,同时 D [ Q ( z ∣ X ) ∣ ∣ P ( z ∣ X ) ] D[Q(z|X)||P(z|X)] D[Q(z∣X)∣∣P(z∣X)]的优化约束保证了子因素空间划分的合理性。
4 总结
- AE是点对点模型,生成没有任何数学保证;
- 潜变量模型强行用其他潜因素生成目标,只保证平方距离小,风格差异大;
- VAE优化目标左侧,既要生成概率大,又要模拟后验分布精准(潜空间合理划分)
- VAE优化目标右侧,b平方loss小而 D [ Q ( z ∣ X ) ∣ ∣ P ( z ) ] D[Q(z|X)||P(z)] D[Q(z∣X)∣∣P(z)]loss大,c平方loss大而 D [ Q ( z ∣ X ) ∣ ∣ P ( z ) ] D[Q(z|X)||P(z)] D[Q(z∣X)∣∣P(z)]loss小。
5 代码实现
5.1 AE
- main.py
import torch
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from ae import AE
from torch import nn, optim
import matplotlib.pyplot as plt
plt.style.use("ggplot")
def main(epoch_num):
# 下载mnist数据集
mnist_train = datasets.MNIST('mnist', train=True, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
mnist_test = datasets.MNIST('mnist', train=False, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
# 载入mnist数据集
# batch_size设置每一批数据的大小,shuffle设置是否打乱数据顺序,结果表明,该函数会先打乱数据再按batch_size取数据
mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)
mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)
# 查看每一个batch图片的规模
x, label = iter(mnist_train).__next__() # 取出第一批(batch)训练所用的数据集
print(' img : ', x.shape) # img : torch.Size([32, 1, 28, 28]), 每次迭代获取32张图片,每张图大小为(1,28,28)
# 准备工作 : 搭建计算流程
device = torch.device('cuda')
model = AE().to(device) # 生成AE模型,并转移到GPU上去
print('The structure of our model is shown below: \n')
print(model)
loss_function = nn.MSELoss() # 生成损失函数
optimizer = optim.Adam(model.parameters(), lr=1e-3) # 生成优化器,需要优化的是model的参数,学习率为0.001
# 开始迭代
loss_epoch = []
for epoch in range(epoch_num):
# 每一代都要遍历所有的批次
for batch_index, (x, _) in enumerate(mnist_train):
# [b, 1, 28, 28]
x = x.to(device)
# 前向传播
x_hat = model(x) # 模型的输出,在这里会自动调用model中的forward函数
loss = loss_function(x_hat, x) # 计算损失值,即目标函数
# 后向传播
optimizer.zero_grad() # 梯度清零,否则上一步的梯度仍会存在
loss.backward() # 后向传播计算梯度,这些梯度会保存在model.parameters里面
optimizer.step() # 更新梯度,这一步与上一步主要是根据model.parameters联系起来了
loss_epoch.append(loss.item())
if epoch % (epoch_num // 10) == 0:
print('Epoch [{}/{}] : '.format(epoch, epoch_num), 'loss = ', loss.item()) # loss是Tensor类型
# x, _ = iter(mnist_test).__next__() # 在测试集中取出一部分数据
# with torch.no_grad():
# x_hat = model(x)
return loss_epoch
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
epoch_num = 100
loss_epoch = main(epoch_num=epoch_num)
# 绘制迭代结果
plt.plot(loss_epoch)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
- ae.py
from torch import nn
class AE(nn.Module):
def __init__(self):
# 调用父类方法初始化模块的state
super(AE, self).__init__()
# 编码器 : [b, 784] => [b, 20]
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 20),
nn.ReLU()
)
# 解码器 : [b, 20] => [b, 784]
self.decoder = nn.Sequential(
nn.Linear(20, 256),
nn.ReLU(),
nn.Linear(256, 784),
nn.Sigmoid() # 图片数值取值为[0,1],不宜用ReLU
)
def forward(self, x):
"""
向前传播部分, 在model_name(inputs)时自动调用
:param x: the input of our training model
:return: the result of our training model
"""
batch_size = x.shape[0] # 每一批含有的样本的个数
# flatten
# tensor.view()方法可以调整tensor的形状,但必须保证调整前后元素总数一致。view不会修改自身的数据,
# 返回的新tensor与原tensor共享内存,即更改一个,另一个也随之改变。
x = x.view(batch_size, 784) # 一行代表一个样本
# encoder
x = self.encoder(x)
# decoder
x = self.decoder(x)
# reshape
x = x.view(batch_size, 1, 28, 28)
return x
5.2 VAE
- main.py
import torch
from torch import optim
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from torchvision.utils import save_image
from vae import VAE
import matplotlib.pyplot as plt
import argparse
import os
import shutil
import numpy as np
# plt.style.use("ggplot")
# 设置模型运行的设备
cuda = torch.cuda.is_available()
device = torch.device("cuda" if cuda else "cpu")
# 设置默认参数
parser = argparse.ArgumentParser(description="Variational Auto-Encoder MNIST Example")
parser.add_argument('--result_dir', type=str, default='./VAEResult', metavar='DIR', help='output directory')
parser.add_argument('--save_dir', type=str, default='./checkPoint', metavar='N', help='model saving directory')
parser.add_argument('--batch_size', type=int, default=128, metavar='N', help='batch size for training(default: 128)')
parser.add_argument('--epochs', type=int, default=200, metavar='N', help='number of epochs to train(default: 200)')
parser.add_argument('--seed', type=int, default=1, metavar='S', help='random seed(default: 1)')
parser.add_argument('--resume', type=str, default='', metavar='PATH', help='path to latest checkpoint(default: None)')
parser.add_argument('--test_every', type=int, default=10, metavar='N', help='test after every epochs')
parser.add_argument('--num_worker', type=int, default=1, metavar='N', help='the number of workers')
parser.add_argument('--lr', type=float, default=1e-3, help='learning rate(default: 0.001)')
parser.add_argument('--z_dim', type=int, default=20, metavar='N', help='the dim of latent variable z(default: 20)')
parser.add_argument('--input_dim', type=int, default=28 * 28, metavar='N', help='input dim(default: 28*28 for MNIST)')
parser.add_argument('--input_channel', type=int, default=1, metavar='N', help='input channel(default: 1 for MNIST)')
args = parser.parse_args()
kwargs = {
'num_workers': 2, 'pin_memory': True} if cuda else {
}
def dataloader(batch_size=128, num_workers=2):
transform = transforms.Compose([
transforms.ToTensor(),
])
# 下载mnist数据集
mnist_train = datasets.MNIST('mnist', train=True, transform=transform, download=True)
mnist_test = datasets.MNIST('mnist', train=False, transform=transform, download=True)
# 载入mnist数据集
# batch_size设置每一批数据的大小,shuffle设置是否打乱数据顺序,结果表明,该函数会先打乱数据再按batch_size取数据
# num_workers设置载入输入所用的子进程的个数
mnist_train = DataLoader(mnist_train, batch_size=batch_size, shuffle=True)
mnist_test = DataLoader(mnist_test, batch_size=batch_size, shuffle=True)
classes = ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9')
return mnist_test, mnist_train, classes
def loss_function(x_hat, x, mu, log_var):
"""
Calculate the loss. Note that the loss includes two parts.
:param x_hat:
:param x:
:param mu:
:param log_var:
:return: total loss, BCE and KLD of our model
"""
# 1. the reconstruction loss.
# We regard the MNIST as binary classification
BCE = F.binary_cross_entropy(x_hat, x, reduction='sum')
# 2. KL-divergence
# D_KL(Q(z|X) || P(z)); calculate in closed form as both dist. are Gaussian
# here we assume that \Sigma is a diagonal matrix, so as to simplify the computation
KLD = 0.5 * torch.sum(torch.exp(log_var) + torch.pow(mu, 2) - 1. - log_var)
# 3. total loss
loss = BCE + KLD
return loss, BCE, KLD
def save_checkpoint(state, is_best, outdir):
"""
每训练一定的epochs后, 判断损失函数是否是目前最优的,并保存模型的参数
:param state: 需要保存的参数,数据类型为dict
:param is_best: 说明是否为目前最优的
:param outdir: 保存文件夹
:return:
"""
if not os.path.exists(outdir):
os.makedirs(outdir)
checkpoint_file = os.path.join(outdir, 'checkpoint.pth') # join函数创建子文件夹,也就是把第二个参数对应的文件保存在'outdir'里
best_file = os.path.join(outdir, 'model_best.pth')
torch.save(state, checkpoint_file) # 把state保存在checkpoint_file文件夹中
if is_best:
shutil.copyfile(checkpoint_file, best_file)
def test(model, optimizer, mnist_test, epoch, best_test_loss):
test_avg_loss = 0.0
with torch.no_grad(): # 这一部分不计算梯度,也就是不放入计算图中去
'''测试测试集中的数据'''
# 计算所有batch的损失函数的和
for test_batch_index, (test_x, _) in enumerate(mnist_test):
test_x = test_x.to(device)
# 前向传播
test_x_hat, test_mu, test_log_var = model(test_x)
# 损害函数值
test_loss, test_BCE, test_KLD = loss_function(test_x_hat, test_x, test_mu, test_log_var)
test_avg_loss += test_loss
# 对和求平均,得到每一张图片的平均损失
test_avg_loss /= len(mnist_test.dataset)
'''测试随机生成的隐变量'''
# 随机从隐变量的分布中取隐变量
z = torch.randn(args.batch_size, args.z_dim).to(device) # 每一行是一个隐变量,总共有batch_size行
# 对隐变量重构
random_res = model.decode(z).view(-1, 1, 28, 28)
# 保存重构结果
save_image(random_res, './%s/random_sampled-%d.png' % (args.result_dir, epoch + 1))
'''保存目前训练好的模型'''
# 保存模型
is_best = test_avg_loss < best_test_loss
best_test_loss = min(test_avg_loss, best_test_loss)
save_checkpoint({
'epoch': epoch, # 迭代次数
'best_test_loss': best_test_loss, # 目前最佳的损失函数值
'state_dict': model.state_dict(), # 当前训练过的模型的参数
'optimizer': optimizer.state_dict(),
}, is_best, args.save_dir)
return best_test_loss
def main():
# Step 1: 载入数据
mnist_test, mnist_train, classes = dataloader(args.batch_size, args.num_worker)
# 查看每一个batch图片的规模
x, label = iter(mnist_train).__next__() # 取出第一批(batch)训练所用的数据集
print(' img : ', x.shape) # img : torch.Size([batch_size, 1, 28, 28]), 每次迭代获取batch_size张图片,每张图大小为(1,28,28)
# Step 2: 准备工作 : 搭建计算流程
model = VAE(z_dim=args.z_dim).to(device) # 生成AE模型,并转移到GPU上去
print('The structure of our model is shown below: \n')
print(model)
optimizer = optim.Adam(model.parameters(), lr=args.lr) # 生成优化器,需要优化的是model的参数,学习率为0.001
# Step 3: optionally resume(恢复) from a checkpoint
start_epoch = 0
best_test_loss = np.finfo('f').max
if args.resume:
if os.path.isfile(args.resume):
# 载入已经训练过的模型参数与结果
print('=> loading checkpoint %s' % args.resume)
checkpoint = torch.load(args.resume)
start_epoch = checkpoint['epoch'] + 1
best_test_loss = checkpoint['best_test_loss']
model.load_state_dict(checkpoint['state_dict'])
optimizer.load_state_dict(checkpoint['optimizer'])
print('=> loaded checkpoint %s' % args.resume)
else:
print('=> no checkpoint found at %s' % args.resume)
if not os.path.exists(args.result_dir):
os.makedirs(args.result_dir)
# Step 4: 开始迭代
loss_epoch = []
for epoch in range(start_epoch, args.epochs):
# 训练模型
# 每一代都要遍历所有的批次
loss_batch = []
for batch_index, (x, _) in enumerate(mnist_train):
# x : [b, 1, 28, 28], remember to deploy the input on GPU
x = x.to(device)
# 前向传播
x_hat, mu, log_var = model(x) # 模型的输出,在这里会自动调用model中的forward函数
loss, BCE, KLD = loss_function(x_hat, x, mu, log_var) # 计算损失值,即目标函数
loss_batch.append(loss.item()) # loss是Tensor类型
# 后向传播
optimizer.zero_grad() # 梯度清零,否则上一步的梯度仍会存在
loss.backward() # 后向传播计算梯度,这些梯度会保存在model.parameters里面
optimizer.step() # 更新梯度,这一步与上一步主要是根据model.parameters联系起来了
# print statistics every 100 batch
if (batch_index + 1) % 100 == 0:
print('Epoch [{}/{}], Batch [{}/{}] : Total-loss = {:.4f}, BCE-Loss = {:.4f}, KLD-loss = {:.4f}'
.format(epoch + 1, args.epochs, batch_index + 1, len(mnist_train.dataset) // args.batch_size,
loss.item() / args.batch_size, BCE.item() / args.batch_size,
KLD.item() / args.batch_size))
if batch_index == 0:
# visualize reconstructed result at the beginning of each epoch
x_concat = torch.cat([x.view(-1, 1, 28, 28), x_hat.view(-1, 1, 28, 28)], dim=3)
save_image(x_concat, './%s/reconstructed-%d.png' % (args.result_dir, epoch + 1))
# 把这一个epoch的每一个样本的平均损失存起来
loss_epoch.append(np.sum(loss_batch) / len(mnist_train.dataset)) # len(mnist_train.dataset)为样本个数
# 测试模型
if (epoch + 1) % args.test_every == 0:
best_test_loss = test(model, optimizer, mnist_test, epoch, best_test_loss)
return loss_epoch
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
loss_epoch = main()
# 绘制迭代结果
plt.plot(loss_epoch)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
- vae.py
from torch import nn
import torch
import torch.nn.functional as F
class VAE(nn.Module):
def __init__(self, input_dim=784, h_dim=400, z_dim=20):
# 调用父类方法初始化模块的state
super(VAE, self).__init__()
self.input_dim = input_dim
self.h_dim = h_dim
self.z_dim = z_dim
# 编码器 : [b, input_dim] => [b, z_dim]
self.fc1 = nn.Linear(input_dim, h_dim) # 第一个全连接层
self.fc2 = nn.Linear(h_dim, z_dim) # mu
self.fc3 = nn.Linear(h_dim, z_dim) # log_var
# 解码器 : [b, z_dim] => [b, input_dim]
self.fc4 = nn.Linear(z_dim, h_dim)
self.fc5 = nn.Linear(h_dim, input_dim)
def forward(self, x):
"""
向前传播部分, 在model_name(inputs)时自动调用
:param x: the input of our training model [b, batch_size, 1, 28, 28]
:return: the result of our training model
"""
batch_size = x.shape[0] # 每一批含有的样本的个数
# flatten [b, batch_size, 1, 28, 28] => [b, batch_size, 784]
# tensor.view()方法可以调整tensor的形状,但必须保证调整前后元素总数一致。view不会修改自身的数据,
# 返回的新tensor与原tensor共享内存,即更改一个,另一个也随之改变。
x = x.view(batch_size, self.input_dim) # 一行代表一个样本
# encoder
mu, log_var = self.encode(x)
# reparameterization trick
sampled_z = self.reparameterization(mu, log_var)
# decoder
x_hat = self.decode(sampled_z)
# reshape
x_hat = x_hat.view(batch_size, 1, 28, 28)
return x_hat, mu, log_var
def encode(self, x):
"""
encoding part
:param x: input image
:return: mu and log_var
"""
h = F.relu(self.fc1(x))
mu = self.fc2(h)
log_var = self.fc3(h)
return mu, log_var
def reparameterization(self, mu, log_var):
"""
Given a standard gaussian distribution epsilon ~ N(0,1),
we can sample the random variable z as per z = mu + sigma * epsilon
:param mu:
:param log_var:
:return: sampled z
"""
sigma = torch.exp(log_var * 0.5)
eps = torch.randn_like(sigma)
return mu + sigma * eps # 这里的“*”是点乘的意思
def decode(self, z):
"""
Given a sampled z, decode it back to image
:param z:
:return:
"""
h = F.relu(self.fc4(z))
x_hat = torch.sigmoid(self.fc5(h)) # 图片数值取值为[0,1],不宜用ReLU
return x_hat