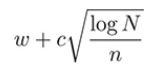翻译Deep Learning and the Game of Go（6）第4章(下)蒙特卡洛树搜索在围棋上的使用，改进评估函数

注：该文章接上一篇文章，同样是原书第4章内容

4.5 使用蒙特卡洛树搜索来评估棋盘状态

         在alpha-Beta剪枝中，你使用了一个盘面评估函数来帮助你减少必须考虑的盘面数量。但是围棋中的盘面评估是非常，非常困难的：你的基于吃子的简单评估函数不会愚弄很多围棋玩家。蒙特卡洛树搜索提供了一种在没有任何关于游戏的战略知识的情况下评估游戏状态的方法，该蒙特卡洛算法通过模拟随机游戏来评估一个位置好不好。这些随机游戏中的一种叫做rollout或playout。在这本书中，我们使用了rollout一词。

        蒙特卡罗树搜索是蒙特卡罗算法大家族的一部分，它利用随机性来分析极其复杂的情况，其名字的一个来源就是去摩纳哥著名的赌场区。

       这可能看起来通过随机选择无法制定一个好的策略。一款完全随机落子的游戏AI当然非常弱，但当你让两各随机的AI互相对抗时，对手也同样是很笨的。如果黑棋总是比白棋赢得多，那一定是因为黑棋一开始取得了优势，因此，如果你想判断是否下在这点能够使你取得优势，可以采用这种评估方法，而你不需要理解为什么这个落子点是好的。

它有可能会得到不平衡的结果。如果你模拟10场随机游戏，白赢了7场，你会有多自信觉得白棋取得优势？不是很好：白棋只比拟预料的多赢了两场。如果黑棋和白棋是完全平衡的，那么大约有30%的机会看到7/10的结果。另一方面，如果白棋在100场随机比赛中赢得70场，你可以几乎可以肯定的是，评估开始的位置确实对白棋有利。关键的是，当你随机对弈更多时，你的评估会变得更准确

每次蒙特卡洛算法分三步：

     1.在蒙特卡洛树中添加一个新的棋盘盘面。

     2.从那个位置模拟一个随机对局。

     3.更新树的关于随机游戏结果的统计数据。

如果你的时间允许，你尽可以重复以上过程多次，然后根据树顶的统计数据告诉你该选哪一个。

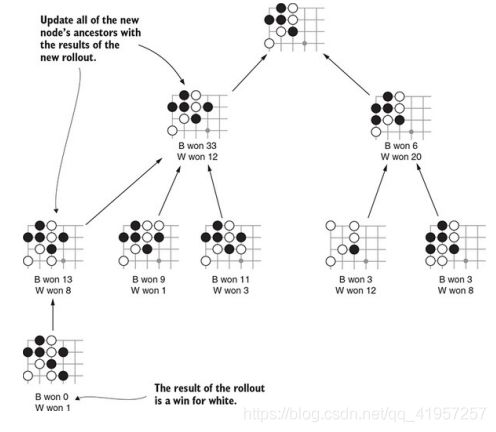
让我们来尝试一轮的蒙特卡洛算法。下图显示了蒙特卡洛树。在算法的这一点上，您已经完成了许多rollout，并建立了一个部分树。每个节点都跟踪了从该节点开始的任何棋盘盘面的的胜者情况。每个节点的计数都包括其所有子节点的总和。（通常，在这一点上，树会有更多的节点；在图中，我们已经为了节省空间，省略了许多节点。）

在每一轮，你添加一个新的棋盘局面到搜索树上。首先，在树的底部选择一个叶节点，在那里添加一个新的子节点。这棵树有五片叶子。为了得到最好的结果，你需要仔细选择要选哪片叶子；第4.5.2节涵盖了这样做的好策略。现在，假设你沿着最左边的树枝一直走下去。在那一点，你随机选择下一个落子，评估新的棋盘局面，并将该节点添加到树中。下图显示了经过这个过程后树的样子

树中的新节点是随机游戏的起点。你模拟游戏的其余部分，实际上只是在每个回合选择任何合法的游戏，直到游戏结束。然后你去数一数得分并找到赢家。在这种情况下，让我们假设赢家是白棋，而这是根据在新节点中的记录推出来的。此外，您还可以回到节点的所有祖先并添加他们的计数。图4.15显示了此步骤完成后树的样子。

整个过程是一轮MCTS。每当你重复一遍，树就会变大，顶部的估计就会更准确。通常情况下，你会停在一个固定的回合。在这一点上或固定的消耗时间。在这一点上，您选择的落子有最高的获胜几率。

4.5.1使用Python实现蒙特卡洛树搜索

现在您已经走完了一轮MCTS算法过程，让我们现在来看看实现的细节。首先，您将设计一个数据结构来表示MCTS树。接下来，您将编写一个函数来执行MCTS的rollout，如下面的代码所示，首先定义一个MCTS节点类，以表示树中的任何节点。每个MCTS节点类将跟踪以下属性：

• game_state--当前树中此节点的游戏状态（棋盘局面和当前玩家）。
• parent-导致这一局面的父节点。您可以将父级设置为None以指示树的根。
• move-最后一个直接导致产生这个节点的落子。
• children-树中所有子节点的列表。
• win_counts和num_rollouts-关于从这个节点开始的统计信息。
• unvisited_moves--该局面下合法但不属于树中节点的落子位置。每当向树中添加一个新节点时，就从unvisited_moves中调出一个落子位置，为它生成一个新的MCTS节点，并且将其添加到children中。

from dlgo.agent.base import Agent
from dlgo.gotypes import Point,Player

# 蒙特卡洛树节点
class MCTSNode:
    def __init__(self,game_state, Parent=None, move = None):
        # 当前节点的局面
        self.game_state = game_state
        self.Parent = Parent
        # 表示造成这个节点的上一个落子
        self.move = move
        # 展示黑白胜利的统计
        self.win_counts={
            Player.white:0,
            Player.black:0
        }
        # 表示当前的轮数
        self.num_rollouts = 0
        # 所有的子节点
        self.children = []
        # 未加入到树中节点的合法落子
        self.unvisited_move = game_state.legal_moves()

一个MCTS树节点可以通过两种方式进行修改。您可以将一个新的孩子节点添加到树中，并更新试验统计。下面的代码实现了这两个功能。

    # 随机增加一个未加入树的子节点
    def add_random_child(self):
        # 随机选一个落子
        index = random.randint(0, len(self.unvisited_moves) - 1)
        next_move = self.unvisited_moves.pop(index)
        next_state = self.game_state.apply_move(next_move)
        new_node = MCTSNode(next_state, self, next_move)
        # 将新节点加入成为该节点的子节点
        self.children.append(next_node)
        return new_node

    # 统计胜者
    def record_win(self,winner):
        self.win_counts[winner] += 1
        self.num_rollouts += 1

最后，你要添加三种方便的方法来访问树节点的有用属性：

• can_add_child表明这个局面是否还有任何尚未添加到树中的合法落子点。
• is_terminal报告游戏是否在此节点结束；如果是，则无法进一步搜索。
• winning_frac返回给定棋手在一次试验赢的概率。

    # 能否增加叶节点
    def can_add_child(self):
        return len(self.unvisited_move)>0

    # 报告游戏是否在这个节点结束
    def is_terminal(self):
        return self.game_state.is_over()

    # 该棋手当前局面赢的概率
    def winning_frac(self,player):
        return float(self.win_counts[player])/float(self.num_rollouts)

定义了树的数据结构后，现在就可以实现MCTS算法。您首先要创建一棵新树。根节点为当前棋局盘面，然后你反复进行试验。在这种实现中，您每个回合重复固定的轮数；其他的实现中运行的时间长度是固定的。

每一轮都是从沿着树走的，直到您可以在其中找到一个可以添加孩子的节点，该孩子是任何尚未加入到树中的合法落子）。select_move函数隐藏了选择最佳分支去探索的过程，我们将会在下一节中实现细节。

找到合适的节点后，调用add_random_child来选择任何后续落子并将其带到树中。此时，node是一个新创建的没有经历任何试验的MCTS节点

最后，更新新创建的节点及其所有祖先的胜者计数。整个过程实现如下

    def select_move(self,game_state):
        # 树的根节点
        root = MCTSNode(game_state)

        # 循环执行多次
        for i in range(self.num_rounds):
            node = root

            # 一直搜索到游戏在节点结束
            while (not node.can_add_child()) and (not node.is_terminal()):
                node = self.select_child(node) # 后面来实现

            # 把新的孩子节点加入到新树中.
            if node.can_add_child():
                node = node.add_random_child()

            # 从当前局面进行模拟对局，得出胜者
            winner = self.simulate_random_game(node.game_state)

            #从当前节点进行回溯更新当前及祖先胜者数
            while node is not None:
                node.record_win(winner)
                node = node.Parent

在你完成分配所有这些回合后，你需要选择一个落子点。要做到这一点，你只需循环所有顶级分支，并选择一个获胜几率最高的落子点。以下列出如何实现这一点。

 # 从根节点的诸多孩子节点中根据获胜几率选择最佳下法
        best_move = None
        win_pct = -1
        for child in root.children:
            child_pct = child.winning_frac(game_state.current_player)
            if child_pct> win_pct:
                best_move = child.move
                win_pct = child_pct
        return best_move

4.5.2 如何选择哪棵枝干去搜索

您的游戏AI在每个回合上花费的时间是有限的，这就意味着您只能执行固定数量的试验。每一次试验都提高了您对一个可能落子的评估准确度。想想看您的试验作为一个有限的资源：如果您花费额外的试验在落子A上，那么您必须花费一个较少的试验次数在落子B。你需要一个策略来决定如何分配你有限的预算。这个标准策略被称为树的上限置信区间，或UCT算法。UCT算法在两个相互冲突的目标之间取得了平衡。

第一个目标是花时间去寻找最好的落子。这个目标被称为利用（你想利用你迄今发现的任何优势）。你会把更多地试验花在具有最高估计胜率的落子点。现在，其中一些落子点有一个很高的获胜几率仅仅是偶然情况。但是当你在这些分支中完成更多的试验时，你的估计就会更准确，这种假的优势就会在列表里下降。

另一方面，如果你只试验过一个节点几次，你的估计可能会很差。纯属偶然的估计可能会使你对一个很好的落子点估计得很低。在那里多试验几次，就可能会暴露出它的真实品质。因此，你的第二个目标是为你访问最少的分支获得更准确的评估。这个目标叫做探索。

下图就比较了一棵倾向于利用的搜索树和一棵倾向于探索的树。利用与探索的权衡是试错算法的普遍特征。当我们在书的后面学到强化学习时，这个也会出现

对于您正在考虑的每个节点，您计算获胜百分比来表示利用目标。为了表示探索，您需要计算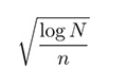，其中N是试验的总数，n是以正在考虑的节点开始的试验数量。这个具体的公式有一个理论基础；为了我们的目的，只需注意，它的价值至少是你访问过的的最大值。

将这两个组件组合起来得到UCT公式：

在这里，c是一个参数，表示您在利用和探索之间的首选平衡。UCT公式给出每个节点的分数，UCT分数最高的节点将是下一次试验的起点。 w是指你当前节点的胜率

有了更大的c值，您将花费更多的时间去试验访问次数最少的节点。使用较小的c值，您将花费更多的时间收集对更好评估的节点。c大小的选择会影响游戏玩家的有效性，这通常是通过试错找到的。我们建议从1.5左右开始，然后从那里进行实验。参数c有时被称为temperature。当温度“更热”时，你的搜索会更不稳定，当温度“更冷”时，你的搜索会更集中。

下面代码展示了如何实现此策略。在确定要使用的度量方法之后，选择一个子节点将是一个简单的问题，即计算每个节点的UCT值并选择最大UCT值的节点。就像在极小极大搜索中一样，你需要在每个回合上来回去切换你的视角。你需要从下一个落子的棋手角度去计算获胜几率，当你沿着树搜索时，视角就会在黑棋和白棋之间进行切换。

  # 计算UCT分值
  def get_UCT_score(child_rollout, parent_rollout, win_prc, temperature):
    exploration = math.sqrt(math.log(parent_rollout)/child_rollout)
    return win_prc + temperaature*exploration


  # 选择最佳孩子节点(即UCT分数最高）
    def select_child(self,node):
        # 获得其孩子节点试验的总数,即为父节点的试验次数
        total_rollouts = sum(child.num_rollouts for child in node.children)

        # 遍历该节点的孩子节点，获得最佳分数的孩子
        best_score = -1
        best_child = None
        for child in node.children:
            # 获得该孩子节点的UCT分数
            score = get_UCT_score(child.num_rollouts, total_rollouts, child.winning_frac(node.game_state.current_player),self.temperature )
            if score > best_score:
                best_score = score
                best_child = child
        return  best_child

4.5.3 应用蒙特卡洛树搜索到围棋中

在上一节中，您实现了MCTS算法的一般形式。直截了当的MCTS实现的围棋AI可以达到业余1段左右的水平，这是一个强大的业余玩家的水平。将MCTS与其他技术结合将可以产生一个比这更强的AI；今天的许多顶级围棋AI都使用MCTS和深度学习。如果你有兴趣与您的MCTS AI进行对弈，本节将涵盖一些实际的细节。

MCTS算法在19路围棋中将开始成为一种可行的战略，每回合将达到10,000轮试验。本章中的实现速度不够快，无法做到这一点：每一步你将等待几分钟，因此你将需要进行优化，以便在合理的时间内完成许多试验。另一方面，在小棋盘上，甚至你的参照实现也会产生一个有趣的对手。

在所有其他相同的情况下，更多的试验意味着一个更好的决定。只要加快代码速度，就可以使你的机器人变得更强大，从而在同样的时间内做出更多的试验。这不是MCTS特定的代码，而是相关的代码。例如，计算吃子的代码在每次试验要进行数百次。所有的基本游戏逻辑都是公平的优化游戏。

随机试验期间选择落子的算法称为试验策略。你的试验政策越真实，你的评估就越准确。在第三章中，你实现了一个随机落子AI，您可以使用这个随机落子AI作为您的试验策略。但是随机落子AI在没有围棋知识的情况下完全随机地选择落子是不完全正确。首先，在棋盘不满的时候，你的程序不会pass或投降。第二，你编程它不是为了填满它自己的眼睛，所以它不会在游戏结束时杀死自己的石头。没有这种逻辑，试验将不太准确。

一些MCTS的实现更进一步，并在其试验策略中实现了更多的围棋特定逻辑。带有特定游戏逻辑的试验有时被称为重试验；相比之下，接近纯粹随机的试验有时被称为轻试验。实现重试验的一种方法是建立一个基本的常见的棋形列表，以及一个已知的应对。在围棋盘上找到任何的已知形状，您就可以查找到已知的应对方法并提高其被选中的概率。你不想总是把已知的应对方法作为一条硬性的、快速的规则来选择，因此你将会从算法中随机删除重要的元素。

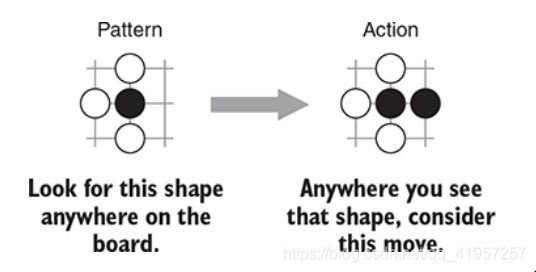
一个例子如下图所示..这是一个3×3的局部模式，其中一个黑棋有可能在白棋在下一回合被吃掉。黑棋可以通过逃跑暂时存活。这个并不总是最好的落子；它甚至不总是一个好的落子，但总比棋盘上进行随机落子要好

建立一个好的这些模式需要一些围棋战术的知识。如果您对其他战术模式感到好奇，您可以在大量试验中使用这些模式，我们建议查看Fuego（http://fuego.sourceforge.net/）或Pachi（https://github.com/pasky/pachi），两个开源MCTS 围棋引擎的源码。

在实施重试验时要仔细。如果您的试验策略中的逻辑计算缓慢，则不能执行那么多的试验。你可能会被那些拥有更复杂逻辑的AI所击败。

制作一个游戏AI不仅仅是开发算法的最佳练习，这也是为了给人类对手创造一个有趣的体验。其中一部分乐趣来自于让人类玩家有胜利的满足感。你在这本书中实现的第一个围棋机器人，RandomAgent，正在进行疯狂地对抗。在人类玩家不可避免地要赢棋之后，随机机器人却要一直坚持到棋盘全部占满。无法阻止人类获胜，如果能让你的AI可以投降的话将会是一种更好的体验。

除了基本的MCTS实现之外，您还可以轻松地添加人性化的投降逻辑。在选择落子的过程中，MCTS算法计算一个估计的获胜百分比。在一轮中，你比较这些数字来决定要选择什么落子。但你也可以比较同一游戏中不同点的估计获胜百分比。如果这些数字在下降，说明人类取得了优势。当最佳选项的获胜百分比足够低时，比如10%，你就可以让你的机器人投降。

4.6 总结

当你没有一个好的局面评估函数，你有时可以使用蒙特卡罗树搜索。该算法从特定局面开始模拟随机游戏，并跟踪哪个棋手获胜更多。

经过试验，在5*5的棋盘上如果使用原来的RandomBot()进行模拟500次试验，非常慢，因此换成了之前用佐布里斯特散列做出的随机落子AI，在5*5的棋盘上进行500次模拟只需10秒多，如下图

我们加入一些代码显示AI模拟对局时的胜率（放在select_move里）

 scored_moves = [
            (child.winning_frac(game_state.current_player), child.move, child.num_rollouts)
            for child in root.children
        ]
        scored_moves.sort(key=lambda x: x[0], reverse=True)
        for s, m, n in scored_moves[::]:
            print('%s - %.3f (%d)' % (m, s, n))

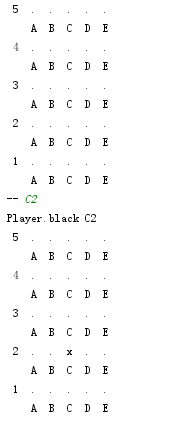
结果：我下在C2

AI经过模拟发现（5,4）胜率最高，于是就选择了（5,4），其中括号内的数字代表该下法的试验次数

当我把试验次数调到5000次，棋盘大小改为7*7,且temperature大小改为1,同时我把黑的贴目改为3时，其棋力已经有了进步，如下图

黑棋下在E3,白棋经过5000盘模拟之后，准确地下在D2

 不过AI每下一步棋就要花上4分钟左右的时间，这要是19*19，那时间可能一小时都顶不住，大家可以根据情况调整模拟次数和temperature