K-Means聚类与DBSCAN聚类-手写实现

K-Means聚类与DBSCAN聚类-手写实现

近来学习聚类算法，了解了两种类型的聚类方法的原理，然后兴致勃勃想自行写代码实现一波。
原理都还挺好理解的，写代码总体来说也还轻松，如果有哪里不对的地方欢迎在评论下方指正或私聊我，共同进步哈

---

---

1 原理介绍

1.1 K-means聚类

K-Means可以说是最基本的一种无监督聚类算法，应该大家接触聚类的第一个算法都是kmeans。

K-Means的原理应该比较简单，网上也有挺多对于模型推导的文章，大家可以自行查阅。一句话概括起来，就是通过不断更新迭代中心点，找到合适的类别中心。

K-Means方法的应用是很广的，因为其简单、易于理解的几个特性。但同时，kmeans方法也是不稳定的，意思是其聚类的效果有时候是不同的，可能有些情况这些点聚成一类，另一些情况则不是，受到初始聚类中心的选择的影响。同时类别的个数k事先也是不太好确定的，当然如果不怕耽误时间可以让k从2一直递增的重复实验，直到找到一个满意的k。

1.2 DBSCAN聚类

我们知道，我们常见的距离的度量（距离的度量在聚类过程中非常核心）通常是欧式距离或者是曼哈顿距离，这样距离的特点是，通常聚类出来的结果是一个凸集，这里不强调凸集的数学定义，直观的理解就是类别的边界都是往外凸的。那如果遇到类别的集合并非凸集的情况，比如两个相对的圆环（可见下面的示例），传统的kmeans就显得无能为力了。

此时这里介绍一种DBSCAN的聚类方法(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)。DBSCAN是一种典型的基于密度的聚类方法，可以适用于凸集和非凸集。为了便于对后面代码的理解，建议先行了解这种聚类方法中的几个关于密度的概念。下面做一些简单的阐释。

用来描述密度有两个重要的参数，一个是$\epsilon$，表示邻域的直径（回想起高数第一章邻域的知识点么），另一个是$min\_points$在以$\epsilon$为直径内的样本点的数量。直观的理解就是在一个$\epsilon$大的圈里面有多少个点，如果$\epsilon$越小，而$min\_points$越大，说明密度越大。

• 核心对象
  以一个点为中心的$\epsilon$邻域内存在多于$min\_points$的对象，则该点为核心对象
• 密度直达
  以$x_i$为中心的邻域内其它任意点$x_j$，称$x_j$由$x_i$密度直达（注意反过来不一定成立，除非$x_j$也是核心对象哦），记为$x_i\Rightarrow x_j$
• 密度可达
  说白了就是密度直达使用了一下传递规律。三个点$x_i$、$x_j$、$x_k$，满足下面的关系：$x_i\Rightarrow x_j$，$x_j\Rightarrow x_k$，那么可以推出$x_i\to x_k$，其中“$\to$”这个箭头表示密度可达
• 密度相连
  对于$x_i$、$x_j$，存在一个核心对象$x_k$使得$x_k\to x_i$、$x_k\to x_j$成立，称$x_i$、$x_j$密度相连。体会密度相连和密度可达的的区别，密度相连是针对任意两个点的，而密度可达是类似于找到两个点之间密度直达的相连关系。

而DBSCAN的聚类的核心思想就是：通过密度可达关系导出的所有密度相连对象所组成的簇

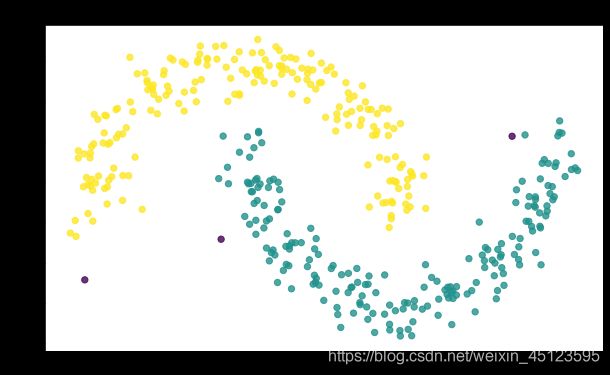
为了方便大家理解这些概念，用下面的示意图进行简单的表示：

黄色的点是核心对象，紫色的点不是核心对象。然后这些连成一片的黄色的点以及在红色圈之内的紫色的点是互相密度相连的（密度相连是DBSCAN的核心和代码的关键）

而关于算法的流程，这里就不再详细讲了，参考下面的代码即可

---

2 KMeans实现

2.1 导入相关库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

2.2 定义一些方法

def make_data(n_samples=200, centers=4, n_features=2, cluster_std=2.5, random_state=42):
	"""制造数据"""
    return make_blobs(n_samples=n_samples, 
    				centers=centers, 
    				n_features=n_features, 
    				cluster_std=cluster_std, 
    				random_state=random_state)

def distance(x, c):
    """计算距离，这里用的欧式距离"""
    return np.linalg.norm(np.array(x) - center.get(c))

def update_cluster(x):
	"""判定类别，x指的是点到各个样本中心的距离"""
    return np.argmin(x.values)+1

def update_center(center):
	"""更新类别中心"""
    new_center = {
     }
    for c in center.keys():
        if len(df[df.cluster == int(c)]) == 0:
            new_center[c] = center[c]
        else:
            new_center[c] = df[df.cluster == int(c)][['x1','x2']].mean().values
    return new_center

def check_dict_equal(d1, d2):
	"""判断两个中心坐标字典是否相等，这里主要比较值是否一样"""
    for k, v1 in d1.items():
        v2 = d2.get(k)
        if np.abs(v2 - v1).all() > 0.01:
            return False
    return True

2.3 代码逻辑及示例

## 准备数据
x, y = make_data(n_samples=600)

## 定义一些参数
k = 4 ## 指定类别数量
max_iter = 50 ## 指定最大的循环次数

## 处理数据
# 主要用pandas处理，df的apply方法真香！！！
df = pd.DataFrame(x,columns=['x1','x2']) 
# 生成k个初始点
x1_min, x1_max = df['x1'].min(), df['x1'].max()
x2_min, x2_max = df['x2'].min(), df['x2'].max()
start_x1 = x1_min + np.random.rand(k) * (x1_max- x1_min)
start_x2 = x2_min + np.random.rand(k) * (x2_max- x2_min)
center = {
     }
for i in range(k):
	# 中心点随机生成，保存在center
    center[f"{i+1}"] = np.array([start_x1[i], start_x2[i]])
    df[f"{i+1}"] = 0

df['cluster'] = 0 # 初始化类别中心为0

for epoch in range(max_iter):
    ##计算距离
    for c in center.keys():
        df[c] = df[['x1','x2']].apply(lambda x: distance(x,c), axis=1)
    ## 确定类别
    df['cluster'] = df[list(center.keys())].apply(lambda x: update_cluster(x), axis=1)
    ## 获取新的类别中心
    new_center = update_center(center)
    ## 判断两个中心是否一致或者差距足够小
    flag = check_dict_equal(center, new_center)
    if flag: # 两次迭代的中心点基本没变化，直接退出迭代
        break
    else:
        center = new_center

2.4 结果与分析

关于性能方面我就不多讲了，有兴趣的小伙伴可以去试试，我直观的感受是，比sklearn中的模型训练速度相差…很大

好了，下面主要展示一些结果
原始生成的的数据是：

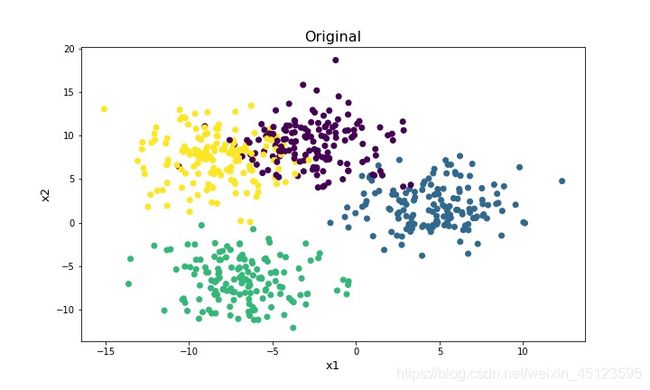
可以看到这个数据也不是特别标准的，有些即使是人去分也很难区分的，下面是用自己写的kmeans代码跑的结果（为了让大家更加直观的看到迭代过程，我制作了一个gif）

再看另一次训练的

用sklearn中的包训练同样的数据

## 使用sklearn中的包进行建模
km = KMeans(n_clusters=4)
km.fit(df[['x1','x2']].values)
predict_y = km.predict(df[['x1','x2']].values)

讲真的，只有自己手写过代码才知道这个包这么好用，短短的三行代码，简洁方便还很快

输出的结果

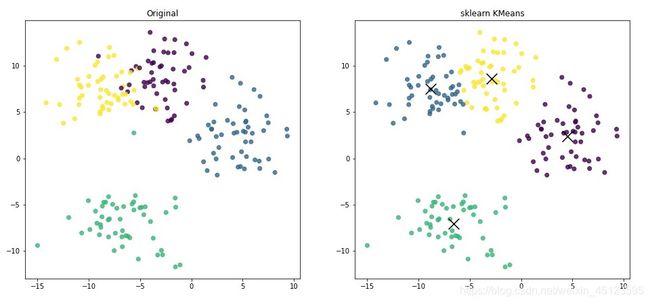
可以看到跟我们的结果是一样的，然后对比了一下自己代码的几个中心点的坐标，跟sklearn包训练的结果是基本一样的

kmeans在非凸集下的表现

为了引出下面的方法，用kmeans在非凸集上面进行了一些训练

下面是分两个类别，$k=2$

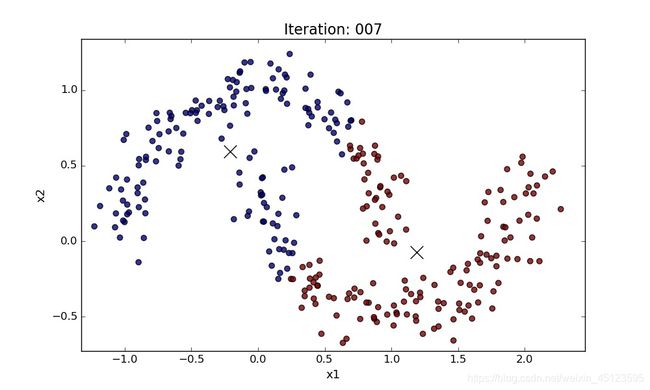
那如果把k调的比较大呢，比如$k=9$

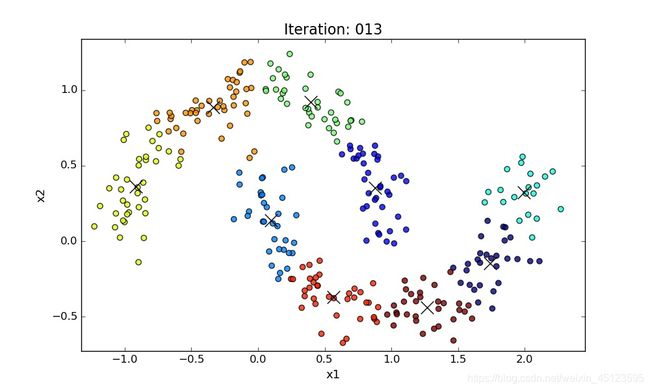
可以看到如果k比较小的话，是不可能分出这些类别来的；但是k如果比较大的话，仔细看还是可以看到，两个类别是可以被分开的，只不过这两个类分别又被分割成了若干个小的类。但我们觉得这样是远远不够的，如果说有很多个属性呢，那么对于可视化就成了难题了，怎么去把这些小的类合并成我们想要的那个类呢，所以下面要介绍DBSCAN的方法

---

3 DBSCAN实现

3.1 算法与代码

先定义一些方法

def distance2(x1, x2):
	"""计算距离，这里还是用的欧式距离"""
    return np.linalg.norm(np.array(x1) - np.array(x2))

def is_core(df, x, index, imi, min_points):
    """判断是否是核心对象"""
    new_df = pd.DataFrame()
    ## 在原有df的基础上限定范围，减少计算量
    t = df.loc[index, ['x1','x2']].values
    x_1, x_2 = t[0], t[1]
    x1_min, x1_max, x2_min, x2_max = x_1-imi, x_1+imi, x_2-imi, x_2+imi
    df1 = df[(df.x1>x1_min) & (df.x1<x1_max) & (df.x2>x2_min) & (df.x2<x2_max)]
    new_df['distance'] = df1[['x1','x2']].apply(lambda x1: distance2(x1, x), axis=1)
    temp_df = new_df[new_df.distance <= imi]
    if len(temp_df) >= min_points:
        # 此时temp_df里面的点是该点邻域范围内的所有点，将其保存一下
        next_index = temp_df.index
        v = " ".join([str(i) for i in next_index])
        df.loc[index, 'next'] = v
        return 1
    return 0

## 密度聚类
def dbscan_cluster(df):
    df['cluster'] = 0 # 初始化所有点的类别，未被分类或者无法分类的离散点标记为0
    c_df = df[df.is_core==1]
    label = 0
    # 当还有核心对象且核心对象未被归类
    while len(c_df[c_df.cluster==0])>0 and label<len(df): 
        label += 1
        # 顺序找到第一个核心对象且类别为0的样本点
        c_df = df[df.is_core==1]
        if len(c_df[c_df.cluster==0])>0:
            c_index = c_df[c_df.cluster==0].index[0] # 核心点的index
            # 当前这个点邻域内的点，密度相连
            now_set = set([int(i) for i in df.loc[c_index, 'next'].split(" ")])
            ## 接下来找以这个点为中心的密度相连的其它点
            while len(now_set) > 0:
                # 拿出其中的一个元素
                element = list(now_set)[0]
                now_set.remove(element)
                # 判断这个点是否已经判断过了，如果已经有实际意义的标签则不需要再加入其邻域的点了
                if df.loc[element, 'cluster'] == 0: # 没有判断过
                    # 如果该元素是核心对象，则将其邻域的点加入到now_set
                    if df.loc[element, 'is_core'] != 0:
                        now_set  = now_set | set([int(i) for i in df.loc[element, 'next'].split(" ")])
                    # 将索引为element的点的类别标签置为label
                    df.loc[element, 'cluster'] = label
    return df

算法的逻辑

## 数据
x, y = make_moons(n_samples=400, noise=0.1, random_state=42)

## 参数
imi = 0.22 # 邻域半径
min_points = 4 # 最少的点数

## 获取核心对象以及核心对象的邻域点
df = pd.DataFrame(x,columns=['x1','x2'])
df['is_core'] = 0 # 是否是核心对象
df['next'] = "" # 若是核心对象，则其邻域点的index，如果不是核心对象，则值为""
for i in range(len(df)): # 找到所有核心对象
    x = df.iloc[i][['x1','x2']].values
    df.loc[i, 'is_core'] = is_core(df, x, i, imi, min_points)

## 使用DBSCAN的方法寻找密度相连的点集，并基于此分类
df = dbscan_cluster(df) # 这一步可以往前看方法的过程

3.2 结果展示与分析

下面是上面代码跑的结果

参数对于DBSCAN的影响

上面用的参数是：$\epsilon =0.2，min\_points=4$，下面看看不同参数下情况如何（参数可见图上面的标题）



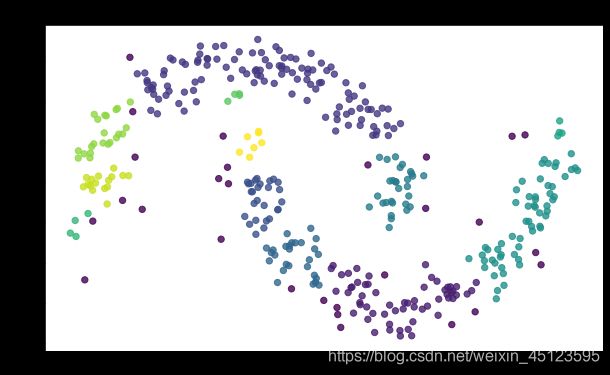
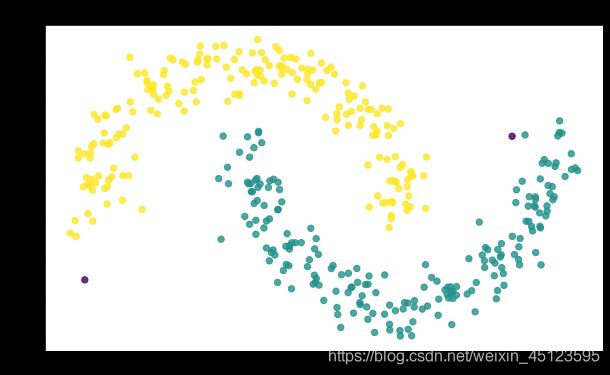
可以看到如果参数设置不当会造成结果出现比较大的波动，有时候分不开不同的类，有时候分的太多类了；不同的参数选择有时候可以达到同样的分类效果。这也可以看做是DBSCAN的一个缺陷，面对未知问题的时候，我们也不太清楚怎么去设置$\epsilon 、min\_points$两个参数，只能通过经验以及反复的尝试。

---

总结

上面介绍了两种聚类的方法，供大家学习和参考。两种聚类的方式都有各自使用的场景，也欢迎大家在评论区分享自己的使用经验。文章原创不易，欢迎点赞收藏转发和打赏