强连通图的算法
有向图强连通分量的Tarjan算法 [有向图强连通分量]
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
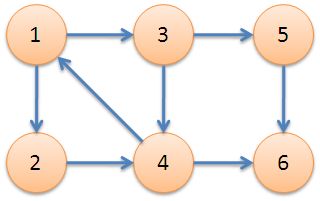
直接根据定义,用双向遍历取交集的方法求强连通分量,时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法,两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。 [Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出,
Low(u)=Min
{
DFN(u),
Low(v),(u,v)为树枝边,u为v的父节点
DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)
}
当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下
- tarjan<SPAN style="COLOR: #66cc66">(</SPAN>u<SPAN style="COLOR: #66cc66">)</SPAN>
- <SPAN style="COLOR: #66cc66">{</SPAN>
- DFN<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN>=Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN>=++Index <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 为节点u设定次序编号和Low初值</SPAN>
- Stack.<SPAN style="COLOR: #202020">push</SPAN><SPAN style="COLOR: #66cc66">(</SPAN>u<SPAN style="COLOR: #66cc66">)</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 将节点u压入栈中</SPAN>
- <SPAN style="COLOR: #b1b100">for</SPAN> each <SPAN style="COLOR: #66cc66">(</SPAN>u, v<SPAN style="COLOR: #66cc66">)</SPAN> in E <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 枚举每一条边</SPAN>
- <SPAN style="COLOR: #b1b100">if</SPAN> <SPAN style="COLOR: #66cc66">(</SPAN>v is not visted<SPAN style="COLOR: #66cc66">)</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 如果节点v未被访问过</SPAN>
- tarjan<SPAN style="COLOR: #66cc66">(</SPAN>v<SPAN style="COLOR: #66cc66">)</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 继续向下找</SPAN>
- Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN> = min<SPAN style="COLOR: #66cc66">(</SPAN>Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN>, Low<SPAN style="COLOR: #66cc66">[</SPAN>v<SPAN style="COLOR: #66cc66">]</SPAN><SPAN style="COLOR: #66cc66">)</SPAN>
- <SPAN style="COLOR: #b1b100">else</SPAN> <SPAN style="COLOR: #b1b100">if</SPAN> <SPAN style="COLOR: #66cc66">(</SPAN>v in S<SPAN style="COLOR: #66cc66">)</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 如果节点v还在栈内</SPAN>
- Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN> = min<SPAN style="COLOR: #66cc66">(</SPAN>Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN>, DFN<SPAN style="COLOR: #66cc66">[</SPAN>v<SPAN style="COLOR: #66cc66">]</SPAN><SPAN style="COLOR: #66cc66">)</SPAN>
- <SPAN style="COLOR: #b1b100">if</SPAN> <SPAN style="COLOR: #66cc66">(</SPAN>DFN<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN> == Low<SPAN style="COLOR: #66cc66">[</SPAN>u<SPAN style="COLOR: #66cc66">]</SPAN><SPAN style="COLOR: #66cc66">)</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 如果节点u是强连通分量的根</SPAN>
- repeat
- v = S.<SPAN style="COLOR: #202020">pop</SPAN> <SPAN style="FONT-STYLE: italic; COLOR: #808080">// 将v退栈,为该强连通分量中一个顶点</SPAN>
- print v
- until <SPAN style="COLOR: #66cc66">(</SPAN>u== v<SPAN style="COLOR: #66cc66">)</SPAN>
- <SPAN style="COLOR: #66cc66">}</SPAN>
tarjan(u) { DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值 Stack.push(u) // 将节点u压入栈中 for each (u, v) in E // 枚举每一条边 if (v is not visted) // 如果节点v未被访问过 tarjan(v) // 继续向下找 Low[u] = min(Low[u], Low[v]) else if (v in S) // 如果节点v还在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根 repeat v = S.pop // 将v退栈,为该强连通分量中一个顶点 print v until (u== v) }
接下来是对算法流程的演示。
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
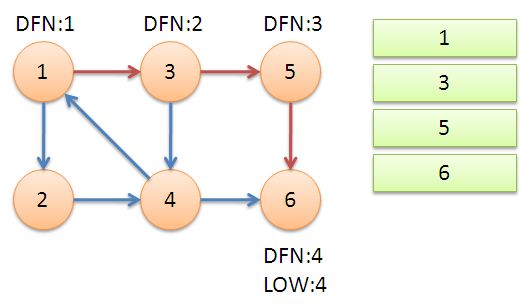
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
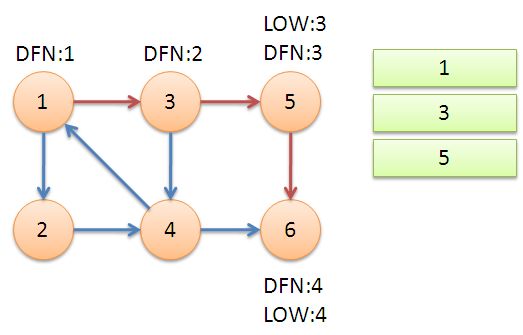
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
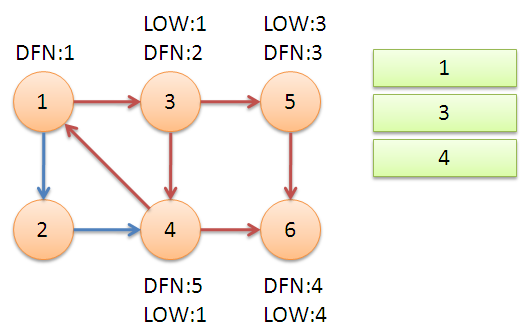
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
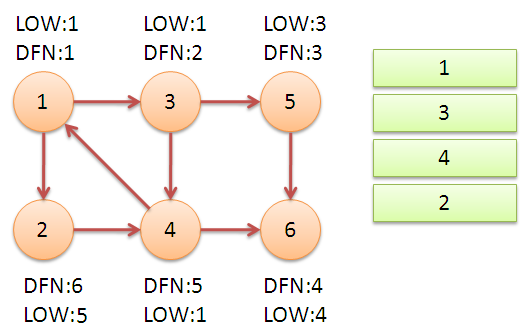
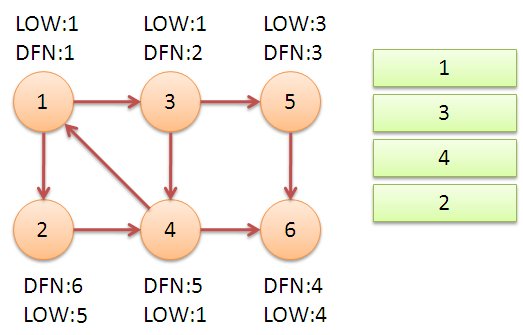
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
求有向图的强连通分量还有一个强有力的算法,为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法,其时间复杂度也是 O(N+M)。与Trajan算法相比,Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS,不用建立逆图,更简洁。在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外,该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法,也有助于深入理解求双连通分量的Tarjan算法,两者可以类比、组合理解。
求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法,以及求最近公共祖先的离线Tarjan算法,在此对Tarjan表示崇高的敬意。
附:tarjan算法的C++程序
[c] view plaincopyprint?
01. <PRE class=cpp name="code">#include<iostream>
02.#include<cstring>
03.#include<cstdio>
04.using namespace std;
05.#define N 100
06.#define M 100
07.struct Edge
08.{
09. int v;
10. int next;
11.};
12.Edge edge[M];//边的集合
13.
14.int node[N];//顶点集合
15.int instack[N];//标记是否在stack中
16.int stack[N];
17.int Belong[N];//各顶点属于哪个强连通分量
18.int DFN[N];//节点u搜索的序号(时间戳)
19.int LOW[N];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
20.int n, m;//n:点的个数;m:边的条数
21.int cnt_edge;//边的计数器
22.int Index;//序号(时间戳)
23.int top;
24.int Bcnt;//有多少个强连通分量
25.
26.void add_edge(int u, int v)//邻接表存储
27.{
28. edge[cnt_edge].next = node[u];
29. edge[cnt_edge].v = v;
30. node[u] = cnt_edge++;
31.}
32.void tarjan(int u)
33.{
34. int i,j;
35. int v;
36. DFN[u]=LOW[u]=++Index;
37. instack[u]=true;
38. stack[++top]=u;
39. for (i = node[u]; i != -1; i = edge[i].next)
40. {
41. v=edge[i].v;
42. if (!DFN[v])//如果点v没被访问
43. {
44. tarjan(v);
45. if (LOW[v]<LOW[u])
46. LOW[u]=LOW[v];
47. }
48. else//如果点v已经被访问过
49. if (instack[v] && DFN[v]<LOW[u])
50. LOW[u]=DFN[v];
51. }
52. if (DFN[u]==LOW[u])
53. {
54. Bcnt++;
55. do
56. {
57. j=stack[top--];
58. instack[j]=false;
59. Belong[j]=Bcnt;
60. }
61. while (j!=u);
62. }
63.}
64.void solve()
65.{
66. int i;
67. top=Bcnt=Index=0;
68. memset(DFN,0,sizeof(DFN));
69. memset(LOW,0,sizeof(LOW));
70. for (i=1;i<=n;i++)
71. if (!DFN[i])
72. tarjan(i);
73.}
74.int main()
75.{
76. freopen("in.txt","r",stdin);
77. int i,j,k;
78. cnt_edge=0;
79. memset(node,-1,sizeof(node));
80. scanf("%d%d",&n,&m);
81. for(i=1;i<=m;i++)
82. {
83. scanf("%d%d",&j,&k);
84. add_edge(j,k);
85. }
86. solve();
87. for(i=1;i<=n;i++)
88. printf("%d ",Belong[i]);
89.}
90.
91.</PRE><BR>