一、应用场景:地图应用中判断一个位置是否在一个区域内。我曾经应用在百度地图上,代码为js实现。据我了解,目前百度地图api已经提供该功能。
二、概要:
1、行政区划边界是多边形;
2、多边形分为凸多边形和凹多边形;
3、应用:产生随机数据(即一个平面坐标)在制定的行政区划边界以内(即多边形内),在正式情况下不需要从图形的层面处理数据,数据本身就有在那个区划下的属性。
三、假定:
1、多边形的点都是不重合的点;
2、给定的多边形边界坐标集就是时针顺序的,即要么符合逆时针顺序要么符合顺时针顺序,不存在这种情况:
第一个点是时钟上1的位置,第二个点是时钟上3的位置,第三个点回到1和3之间的位置,如2.如果多边形上包含2的位置,那么给点的坐标集应该是1、2、3,而不应该是1、3、2.
四、原理:
1、对于凸多边形来说,一个点与多边形边界所有连续的两点构成的夹角的和为360度,则说明该点在多边形内。如果夹角和不是360度,则该点一定不在多边形内。
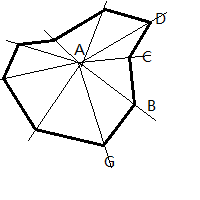 如图,A与多边形上的点构成的夹角是360°说明A在多边形内。
如图,A与多边形上的点构成的夹角是360°说明A在多边形内。
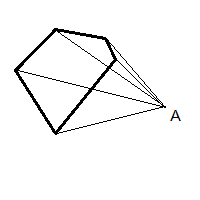 如图,点A与多边形上的点构成的夹角不是360°,说明A不在多边形内。
2、对于凹多边形来说,将凹的部分可能重复计算夹角的地方调整坐标在集合中的顺序后计算夹角。
如图,点A与多边形上的点构成的夹角不是360°,说明A不在多边形内。
2、对于凹多边形来说,将凹的部分可能重复计算夹角的地方调整坐标在集合中的顺序后计算夹角。
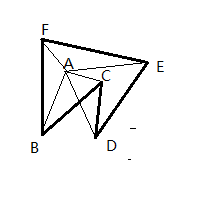 在按照原理1会计算∠BAC加上∠CAD的值,如图,实际上∠CAD是是∠BAC的一部分,所以这里要么累加时不要包含∠CAD的值;要么调整CD两点的位置,利用原理1,计算∠BAD加上∠DAC(调整位置后就是∠CAD)。问题是,什么时候需要调整CD的位置,我们发现在原理1中,在多边形内的点与多边形上的点的连线与多边形边界没有交点,而该图有交点。
所以若第一个点A与地图上出去BC两点的任意一点D的连线,若与BC两点的连线存在交点,那么这是需要调整任意一点D与B的位置(或C的位置)。这个过程是对坐标集排序的过程。之后利用原理1即可。
五、代码实现(javascript):
我的博客园相关代码访问地址: http://www.cnblogs.com/langu/p/3458846.html
http://www.cnblogs.com/langu/p/3458835.html
1、两个点间的距离
获取坐标轴内两个点间的距离
function getLength(point1_x, point1_y, point2_x, point2_y)
{
var diff_x = Math.abs(point2_x - point1_x);
var diff_y = Math.abs(point2_y - point1_y);
var length_pow = Math.pow(diff_x, 2) + Math.pow(diff_y, 2);//两个点在 横纵坐标的差值与两点间的直线 构成直角三角形。length_pow等于该距离的平方
return Math.sqrt(length_pow);
}
2、获得三个点构成的三角形的 第一个点所在的角度的余弦值
function getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y)
{
var length1_2 = getLength(point1_x, point1_y, point2_x, point2_y);//获取第一个点与第2个点的距离
var length1_3 = getLength(point1_x, point1_y, point3_x, point3_y);
var length2_3 = getLength(point2_x, point2_y, point3_x, point3_y);
var res = (Math.pow(length1_2, 2) + Math.pow(length1_3, 2) - Math.pow(length2_3, 2)) / (length1_2 * length1_3 * 2);//cosA=(pow(b,2)+pow(c,2)-pow(a,2))/2*b*c
return res;
}
var pi180 = 180 / Math.PI;
3、将余弦值转换为角度
//获取3个点的夹角,角顶点为第一个点
function getAngle(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y)
{
var _cos1 = getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y);//第一个点为顶点的角的角度的余弦值
return Math.acos(_cos1) * pi180;
}
4、已知4个点的坐标,求两个线段的交点坐标。对应原理2中的ABCD四个点。
//判断第一个点 与 第四个点所连直线 与 第2个点和第3个点 所连直线的交点 是否在 第2个和第3个点的线段上
function getCrossPoint(point1, point2, point3, point4)
{
var pD_x = point1.split(',')[0];
var pD_y = point1.split(',')[1];
var pA_x = point2.split(',')[0];
var pA_y = point2.split(',')[1];
var pC_x = point3.split(',')[0];
var pC_y = point3.split(',')[1];
var pB_x = point4.split(',')[0];
var pB_y = point4.split(',')[1];
var k_y = (pB_x * pC_y * pD_y - pD_x * pB_y * pC_y - pA_y * pB_x * pD_y + pD_x * pB_y * pA_y + pC_x * pA_y * pD_y - pA_x * pC_y * pD_y - pC_x * pB_y * pA_y + pA_x * pB_y * pC_y) /
(pD_y * pC_x - pA_x * pD_y - pB_y * pC_x + pA_x * pB_y + pB_x * pC_y - pD_x * pC_y - pA_y * pB_x + pA_y * pD_x);
var k_x = (pD_y * (pC_x - pA_x) * (pB_x - pD_x) - pA_y * (pC_x - pA_x) * (pB_x - pD_x) + pA_x * (pC_y - pA_y) * (pB_x - pD_x) + pD_x * (pD_y - pB_y) * (pC_x - pA_x)) /
((pC_y - pA_y) * (pB_x - pD_x) + (pD_y - pB_y) * (pC_x - pA_x));
return k_x + ',' + k_y;
}
5、两条线的交点,不一定在线段上,有可能在线段的延长线上,所以需要判断交点是否在线段上
//判断 随机产生的点 和点X 的连线 与地图上已知的两点(给出的坐标中连续的两点)之间的连线 的 交点 是否在 已知的两点的线段之上 如果在之上:那么点X的顺序应该调整到已知的两点中间
function CrosspointIsOnTheLine(point1, point2, point3, point4)
{
var crossPoint = getCrossPoint(point1, point2, point3, point4);//交点坐标
var result = {
online: false,//是否在线段上
nearP2: undefined//如果不在线段上,是否近p2,否则近p3
};
//交点分别到 第2点 和 第3点 之间的距离 等于 第2点到第3点的距离 那么 交点在线段上
var cp_xy = crossPoint.split(',');
var p2_xy = point2.split(',');
var p3_xy = point3.split(',');
var cp_p2_length = getLength(cp_xy[0], cp_xy[1], p2_xy[0], p2_xy[1]);//交点到p2的距离
var cp_p3_length = getLength(cp_xy[0], cp_xy[1], p3_xy[0], p3_xy[1]);//交点到p3的距离
var p2_p3_length = getLength(p2_xy[0], p2_xy[1], p3_xy[0], p3_xy[1]);//p2到p3的距离
//由于线段的长度本身存在精度的问题 ,所以这么比较 交点到 p2和p3的距离 同时小于 p2到p3的距离 说明 交点在 p2到p3的线段上
if (cp_p2_length <= p2_p3_length && cp_p3_length <= p2_p3_length) {
result.online = true;
}
else {
//if (cp_p2_length > p2_p3_length) {
// result.nearP2 = false;
//}
//else if (cp_p3_length > p2_p3_length) {
// result.nearP2 = true;
//}
}
return result;
}
在按照原理1会计算∠BAC加上∠CAD的值,如图,实际上∠CAD是是∠BAC的一部分,所以这里要么累加时不要包含∠CAD的值;要么调整CD两点的位置,利用原理1,计算∠BAD加上∠DAC(调整位置后就是∠CAD)。问题是,什么时候需要调整CD的位置,我们发现在原理1中,在多边形内的点与多边形上的点的连线与多边形边界没有交点,而该图有交点。
所以若第一个点A与地图上出去BC两点的任意一点D的连线,若与BC两点的连线存在交点,那么这是需要调整任意一点D与B的位置(或C的位置)。这个过程是对坐标集排序的过程。之后利用原理1即可。
五、代码实现(javascript):
我的博客园相关代码访问地址: http://www.cnblogs.com/langu/p/3458846.html
http://www.cnblogs.com/langu/p/3458835.html
1、两个点间的距离
获取坐标轴内两个点间的距离
function getLength(point1_x, point1_y, point2_x, point2_y)
{
var diff_x = Math.abs(point2_x - point1_x);
var diff_y = Math.abs(point2_y - point1_y);
var length_pow = Math.pow(diff_x, 2) + Math.pow(diff_y, 2);//两个点在 横纵坐标的差值与两点间的直线 构成直角三角形。length_pow等于该距离的平方
return Math.sqrt(length_pow);
}
2、获得三个点构成的三角形的 第一个点所在的角度的余弦值
function getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y)
{
var length1_2 = getLength(point1_x, point1_y, point2_x, point2_y);//获取第一个点与第2个点的距离
var length1_3 = getLength(point1_x, point1_y, point3_x, point3_y);
var length2_3 = getLength(point2_x, point2_y, point3_x, point3_y);
var res = (Math.pow(length1_2, 2) + Math.pow(length1_3, 2) - Math.pow(length2_3, 2)) / (length1_2 * length1_3 * 2);//cosA=(pow(b,2)+pow(c,2)-pow(a,2))/2*b*c
return res;
}
var pi180 = 180 / Math.PI;
3、将余弦值转换为角度
//获取3个点的夹角,角顶点为第一个点
function getAngle(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y)
{
var _cos1 = getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y);//第一个点为顶点的角的角度的余弦值
return Math.acos(_cos1) * pi180;
}
4、已知4个点的坐标,求两个线段的交点坐标。对应原理2中的ABCD四个点。
//判断第一个点 与 第四个点所连直线 与 第2个点和第3个点 所连直线的交点 是否在 第2个和第3个点的线段上
function getCrossPoint(point1, point2, point3, point4)
{
var pD_x = point1.split(',')[0];
var pD_y = point1.split(',')[1];
var pA_x = point2.split(',')[0];
var pA_y = point2.split(',')[1];
var pC_x = point3.split(',')[0];
var pC_y = point3.split(',')[1];
var pB_x = point4.split(',')[0];
var pB_y = point4.split(',')[1];
var k_y = (pB_x * pC_y * pD_y - pD_x * pB_y * pC_y - pA_y * pB_x * pD_y + pD_x * pB_y * pA_y + pC_x * pA_y * pD_y - pA_x * pC_y * pD_y - pC_x * pB_y * pA_y + pA_x * pB_y * pC_y) /
(pD_y * pC_x - pA_x * pD_y - pB_y * pC_x + pA_x * pB_y + pB_x * pC_y - pD_x * pC_y - pA_y * pB_x + pA_y * pD_x);
var k_x = (pD_y * (pC_x - pA_x) * (pB_x - pD_x) - pA_y * (pC_x - pA_x) * (pB_x - pD_x) + pA_x * (pC_y - pA_y) * (pB_x - pD_x) + pD_x * (pD_y - pB_y) * (pC_x - pA_x)) /
((pC_y - pA_y) * (pB_x - pD_x) + (pD_y - pB_y) * (pC_x - pA_x));
return k_x + ',' + k_y;
}
5、两条线的交点,不一定在线段上,有可能在线段的延长线上,所以需要判断交点是否在线段上
//判断 随机产生的点 和点X 的连线 与地图上已知的两点(给出的坐标中连续的两点)之间的连线 的 交点 是否在 已知的两点的线段之上 如果在之上:那么点X的顺序应该调整到已知的两点中间
function CrosspointIsOnTheLine(point1, point2, point3, point4)
{
var crossPoint = getCrossPoint(point1, point2, point3, point4);//交点坐标
var result = {
online: false,//是否在线段上
nearP2: undefined//如果不在线段上,是否近p2,否则近p3
};
//交点分别到 第2点 和 第3点 之间的距离 等于 第2点到第3点的距离 那么 交点在线段上
var cp_xy = crossPoint.split(',');
var p2_xy = point2.split(',');
var p3_xy = point3.split(',');
var cp_p2_length = getLength(cp_xy[0], cp_xy[1], p2_xy[0], p2_xy[1]);//交点到p2的距离
var cp_p3_length = getLength(cp_xy[0], cp_xy[1], p3_xy[0], p3_xy[1]);//交点到p3的距离
var p2_p3_length = getLength(p2_xy[0], p2_xy[1], p3_xy[0], p3_xy[1]);//p2到p3的距离
//由于线段的长度本身存在精度的问题 ,所以这么比较 交点到 p2和p3的距离 同时小于 p2到p3的距离 说明 交点在 p2到p3的线段上
if (cp_p2_length <= p2_p3_length && cp_p3_length <= p2_p3_length) {
result.online = true;
}
else {
//if (cp_p2_length > p2_p3_length) {
// result.nearP2 = false;
//}
//else if (cp_p3_length > p2_p3_length) {
// result.nearP2 = true;
//}
}
return result;
}
如图,A与多边形上的点构成的夹角是360°说明A在多边形内。
如图,点A与多边形上的点构成的夹角不是360°,说明A不在多边形内。 2、对于凹多边形来说,将凹的部分可能重复计算夹角的地方调整坐标在集合中的顺序后计算夹角。
在按照原理1会计算∠BAC加上∠CAD的值,如图,实际上∠CAD是是∠BAC的一部分,所以这里要么累加时不要包含∠CAD的值;要么调整CD两点的位置,利用原理1,计算∠BAD加上∠DAC(调整位置后就是∠CAD)。问题是,什么时候需要调整CD的位置,我们发现在原理1中,在多边形内的点与多边形上的点的连线与多边形边界没有交点,而该图有交点。 所以若第一个点A与地图上出去BC两点的任意一点D的连线,若与BC两点的连线存在交点,那么这是需要调整任意一点D与B的位置(或C的位置)。这个过程是对坐标集排序的过程。之后利用原理1即可。 五、代码实现(javascript): 我的博客园相关代码访问地址: http://www.cnblogs.com/langu/p/3458846.html http://www.cnblogs.com/langu/p/3458835.html 1、两个点间的距离 获取坐标轴内两个点间的距离 function getLength(point1_x, point1_y, point2_x, point2_y) { var diff_x = Math.abs(point2_x - point1_x); var diff_y = Math.abs(point2_y - point1_y); var length_pow = Math.pow(diff_x, 2) + Math.pow(diff_y, 2);//两个点在 横纵坐标的差值与两点间的直线 构成直角三角形。length_pow等于该距离的平方 return Math.sqrt(length_pow); } 2、获得三个点构成的三角形的 第一个点所在的角度的余弦值 function getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y) { var length1_2 = getLength(point1_x, point1_y, point2_x, point2_y);//获取第一个点与第2个点的距离 var length1_3 = getLength(point1_x, point1_y, point3_x, point3_y); var length2_3 = getLength(point2_x, point2_y, point3_x, point3_y); var res = (Math.pow(length1_2, 2) + Math.pow(length1_3, 2) - Math.pow(length2_3, 2)) / (length1_2 * length1_3 * 2);//cosA=(pow(b,2)+pow(c,2)-pow(a,2))/2*b*c return res; } var pi180 = 180 / Math.PI; 3、将余弦值转换为角度 //获取3个点的夹角,角顶点为第一个点 function getAngle(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y) { var _cos1 = getCos(point1_x, point1_y, point2_x, point2_y, point3_x, point3_y);//第一个点为顶点的角的角度的余弦值 return Math.acos(_cos1) * pi180; } 4、已知4个点的坐标,求两个线段的交点坐标。对应原理2中的ABCD四个点。 //判断第一个点 与 第四个点所连直线 与 第2个点和第3个点 所连直线的交点 是否在 第2个和第3个点的线段上 function getCrossPoint(point1, point2, point3, point4) { var pD_x = point1.split(',')[0]; var pD_y = point1.split(',')[1]; var pA_x = point2.split(',')[0]; var pA_y = point2.split(',')[1]; var pC_x = point3.split(',')[0]; var pC_y = point3.split(',')[1]; var pB_x = point4.split(',')[0]; var pB_y = point4.split(',')[1]; var k_y = (pB_x * pC_y * pD_y - pD_x * pB_y * pC_y - pA_y * pB_x * pD_y + pD_x * pB_y * pA_y + pC_x * pA_y * pD_y - pA_x * pC_y * pD_y - pC_x * pB_y * pA_y + pA_x * pB_y * pC_y) / (pD_y * pC_x - pA_x * pD_y - pB_y * pC_x + pA_x * pB_y + pB_x * pC_y - pD_x * pC_y - pA_y * pB_x + pA_y * pD_x); var k_x = (pD_y * (pC_x - pA_x) * (pB_x - pD_x) - pA_y * (pC_x - pA_x) * (pB_x - pD_x) + pA_x * (pC_y - pA_y) * (pB_x - pD_x) + pD_x * (pD_y - pB_y) * (pC_x - pA_x)) / ((pC_y - pA_y) * (pB_x - pD_x) + (pD_y - pB_y) * (pC_x - pA_x)); return k_x + ',' + k_y; } 5、两条线的交点,不一定在线段上,有可能在线段的延长线上,所以需要判断交点是否在线段上 //判断 随机产生的点 和点X 的连线 与地图上已知的两点(给出的坐标中连续的两点)之间的连线 的 交点 是否在 已知的两点的线段之上 如果在之上:那么点X的顺序应该调整到已知的两点中间 function CrosspointIsOnTheLine(point1, point2, point3, point4) { var crossPoint = getCrossPoint(point1, point2, point3, point4);//交点坐标 var result = { online: false,//是否在线段上 nearP2: undefined//如果不在线段上,是否近p2,否则近p3 }; //交点分别到 第2点 和 第3点 之间的距离 等于 第2点到第3点的距离 那么 交点在线段上 var cp_xy = crossPoint.split(','); var p2_xy = point2.split(','); var p3_xy = point3.split(','); var cp_p2_length = getLength(cp_xy[0], cp_xy[1], p2_xy[0], p2_xy[1]);//交点到p2的距离 var cp_p3_length = getLength(cp_xy[0], cp_xy[1], p3_xy[0], p3_xy[1]);//交点到p3的距离 var p2_p3_length = getLength(p2_xy[0], p2_xy[1], p3_xy[0], p3_xy[1]);//p2到p3的距离 //由于线段的长度本身存在精度的问题 ,所以这么比较 交点到 p2和p3的距离 同时小于 p2到p3的距离 说明 交点在 p2到p3的线段上 if (cp_p2_length <= p2_p3_length && cp_p3_length <= p2_p3_length) { result.online = true; } else { //if (cp_p2_length > p2_p3_length) { // result.nearP2 = false; //} //else if (cp_p3_length > p2_p3_length) { // result.nearP2 = true; //} } return result; }