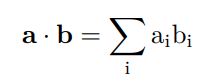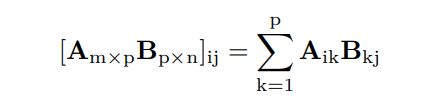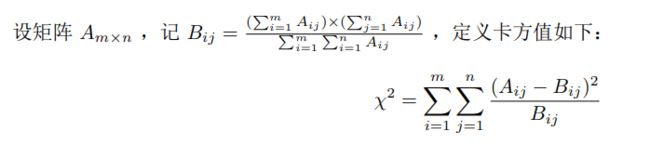Day1-Python-Numpy(Datawhale)

1. python基础

1.1 列表推导式与条件赋值

1.1.1 列表推导式

L = []  #创建空列表

def my_func(x): #定义函数my_func()
    return 2*x

for i in range(5): #for循环
    L.append(my_func(i))

print(L)

[0, 2, 4, 6, 8]

使用列表推导式[function for i in list]

function:映射函数,list：迭代的对象

[my_func(i) for i in range(5)]

[0, 2, 4, 6, 8]

列表表达式支持嵌套,第一个for为外层,第二个for为内层，在书写时可以先写for条件，再写迭代对象

[ m+'_'+n for m in ['a','b'] for n in ['c','d']]

['a_c', 'a_d', 'b_c', 'b_d']

上面嵌套查询等价于下面的for循环

result = []
for m in ['a','b']:
    for n in ['c','d']:
       f = m+'_'+n
       result.append(f)
print(result)

['a_c', 'a_d', 'b_c', 'b_d']

1.1.2 条件赋值

value = a if condition else b

value = 'cat' if 2>1 else 'dog'
print(value)

cat

a = 'cat'
b = 'dog'
condition = 2>1 #结果为布尔型True
if condition:
    value = a
else:
    value = b
print(value)

cat

截断列表中超过5的元素

L = [1, 2, 3, 4, 5, 6, 7]
    
value = [i for i in L if i <=5]
print(value)

[1, 2, 3, 4, 5]

j = []
for i in L :
    if i <=5:
        j.append(i)
print(j)  

[1, 2, 3, 4, 5]

将列表中超过5的元素替换为5

[i if i<=5 else 5 for i in L]

[1, 2, 3, 4, 5, 5, 5]

k = []
for i in L:
    if i<=5:
        k.append(i)
    else:
        k.append(5)
print(k)

[1, 2, 3, 4, 5, 5, 5]

**如果if和for同时使用，for在前，if在后；

若if…else…和for同时使用for在后，if在前

1.2 匿名函数与map方法

函数的定义具有清晰简单的映射关系，可以使用匿名函数

my_func_lambda = lambda x: 2*x
my_func_lambda(3)

6

multi_para_func = lambda a, b: a+b #求a+b的和
multi_para_func(1,2)

3

匿名函数使用在无需多次调用的场合

[(lambda x: 2*x)(i) for i in range(5)]

[0, 2, 4, 6, 8]

列表推导式的匿名函数映射使用map函数完成

list(map(lambda x: 2*x, range(5))) #使用list转换为列表

[0, 2, 4, 6, 8]

list(map(lambda x,y: str(x)+'_'+y, range(5), list('abcde')))
#对应位置的数据进行拼接

['0_a', '1_b', '2_c', '3_d', '4_e']

[(lambda x,y: str(x)+'_'+y)(x,y) for x,y in list(zip(range(5),list('abcde')))]

['0_a', '1_b', '2_c', '3_d', '4_e']

list(zip(range(5),list('abcde')))

[(0, 'a'), (1, 'b'), (2, 'c'), (3, 'd'), (4, 'e')]

1.2.1 zip对象与enumerate方法

zip将多个可迭代的对象打包称一个元组，返回zip对象，通过tuple,list得到相应结果

L1, L2, L3 = list('abc'), list('def'), list('hij')
list(zip(L1, L2, L3))

[('a', 'd', 'h'), ('b', 'e', 'i'), ('c', 'f', 'j')]

for i, j, k in zip(L1, L2, L3):
    print(i, j, k)

a d h
b e i
c f j

enumerate在迭代时绑定迭代元素的遍历序号

L = list('abcd')
for index, value in enumerate(L):
    print(index, value)

0 a
1 b
2 c
3 d

for index, value in list(zip(range(len(L)), L)):
    print(index, value)

0 a
1 b
2 c
3 d

对两个列表进行字典映射，可使用zip

dict(zip(L1,L2))

{'a': 'd', 'b': 'e', 'c': 'f'}

zipped = list(zip(L1, L2, L3))
zipped

[('a', 'd', 'h'), ('b', 'e', 'i'), ('c', 'f', 'j')]

zip(*zipped) *zipped参数，可以list数组，也可以是zip()函数返回的对象

list(zip(*zipped))

[('a', 'b', 'c'), ('d', 'e', 'f'), ('h', 'i', 'j')]

*zip()函数：zip()函数的逆过程，将zip对象变成原先组合前的数据

L11, L21, L31 = zip(*zip(L1, L2, L3)) 
print('L11, L21, L31分别是',L11, L21, L31)

L11, L21, L31分别是 ('a', 'b', 'c') ('d', 'e', 'f') ('h', 'i', 'j')

2. Numpy基础

2.1 np数组的构造

np.array构建

import numpy as np

np.array([1, 2, 3])

array([1, 2, 3])

等差序列

np.linspace(包含终止数),

np.arange(不包含终止数)

np.linspace(1,5,11) #从1到5，包含11个数,且包含5

array([1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6, 5. ])

np.arange(1, 5, 2) #从1到5，包含2个数，不包含5

array([1, 3])

特殊矩阵：

zeros:零矩阵

eye: 单位矩阵

full: 全矩阵

np.zeros((2,3))

array([[0., 0., 0.],
       [0., 0., 0.]])

np.eye(3)

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

np.eye(3, k=1) #偏移主对角线为1的伪单位矩阵

array([[0., 1., 0.],
       [0., 0., 1.],
       [0., 0., 0.]])

np.full((2,3), 10) #10为填充的数值

array([[10, 10, 10],
       [10, 10, 10]])

np.full((2,3), [1, 2, 3]) #传入列表填充值

array([[1, 2, 3],
       [1, 2, 3]])

随机矩阵: np.random

随机生成函数：rand(0-1均匀分布随机数组)、randn(标准正态随机数组)、randint(随机整数组)、choice(随机列表抽样)

np.random.rand(3) #生成服从0-1均匀分布的三个随机数

array([0.26409239, 0.37878376, 0.47260148])

np.random.rand(3,3) #生成3X3的服从0-1均匀分布的随机数组

array([[0.76192967, 0.80685473, 0.38614521],
       [0.74780002, 0.32637906, 0.33276572],
       [0.7977825 , 0.97219606, 0.71320856]])

服从区间a到b的均匀分布

a, b = 5, 15
(b - a) * np.random.rand(3)+a

array([11.27901368,  6.00345324,  5.2041489 ])

randn生成N(0,1)的标准正态分布

np.random.randn(3)

array([ 1.24890004, -0.86756835, -0.69481399])

np.random.randn(2,2)

array([[0.30693017, 0.93315798],
       [0.614196  , 2.11708677]])

标准正态化(X-miu)/sigma

sigma, miu = 2.5, 3

miu + np.random.randn(3) * sigma

array([-1.03226159,  8.14368631,  4.56748111])

randint: 生成随机整数的最小值最大值和维度大小(包含最小值和最大值)

low, high, size = 1, 15, (2,2) 

np.random.randint(low, high, size)

array([[8, 6],
       [9, 8]])

choice 从给定的列表中，以一定概率和方式抽取结果，不指定概率时为均匀抽样，默认为有放回

my_list = ['a', 'b', 'c', 'd']
np.random.choice(my_list, 2, replace = False, p=[0.1, 0.7, 0.1, 0.1])
#从my_list中抽取2个数，不放回抽取，a,b,c,d的概率分别时0.1，0.7，0.1，0.1

array(['b', 'c'], dtype='

当返回的元素的个数与原列表相同时，等价于使用permutation函数，即打散原列表

np.random.permutation(my_list)

array(['b', 'd', 'c', 'a'], dtype='

np.random.choice(my_list, 4, replace=False )

array(['b', 'a', 'd', 'c'], dtype='

随机种子seed, 固定随机数的输出结果

np.random.seed(0)
np.random.rand()

0.5488135039273248

np.random.seed(0)
np.random.rand()

0.5488135039273248

2.2 np数组的变形与合并

转置:T

np.zeros((2,3)).T

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

合并操作：r_,c_

二维数组：r_：上下合并

c_：左右合并

np.r_[np.eye(3),np.zeros((2,3))]

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.],
       [0., 0., 0.],
       [0., 0., 0.]])

np.c_[np.full((3,2),[2,3]),np.zeros((3,2))]

array([[2., 3., 0., 0.],
       [2., 3., 0., 0.],
       [2., 3., 0., 0.]])

一维数组进行合并时，在长度匹配时使用左右合并，一维数组视为列向量，不会进行上下合并

np.r_[np.array([1,2]),np.zeros(2)]

array([1., 2., 0., 0.])

np.c_[np.array([1,2,3]),np.zeros((3,3))]

array([[1., 0., 0., 0.],
       [2., 0., 0., 0.],
       [3., 0., 0., 0.]])

维度变换：reshape

将原数组按照新的维度重新排列，C模式：逐列；F模式：逐行

origin = np.arange(8)
target = np.arange(8).reshape(2,4) #默认按行读取
print(origin)
print(target)

[0 1 2 3 4 5 6 7]
[[0 1 2 3]
 [4 5 6 7]]

target.reshape((4,2), order='C')

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])

target.reshape((4,2), order = 'F') #按列读取

array([[0, 2],
       [4, 6],
       [1, 3],
       [5, 7]])

被调用的数组是确定的，reshape允许维度空缺，填充为-1即可

target.reshape((4,-1)) #确认读取4行，由于数组确定，则列一定为2

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])

target.reshape((-1,4)) #确定读取4列，由于数组确定，则行一定是2

array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

将n*1维数组转换为1维数组

target = np.ones((3,1))
target

array([[1.],
       [1.],
       [1.]])

target.reshape(1,-1) #1可以省略不写，即为reshape(-1)

array([[1., 1., 1.]])

2.3 np数组的切片与索引

数组的切片模式支持使用slice类型的start: end: step(开始: 结束: 步长)，也可直接传入列表指定某个维度的索引进行切片

target = np.arange(12).reshape(4,3)
target

array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

target[:-1,[0,2]] #选取0,2行的0,2列数

array([[0, 2],
       [3, 5],
       [6, 8]])

利用np.ix_在对应的维度上使用布尔索引，此时不能使用slice切片

np.ix_(行范围,列范围). 行范围和列范围都可以是布尔型或者列表

target[np.ix_([True, False, True, False], [True, False, True])]

array([[0, 2],
       [6, 8]])

target[np.ix_([0,2],[True, False, True])] #ix_(行范围,列范围)

array([[0, 2],
       [6, 8]])

target[np.ix_([True, False, True, False],[0,2])]

array([[0, 2],
       [6, 8]])

target[np.ix_([0,2],[0,2])]

array([[0, 2],
       [6, 8]])

数组维度为1维时，可直接进行布尔索引，无需np.ix_

new = target.reshape(-1)
new[[0,2]]

array([0, 2])

new[new%2==0] #是否为2的倍数

array([ 0,  2,  4,  6,  8, 10])

2.4 常见函数

where 条件函数，指定满足条件与不满足条件位置对应的填充

a = np.array([-1, 1, -1, 0])
np.where(a>0, a, 5) #满足a>0填充a，不满足填充5

array([5, 1, 5, 5])

nonzero: 返回非零的索引

argmax: 返回最大的索引

argmin: 返回最小的索引

a = np.array([-2, -5, 0, 1, 3, -1 ])
np.nonzero(a)

(array([0, 1, 3, 4, 5], dtype=int64),)

a.argmax()

4

a.argmin()

1

any: 当序列至少存在一个True或非零元素返回True, 否则返回False

all: 序列元素全为True或非零元素返回True,否则返回False

a = np.array([0,1])
a.any()

True

a.all()

False

cumprod: 累乘，返回同长度的数组

cumsum: 累加，返回同长度数组

diff: 和前一个元素作差，第一个元素为缺失值，默认参数情况下，返回长度是原数组-1

a = np.array([2, 3, 4])
a.cumprod()

array([ 2,  6, 24], dtype=int32)

a.cumsum()

array([2, 5, 9], dtype=int32)

np.diff(a)

array([1, 1])

统计函数

max,min,mean,median,std,var,sum,quantile(分位数)。分位数计算属于全局方法，使用np.quantile()

target = np.arange(5)
print(target)
target.max()

[0 1 2 3 4]





4

np.quantile(target,0.5) #0.5分位数

2.0

含有缺失值的数组，返回结果也是缺失结果，若需要省略缺失值，使用nan*类型函数

nanmax,nanmin,nanmean,nanmedian,nanstd,nanvar,nansum,nanquantile

target = np.array([1, 2, np.nan])
print(target)
target.max()

[ 1.  2. nan]





nan

np.nanmax(target)

2.0

np.nanquantile(target,0.5)

1.5

协方差: cov

相关系数: corrcoef

target1 = np.array([1, 3, 5, 9])
target2 = np.array([1, 5, 3, -9])

np.cov(target1, target2)

array([[ 11.66666667, -16.66666667],
       [-16.66666667,  38.66666667]])

np.corrcoef(target1, target2)

array([[ 1.        , -0.78470603],
       [-0.78470603,  1.        ]])

统计函数的axis参数，能够进行某一维度下的统计特征计算，当axis=0时结果为列的统计指标，aixs=1时结果为行的统计指标

target = np.arange(1, 10).reshape(3,-1)
target

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

target.sum(0) #axis=0,按列进行求和

array([12, 15, 18])

target.sum(1) #axis=1,按行进行求和

array([ 6, 15, 24])

2.5 广播机制

用来处理两个不同维度数组之间的操作

标量和数组的操作

当一个标量和数组进行运算时，标量会自动将大小扩充为数组的大小，之后进行逐元素操作

res = 3 * np.ones((2,2))+1
res

array([[4., 4.],
       [4., 4.]])

res = 1/res
res

array([[0.25, 0.25],
       [0.25, 0.25]])

二维数组之间的操作

维度完全一致：使用对应元素的操作，否则会报错。

当其中一个数组的维度为 m×1或者 1×n，会将具有1的维度扩充为另一个数组对应的维度，但是m、n要与数组的维度一致

res = np.ones((3,2))
res

array([[1., 1.],
       [1., 1.],
       [1., 1.]])

res * np.array([2,3])
#np.arrray([2,3])是1×2的一位数组，res为3×2的数组,前面的1变为3，达到相同维度

array([[2., 3.],
       [2., 3.],
       [2., 3.]])

res * np.array([[2],[3],[4]])
#np.array([[2],[3],[4]])为3×1，res为3×2，因此1会变为2

array([[2., 2.],
       [3., 3.],
       [4., 4.]])

res * np.array([[2]])
#np.array([[2]])为1×1，所以前面的1变为3，后面的变为2，变为3×2数组

array([[2., 2.],
       [2., 2.],
       [2., 2.]])

一维数组与二维数组的操作

一维数组A(k)与二维数组B(m,n)，将A(k)视为A(1,k)的二维数组，当k != n且k,n都不是1时报错

np.ones((2,3))

array([[1., 1., 1.],
       [1., 1., 1.]])

np.ones(3)

array([1., 1., 1.])

np.ones(3) + np.ones((2,3))

array([[2., 2., 2.],
       [2., 2., 2.]])

np.ones((2,1))

array([[1.],
       [1.]])

np.ones(1) + np.ones((2,3))

array([[2., 2., 2.],
       [2., 2., 2.]])

2.6 向量与矩阵的计算

向量内积: dot

a = np.array([1, 2, 3])
b = np.array([1, 3, 5])
a.dot(b)

22

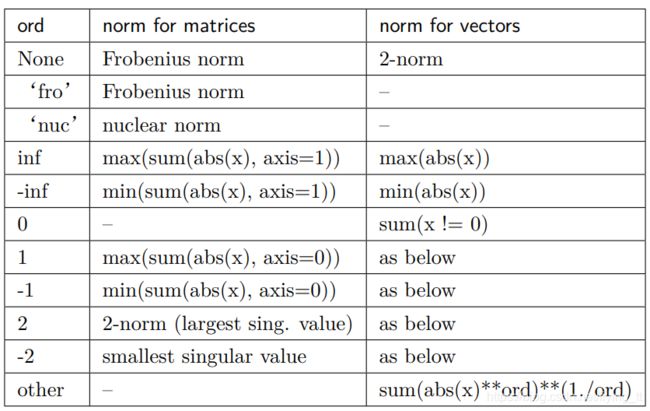
向量范数和矩阵范数: np.linalg.norm

重要的时ord参数，可选值如下：

matrix_target = np.arange(4).reshape(-1,2)
matrix_target

array([[0, 1],
       [2, 3]])

np.linalg.norm(matrix_target,'fro')

3.7416573867739413

np.linalg.norm(matrix_target, np.inf)

5.0

vector_target = np.arange(4)
vector_target

array([0, 1, 2, 3])

np.linalg.norm(vector_target, np.inf)

3.0

np.linalg.norm(vector_target, 2)

3.7416573867739413

np.linalg.norm(vector_target, 3)

3.3019272488946263

矩阵乘法: @

a = np.arange(4).reshape(-1,2)
a

array([[0, 1],
       [2, 3]])

b = np.arange(-4,0).reshape(-1,2)
b

array([[-4, -3],
       [-2, -1]])

a@b

array([[ -2,  -1],
       [-14,  -9]])

3. 练习

3.1 利用列表推导式写矩阵乘法

将矩阵乘法改写为列表推导式

M1 = np.random.rand(2,3)
M1

array([[0.71518937, 0.60276338, 0.54488318],
       [0.4236548 , 0.64589411, 0.43758721]])

M2 = np.random.rand(3,4)
M2

array([[0.891773  , 0.96366276, 0.38344152, 0.79172504],
       [0.52889492, 0.56804456, 0.92559664, 0.07103606],
       [0.0871293 , 0.0202184 , 0.83261985, 0.77815675]])

res = np.empty((M1.shape[0], M2.shape[1]))
#empty()数组的元素不为空，为随机产生的数据
#M1.shape[0]返回M1的行数
#M2.shape[1]返回M2的列数
res

array([[-3.5, -1.5,  0.5,  4.5],
       [ 1. ,  5. ,  3. , -9. ]])

for i in range(M1.shape[0]):
    for j in range(M2.shape[1]):
        item = 0
        for k in range(M1.shape[1]):
            item += M1[i][k] * M2[k][j]
        res[i][j] = item
print(res)

[[1.00406034 1.04261448 1.2858296  1.03305579]
 [0.75754069 0.7840043  1.12462806 0.72181133]]

M1@M2

array([[1.00406034, 1.04261448, 1.2858296 , 1.03305579],
       [0.75754069, 0.7840043 , 1.12462806, 0.72181133]])

((M1@M2 - res) < 1e-15).all()

True

np.array([[sum([M1[i][k]*M2[k][j] for k in range(M1.shape[1])]) for j in range(M2.shape[1])] for i in range(M1.shape[0])])

array([[1.00406034, 1.04261448, 1.2858296 , 1.03305579],
       [0.75754069, 0.7840043 , 1.12462806, 0.72181133]])

x = np.arange(6).reshape(-1,3)
x

array([[0, 1, 2],
       [3, 4, 5]])

y = np.arange(12).reshape(-1,4)
y

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

x@y

array([[20, 23, 26, 29],
       [56, 68, 80, 92]])

在这个地方得到的是数组，无法将数组的结果求和，最后发现在第二个循环时，需要将第三个循环进行一次求和

[[[(x[i][k]*y[k][j]) for k in range(3)] for j in range(4)] for i in range(2) ]

[[[0, 4, 16], [0, 5, 18], [0, 6, 20], [0, 7, 22]],
 [[0, 16, 40], [3, 20, 45], [6, 24, 50], [9, 28, 55]]]

np.array([[sum([(x[i][k]*y[k][j]) for k in range(3)]) for j in range(4)] for i in range(2)])

array([[20, 23, 26, 29],
       [56, 68, 80, 92]])

3.2 更新矩阵

思路：先求出1/A的值，再将A(i,j)与1/A相乘。刚开始考虑的是使用for循环去遍历矩阵的值。之后发现本质上就是矩阵的求和

A = np.arange(1,10).reshape(3,3)
A

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

B = np.zeros(9).reshape(3,3)
B

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

 [[ sum([A[i][j]/A[i][k] for k in range(A.shape[0])]) for j in range(A.shape[1])] for i in range(A.shape[0])]

[[1.8333333333333333, 3.6666666666666665, 5.5],
 [2.466666666666667, 3.0833333333333335, 3.7],
 [2.6527777777777777, 3.0317460317460316, 3.4107142857142856]]

for i in range(3):
    for j in range(3):
        for k in range(3):
            B[i][j] += A[i][j]/A[i][k]
B

array([[1.83333333, 3.66666667, 5.5       ],
       [2.46666667, 3.08333333, 3.7       ],
       [2.65277778, 3.03174603, 3.41071429]])

A1 = np.arange(1,10).reshape(3,3)
A1

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

A1.sum(1)

array([ 6, 15, 24])

A1.sum(1).reshape(-1,1) 

array([[ 6],
       [15],
       [24]])

A1*(1/A1).sum(1).reshape(-1,1) 

array([[1.83333333, 3.66666667, 5.5       ],
       [2.46666667, 3.08333333, 3.7       ],
       [2.65277778, 3.03174603, 3.41071429]])

3.3 卡方统计量

思路：首先需要将B(i,j)的值求解出来，用A的列×A的行，再除以A的行列和

np.random.seed(0)

A = np.random.randint(10, 20, (8,5))

A

array([[15, 10, 13, 13, 17],
       [19, 13, 15, 12, 14],
       [17, 16, 18, 18, 11],
       [16, 17, 17, 18, 11],
       [15, 19, 18, 19, 14],
       [13, 10, 13, 15, 10],
       [12, 13, 18, 11, 13],
       [13, 13, 17, 10, 11]])

B = A.sum(0)*A.sum(1).reshape(-1,1)/A.sum()
K = ((A-B)**2/B).sum()
K

11.842696601945802

3.4 改进矩阵计算的性能

需要将等式变形后，根据矩阵的相关知识进行求解。

np.random.seed(0)
m, n, p = 100, 80, 50
B = np.random.randint(0, 2, (m,p)) #0-2之间的100×50的矩阵
U = np.random.randint(0, 2, (p,n)) 
Z = np.random.randint(0, 2, (m,n))

def solution(B, U, Z):
    L_res = []
    for i in range(m):
        for j in range(n):
            norm_value = ((B[i]-U[:,j])**2).sum()
            L_res.append(norm_value*Z[i][j])
        return sum(L_res)

solution(B, U, Z)

882

(((B**2).sum(1).reshape(-1,1) + (U**2).sum(0) - 2*B@U)*Z).sum()

100566

3.5 连续整数的最大长度

思路：通过作差之后差值为1判断是否为连续数组，然后通过不为1的索引位置作差得到连续数组的长度

x = [1,2,3,4,7,8,9]
np.diff(x) #作差

array([1, 1, 1, 3, 1, 1])

np.r_[1, np.diff(x)!=1, 1 ]

array([1, 0, 0, 0, 1, 0, 0, 1], dtype=int32)

np.nonzero(np.r_[1, np.diff(x)!=1,1]) #返回非零元素的索引值数组

(array([0, 4, 7], dtype=int64),)

np.diff(np.nonzero(np.r_[1, np.diff(x)!=1,1])).max()

4

f = lambda x : np.diff(np.nonzero(np.r_[1, np.diff(x)!=1,1])).max()

f([1,3,4,5,7,8])

3