算法题(2) Levenshtein编辑距离和编辑方案

Levenshtein编辑距离和编辑方案

  问题描述：在应用领域中，经常会遇到对两个字符串进行比较的问题，比如在自然语言处理中，需要比较两个句子的相似度，高级点的方法有神经网络、TF-IDF文本相似度等，最基础的方法就是编辑距离了，最初它是由俄罗斯科学家Vladimir Levenshtein在1965年提出来的。它的解释是给定一个原字符串和一个目标字符串，计算将原字符串修改为目标字符串时所编辑的最小次数。编辑可以是“增加”、“删除”和“修改”三种。

  思路：本题需要动态规划思想，即对两个长字符串分别由小到大“部分计算”，直到最后完成全部的编辑。首先我们创建一个表格（可以用二维数组存储），其规格为（m+1）×（n+1），m、n分别为两个字符串的长度。我们假设原字符串是“kitten”，目标字符串是“sitting”，将原字符串设置为横向表头，将目标字符串设置为纵向表头（也可以反过来设置），则我们创建一个7×8的表格，如下所示：

	<\b>	k	i	t	t	e	n
<\b>
s
i
t
t
i
n
g

  表格创建完成后，我们开始编辑距离算法。

1、初始化： 首先我们对表格执行初始化，方法是将<\b>所对应的每一行、列都从0开始，置为递增的整数，即0，1，2…m或n. 如下图：

Edit-Dist	<\b>	k	i	t	t	e	n
<\b>	0	1	2	3	4	5	6
s	1
i	2
t	3
t	4
i	5
n	6
g	7

  解释：表格中的数字表示当前步骤时所编辑的次数，由于我们设置横向为原字符串，纵向为目标字符串，因此<\b>行的数字代表删除操作，<\b>列的部分代表插入操作。比如"kitten"中的"e"所对应的数字"5"，指的是在编辑时先将"kitten"中的“kitte”删除时的5个删除操作；“sitting”中的"n"对应的“6”代表编辑时先插入“sittin”时的6次插入操作。

2、填充表格： 接下来我们填充表格剩余的空白部分，方法如下：首先比较当前位置Matrix[i][j]所对应的列头、行头的字符是否相同，相同则当前位置取Matrix[i][j-1]+1、Matrix[j][i-1]+1和Matrix[i-1][j-1]的最小值，否则取Matrix[i][j-1]+1、Matrix[j][i-1]+1和Matrix[i-1][j-1]+1的最小值。公式如下：
$$Matrix[i][j]=min(Matrix[i][j-1]+1,Matrix[i-1][j]+1,Matrix[i-1][j-1]+f(i,j))$$
其中$f(i,j)$为特征函数，其计算方法为：
$$f(i,j)=\{\begin{array}{ll}0,& \text{source[j-1]=target[i-1]}\\ 1,& \text{else}\end{array}$$
  通过上述方法得出距离矩阵如下图：

Edit-Dist	<\b>	k	i	t	t	e	n
<\b>	0	1	2	3	4	5	6
s	1	1	2	3	4	5	6
i	2	2	1	2	3	4	5
t	3	3	2	1	2	3	4
t	4	4	3	2	1	2	3
i	5	5	4	3	2	2	3
n	6	6	5	4	3	3	2
g	7	7	6	5	4	4	3

  解释：由Matrix[i][j-1]至Matrix[i][j]的为插入操作，由Matrix[i-1][j]至Matrix[i][j]的为删除操作，由Matrix[i-1][j-1]至Matrix[i][j]的为修改操作（字符相同时不必修改，编辑步数不改变）。

3、最小编辑距离：
  我们通过Levenshtein距离算法对表格实现了填充，编辑距离为表格最右下角的数字。因此"kitten"到"sitting"的最小编辑距离是3.
4、枚举所有编辑方案：
  我们还可以通过算法列出达到最小编辑距离的所有编辑方案。编辑方案的计算需要“跳转列表”作为工具。跳转列表的生成规则是：如果当前值Matrix[i][j]=Matrix[i-1][j]+1，则我们认为当前状态可以通过行向下跳转过来，即可以执行一步插入操作；如果当前值Matrix[i][j]=Matrix[i][j-1]+1，则我们认为当前状态可以通过列向右跳转过来，即可以执行一步删除操作；如果当前值Matrix[i][j]=Matrix[i-1][j-1]+1且Matrix[i][j]对应行列的两个字符不相同，则我们认为当前状态可以通过左上方跳转过来，即可以执行一次修改操作；如果当前值Matrix[i][j]=Matrix[i-1][j-1]且Matrix[i][j]对应行列的两个字符相同，则我们认为当前状态可以通过左上方跳转过来，只不过这次由于字符相同，对应的操作是跳过。
   通过上述算法，我们生成上文给出的两个字符串的跳转列表如下：

Steps	<\b>	k	i	t	t	e	n
<\b>	-	→	→	→	→	→	→
s	↓	↘	→ ↘	→ ↘	→ ↘	→ ↘	→ ↘
i	↓	↓ ↘	↘	→	→	→	→
t	↓	↓ ↘	↓	↘	→ ↘	→	→
t	↓	↓ ↘	↓	↓ ↘	↘	→	→
i	↓	↓ ↘	↓ ↘	↓	↓	↘	→ ↘
n	↓	↓ ↘	↓	↓	↓	↓ ↘	↘
g	↓	↓ ↘	↓	↓	↓	↓ ↘	↓

  上述列表中有的单元格中具备多个跳转途径，表明当前状态可以从多个状态跳转过来，且都是编辑距离最小的方案。有了上述列表，我们可以枚举出所有的编辑方案，从表格左上角的‘-’出发，按照箭头合法的方向行进，直到到达右下角为止，则这条路径就是合法的编辑方案。最小距离编辑方案可能有很多种。

  下面我们展示Levenshtein编辑距离的Python实现代码：

class solution:

    def __init__(self, source, target):
        self.source = source
        self.target = target
        self.Matrix = []
        self.jump = []
        self.steps = []
        self.edit_distance(self.source, self.target)
        self.edit_steps()

    def edit_distance(self, source, target):
        if len(target) == 0 and len(source) == 0:
            return 0
        row = []
        jump_row = []
        for i in range(len(target)+1):
            row.append(i)
            if i == 0 :
                jump_row.append(['-'])
            else:
                jump_row.append(['↓'])
            for j in range(len(source)):
                if i == 0 :
                    row.append(j+1)
                    jump_row.append(['→'])
                    continue
                else:jump_row.append([])
                row.append(0)
            self.Matrix.append(row)
            self.jump.append(jump_row)
            jump_row=[]
            row=[]
        for i in range(1, len(target)+1):
            for j in range(1, len(source)+1):
                if target[i-1] == source[j-1] : edit = 0
                else : edit = 1
                self.Matrix[i][j] = min(self.Matrix[i-1][j]+1, self.Matrix[i][j-1]+1, self.Matrix[i-1][j-1]+edit)
                if self.Matrix[i][j] == self.Matrix[i-1][j]+1:
                    self.jump[i][j] = ['↓']
                if self.Matrix[i][j] == self.Matrix[i][j-1]+1:
                        self.jump[i][j].append('→')
                if self.Matrix[i][j] == self.Matrix[i-1][j-1] and self.source[j-1] == self.target[i-1]:
                        self.jump[i][j].append('↘')
                if self.Matrix[i][j] == self.Matrix[i-1][j-1]+1 and self.source[j-1] != self.target[i-1]:
                        self.jump[i][j].append('↘')
        for i in range(len(target)+1):
            print(self.Matrix[i])
        for i in range(len(target)+1):
            print(self.jump[i])

    def search(self, row, col, step):
        if row == len(self.target) and col == len(self.source) :
            self.steps.append(list(step))
            return 0
        jump = self.jump
        if row < len(self.target) and '↓' in jump[row+1][col]:
            step.append(self.target[:row+1]+self.source[col:])
            self.search(row+1, col, step)
            del step[-1]
        if col < len(self.source) and '→' in jump[row][col+1]:
            step.append(self.target[:row]+self.source[col+1:])
            self.search(row, col+1, step)
            del step[-1]
        if row < len(self.target) and col < len(self.source) and '↘' in jump[row+1][col+1]:
            if len(step) != 0 and self.target[:row+1]+self.source[col+1:] == step[-1]:
                self.search(row + 1, col + 1, step)
            else:
                step.append(self.target[:row+1]+self.source[col+1:])
                self.search(row + 1, col+1, step)
                del step[-1]
        return 0
    def edit_steps(self):
        if len(self.jump) == 0: return 0
        self.search(0, 0, [self.source])
        for i in range(len(self.steps)):
            print(f'方案{i+1}:', self.steps[i])

if __name__ == '__main__':
    edit = solution('kitten','sitting')

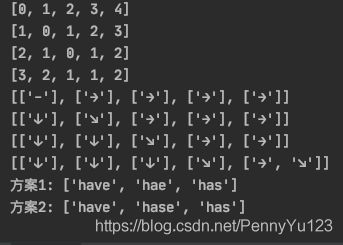
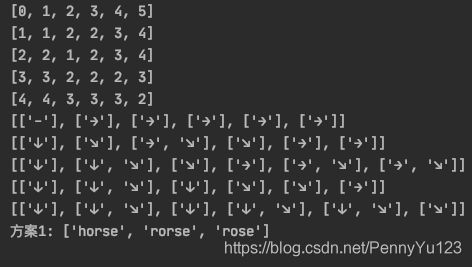
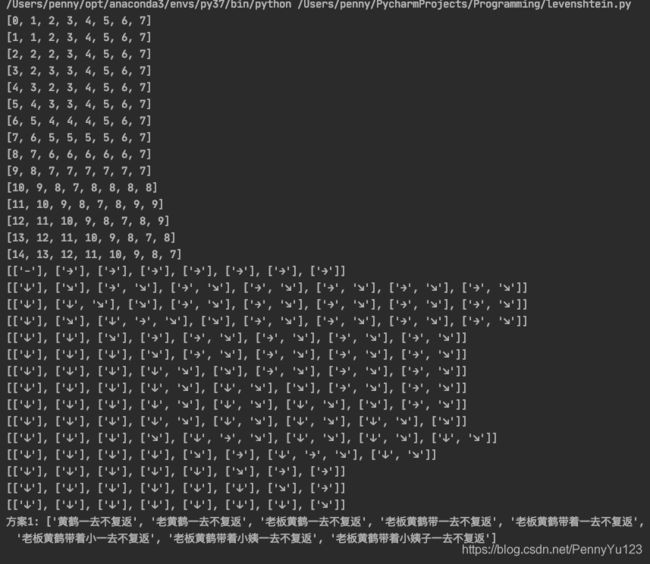
  代码可以输出编辑距离矩阵、跳转矩阵和所有符合要求的编辑方案。运行结果如下：

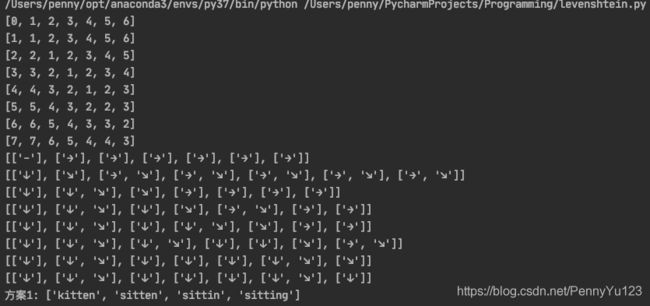
  注：字符串的编辑距离都是对称的，即字符串A到字符串B的最小编辑距离也是字符串B到字符串A的最小编辑距离。如果我们在代码中将“kitten”和“sitting”的位置互换，则编辑距离矩阵、跳转矩阵都会变为原来的转置。

  我们再用其他的字符串来验证算法的有效性，结果如下：








  可以看出，以上测试结果均同正确答案相符。