Python学习笔记：插入排序，希尔排序和堆排序的实现

自己动手写了一些方法用于实现插入排序（insertion sort），希尔排序（Shell sort）和堆排序（heap sort），其中希尔排序使用的增量序列为Hibbard增量。

import math

class MySort(object):
    def __init__(self, array):
        self.array = array
        self.N = len(array)
    def __del__(self):
        self.array = []
        self.N = 0
    def insertionsort(self):
        for i in range(1, self.N):
            temp = self.array[i]
            j = i
            for j in range(i - 1, -1, -1):
                if self.array[j] > temp:
                    self.array[j + 1] = self.array[j]
                else:
                    j += 1
                    break
            self.array[j] = temp
    def shellsort(self):
        k = int(math.log(self.N + 1, 2))
        increment = 2 ** k - 1
        while(increment > 0):
            for i in range(increment, self.N):
                temp = self.array[i]
                j = i
                for j in range(i - increment, -1, -increment):
                    if self.array[j] > temp:
                        self.array[j + increment] = self.array[j]
                    else:
                        j += increment
                        break
                self.array[j] = temp
            k -= 1
            increment = 2 ** k - 1
    def heapsort(self):
        for i in range(self.N // 2, -1, -1):
            self._percdown(i, self.N)
        for i in range(self.N - 1, 0, -1):
            temp = self.array[0]
            self.array[0] = self.array[i]
            self.array[i] = temp
            self._percdown(0, i)
    def _percdown(self, i, N):
        temp = self.array[i]
        while (self._leftchild(i) < N):
            child = self._leftchild(i)
            if child != N - 1 and self.array[child + 1] > self.array[child]:
                child += 1
            if temp < self.array[child]:
                self.array[i] = self.array[child]
            else:
                break
            i = child
        self.array[i] = temp
    def _leftchild(self, i):
        return 2 * i + 1

对这些方法进行测试：

import math, timeit, random
_array_test = [random.randint(0, 1000) for i in range(1, 100)]
def test():
    if __name__ == "__main__":
        print "unsorted array:", _array_test
        mysort = MySort(_array_test)
        mysort.insertionsort()
        print "sorted array:", mysort.array
        fromstr = "from sortmethods1 import _array_test, MySort"
        insertion = timeit.Timer("MySort(_array_test).insertionsort()", fromstr)
        shell = timeit.Timer("MySort(_array_test).shellsort()", fromstr)
        heap = timeit.Timer("MySort(_array_test).heapsort()", fromstr)
        print("insertion time: %s" % insertion.timeit(1000))
        print("shell time: %s" % shell.timeit(1000))
        print("heap time: %s" % heap.timeit(1000))

test()

当数组长度为100时，明显，插入排序耗时较少；

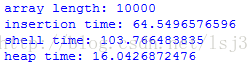
接下来对上述测试方法稍作修改，做了一组对比测试：

由此可看出，随着数组长度的成倍增加，堆排序的优势越来越明显。