时间序列预测之区间预测方法（PIs:MVE&Delta&Bayesian&Bootstrap&LUBE）

---

博主最近在入门时间序列预测的区间预测方法，网上关于区间预测方法的总结博客甚少，因此在阅读了一些论文之后，博主简单的对区间预测方法进行了总结，为的是给大家的入门提供一个参考。

所有内容的是从我自己的总结文档中截取的
不足之处，欢迎指正。

前言

传统的点预测，不能很好的处理系统运行中的不确定性，为了获得数值估计及其可靠性，实际应用对预测区间（PIs）的构造提出了很高的要求。区间预测方法的好坏要考察以下几个点：1）实施的难度；2）是否有关于数据分布的前提假设；3）计算量的大小（计算负担太大的方法无法满足实时性的要求）。本文的目的是提供一个宏观的入门参考指南，给小白的入门提供参考，如果读者是为了深入的进行预测区间的研究，在本文阅读的基础上还要进行大量的文献阅读。为了方便读者深入研究，博主在博客末尾简单的列写了一些参考文献。在方法的综述之前，我们写介绍一些预测区间的评价指标，为后面的方法综述提供基础。

一、预测区间的评价指标

1.PICP(PI coverage probability)

真实值落在预测区间上下界的比率

2.PINAW(PI normalized averaged width)

3.CWC(coverage width-based criterion)

CWC有时候也称为CLC(coverage-length-based criterion)

4.ACE(average coverage error)

5.AIS(average interval score)

6.MPICD(mean PI centre deviation)

两个不同的PI如果都覆盖了一个点，那么这个点越接近PI的中线则说明PI的质量越好。如下图所示：

二、区间预测方法综述

1.Mean Variance Estimation(MVE)

前提假设：误差的分布是具有非常数方差的加性高斯分布
缺点：准确度很大程度受到与其相关的数值预测的效果影响，计算负担相对小但是对于数据方差的低估会导致预测区间对真实数据的覆盖率低。
该方法考虑用一个NN来估计目标值的方差，然后用两个NN模型来构造预测区间。下面是MVE方法的原理图：

2.Delta Method

前提假设：对于每一个采样点，噪声的方差是恒定的，明显与实际是不符的。它还假设了多层前馈NNs是非线性回归模型，且能够用泰勒级数展开来线性化。
缺点：准确度很大程度受到与其相关的数值预测的效果影响
该方法基于NNs作为非线性模型的表示和解释，这将允许标准渐进理论应用于PI的构建。考虑如下回归式子：

3.Bayesian Method

前提假设：NN的每个参数都是一个分布，因此该网络的输出可以被看成观察训练数据的某种条件分布。
缺点：计算负担大，需要进行Hessian矩阵的计算，当数据规模不够大的时候，准确度很大程度依赖于先验知识。

4.Bootstrap Method

前提假设：假设噪声遵循零均值的正态分布
缺点：作为一种重采样方法，要训练很多不同的NN，对大数据集来说需要很大的计算成本。集成的性能很大程度取决于单独的网络，也就是说如果一个单独的网络偏差比较大，那么整个模型的性能就会恶化。

5.LUBE method

LUBE方法时为了克服上述四个方法的缺点而提出的，它没有对于数据分布的假设，也避免了Jacobian矩阵和Hessian矩阵数值计算的问题。
缺点：由于无法构建监督学习问题，LUBE方法中NNs的参数必须配合启发式的参数搜索方法来进行整定（包括NN的结构和参数），由于参数初始化没有一个特别好的方法，这大大增加了计算负担。
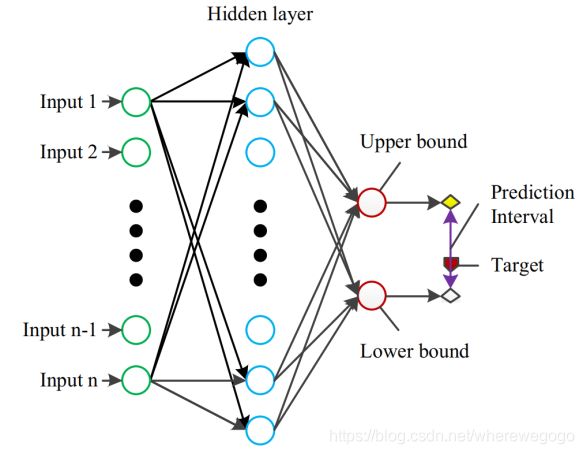
LUBE的方法是用NN分别输出PI的上界和下界（注意这里是用一个NN来预测两个输出），这种方法来获得预测区间是直接的。下面是LUBE方法的原理示意图：

总结

本文对五种区间预测的基本方法进行了总结，并且分析其假设和优缺点，包括：MVE方法、Delta方法、Bayesian方法、Bootstrap方法和LUBE方法。并且列总结了评价预测区间好坏的几种指标。本文可以作为了解区间预测基本方法的一种入门参考指南，如果要进行深入研究，还是要阅读相关的论文。

参考文献

[1] J. G. Hwang & A. A. Ding. Prediction intervals for artificial neural networks. Journal of the American Statistical Association. 1997, 92(438), 748-757.
[2] T. Heskes. Practical confidence and prediction intervals. In Advances in neural information processing systems. 1997, 176-182.
[3] G. Tang, Y. Wu, C. Li, P. K. Wong, Z. Xiao & X. An. A Novel Wind Speed Interval Prediction based on Error Prediction Method. IEEE Transactions on Industrial Informatics. 2020, 16(11), 6806-6915.
[4]A. Khosravi & S. Nahavandi. An optimized mean variance estimation method for uncertainty quantification of wind power forecasts. International Journal of Electrical Power & Energy Systems. 2014, 61, 446-454.
[5] C. Lian, L. Zhu, Z. Zeng, Y. Su, W. Yao & H. Tang. Constructing prediction intervals for landslide displacement using bootstrapping random vector functional link networks selective ensemble with neural networks switched. Neurocomputing. 2018, 291, 1-10.
[6] A. Khosravi, S. Nahavandi & D. Creighton. Construction of optimal prediction intervals for load forecasting problems. IEEE Transactions on Power Systems. 2010, 25(3), 1496-1503.
[7] Z. Han, W. Pedrycz, J. Zhao & W. Wang. Hierarchical Granular Computing-Based Model and Its Reinforcement Structural Learning for Construction of Long-Term Prediction Intervals. IEEE Transactions on Cybernetics. 2020
[8] C. Guan, P. B. Luh, L. D. Michel & Z. Chi. Hybrid Kalman filters for very short-term load forecasting and prediction interval estimation. IEEE Transactions on Power Systems. 2013, 28(4), 3806-3817.
[9] C. Lian, Z. Zeng, X. Wang, W. Yao, Y. Su & H. Tang. Landslide displacement interval prediction using lower upper bound estimation method with pre-trained random vector functional link network initialization. Neural Networks. 2020, 130, 286-296.
[10] A. Khosravi, S. Nahavandi, D. Creighton & A. F. Atiya. Lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE transactions on neural networks. 2010, 22(3), 337-346.
[11] N. A. Shrivastava, A. Khosravi & B. K. Panigrahi. Prediction interval estimation of electricity prices using PSO-tuned support vector machines. IEEE Transactions on Industrial Informatics. 2015, 11(2), 322-331.
[12] C. Sheng, J. Zhao, W. Wang & H. Leung. Prediction intervals for a noisy nonlinear time series based on a bootstrapping reservoir computing network ensemble. IEEE Transactions on neural networks and learning systems. 2013, 24(7), 1036-1048.
[13] C. Lian, C. P. Chen, Z. Zeng, W. Yao & H. Tang. Prediction intervals for landslide displacement based on switched neural networks. IEEE Transactions on Reliability. 2016, 65(3), 1483-1495.
[14] H. Quan, D. Srinivasan & A. Khosravi. Short-term load and wind power forecasting using neural network-based prediction intervals. IEEE transactions on neural networks and learning systems. 2013, 25(2), 303-315.
[15] A. Khosravi, E. Mazloumi, S. Nahavandi, D. Creighton & J. W. C. Van Lint. Prediction intervals to account for uncertainties in travel time prediction. IEEE Transactions on Intelligent Transportation Systems. 2011, 12(2), 537-547.