预测从瞎猜开始
按上一篇文章所说,机器学习是应用数学方法在数据中发现规律的过程。既然数学是对现实世界的解释,那么我们回归现实世界,做一些对照的想象。
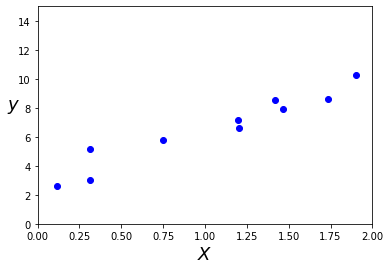
想象我们面前有一块塑料泡沫做的白板,白板上分布排列着数枚蓝色的图钉,隐约地它们似乎存在着某种规律,我们试着找出规律。
白板上的图钉(数据)如上图所示,我们有没有一种方法(数学算法)来寻找规律(模型解释)呢? 既然不知道怎么做,那我们瞎猜吧!
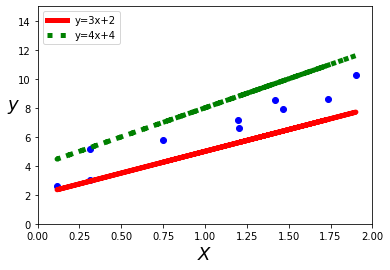
我拿起两根木棒在白板前比划,试着用木棒表示数据的规律。我随便放了放,如下图所示:
它们似乎都在一定程度上能表示蓝色图钉的规律,那么问题来了,绿色(虚线)和红色(实线)哪一个表示更好呢?
损失函数(成本函数)
好与坏是很主观的表达,主观的感受是不可靠的,我们必须找到一种客观的度量方式。我们想当然的认为误差最小的表示,是最好的。那么,我们引出一种量化误差的方法---最小二乘法。
最小二乘法:使误差的平方和最小的办法,是一种误差统计方法,二乘就是平方的意思。
$$ SE = \sum{(y_{pred} -y_{true})^2} $$
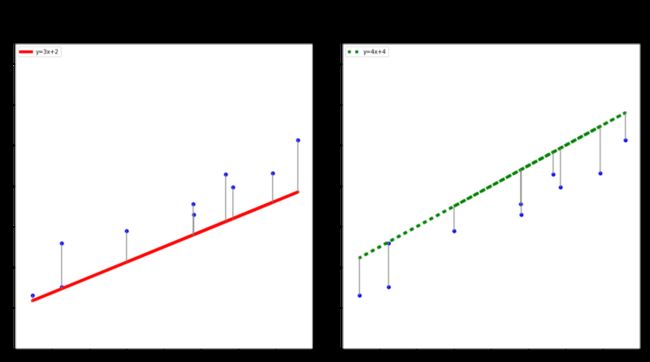
最小二乘法的解释是这样的,我们用预测值-实际值表示单点的误差,再把它们的平方和加到一起来表示整体误差。(平方的好处可以处理掉负数值,用绝对值的和也不是不可以。)我们用这个最终值来表示损失(成本),而可以表示损失(成本)的函数就叫做损失函数(成本函数)。
如上图我们可以看到,蓝色点到实线的距离就是我们要带入公式的误差。虽然它们看上去相近,但经过计算的结果是红色实线(y=3x+2)的损失为27.03,而绿色实线(y=4x+4)的损失为29.54,显然红色模型优于绿色模型。
那么,还有没有比红色实线更好的模型来表示数据呢?有没有一种方式来找到它呢?
梯度下降
我们把木棒(实线、模型)的表示数学化,我们既然可以用3、4做为x的系数,那我们当然可以尝试别的数字。我们用如下公式表示这种关系:
$$ y = wx + b $$
其中,x和y是已知的,我们不断调整w(权重)和b(偏差),然后再带入损失函数以求得最小值的过程,就是梯度下降。
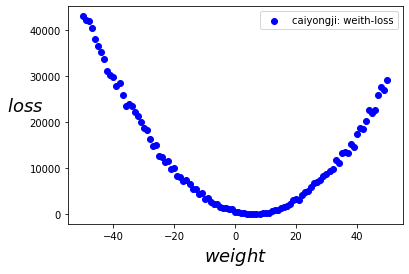
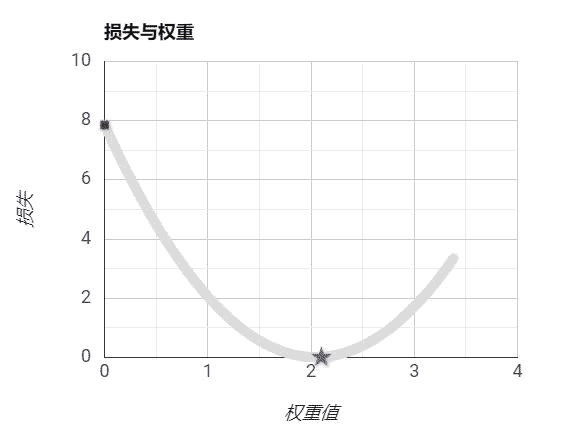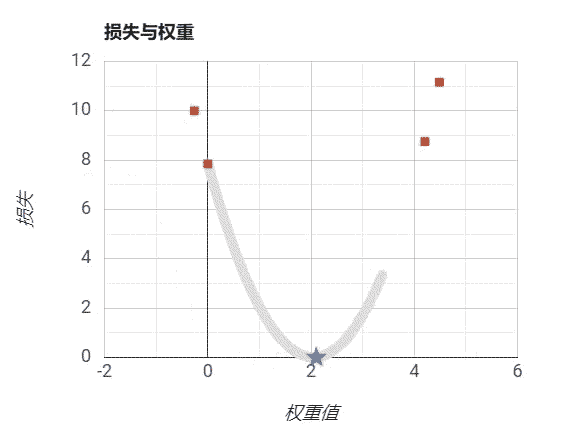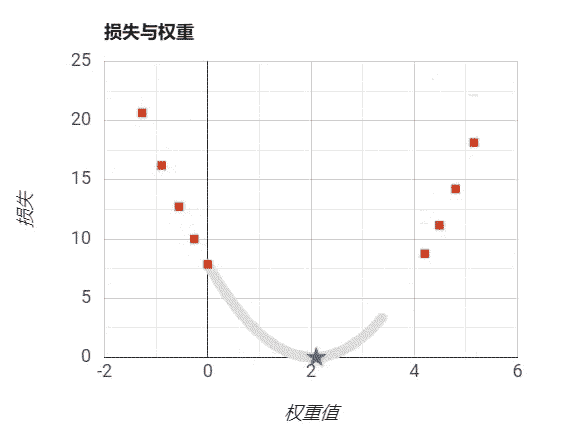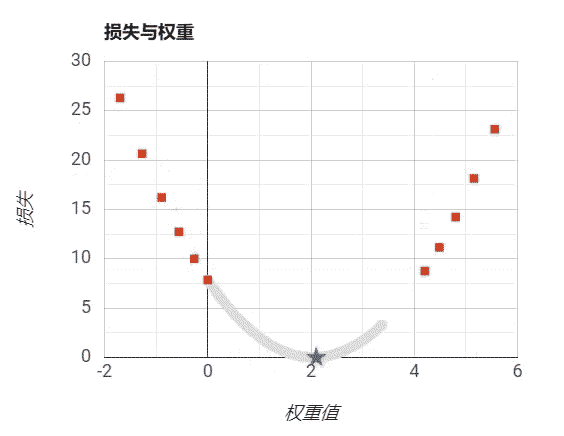
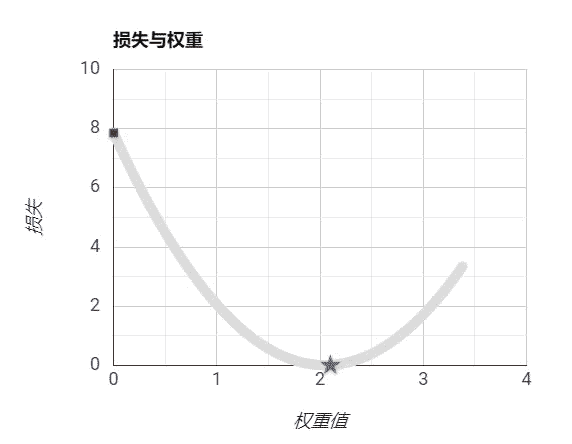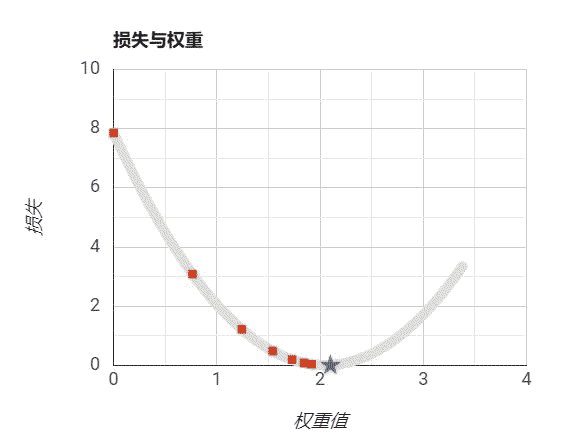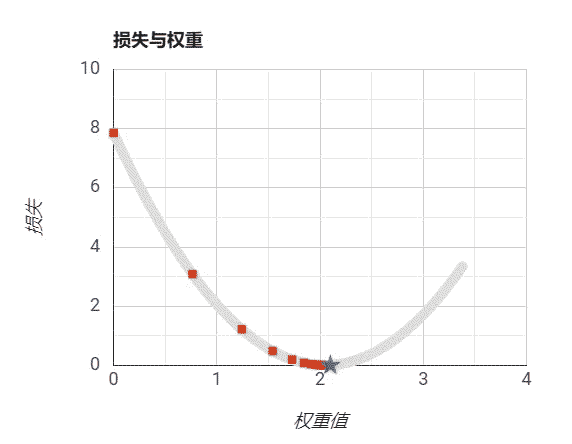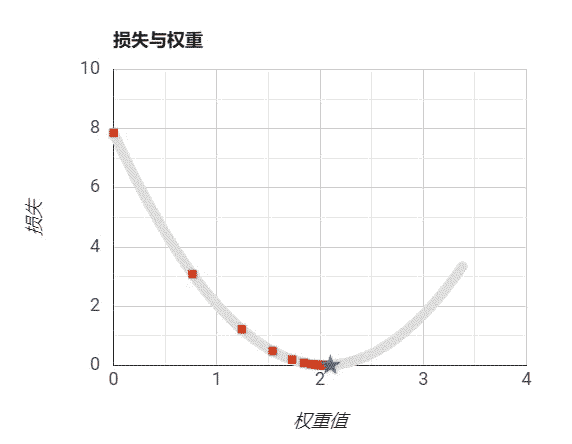
我们从-50开始到50结束设置w的值,我们通过随机数来是指偏置b,然后再带入损失函数计算我们的预测和实际值的误差损失,得到如下曲线:
需要注意的是,我们绘制的图像是根据权重和损失绘制的曲线。而我们的模型表示是一条直线。
我们可以看到,在上图中我们是可以找到极小值的,大概在5左右,此处是我们损失最小的位置,这时我们的模型最能表示数据的规律。
梯度可以完全理解为导数,梯度下降的过程就是我们不断求导的过程。
学习率(步长)
不断调整权重和偏差来来寻找损失函数最小值的过程就是我们使用梯度下降方法拟合数据寻找最佳模型的过程。那么既然我们有了解决方案,是不是该考虑如何提升效率了,我们如何快速地找到最低点?
想象一下,当你迷失在山上的浓雾之中,你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。梯度下降中的一个重要的参数就是每一步的步长(学习率),如果步长太小,算法需要经过大量迭代才会收敛,如果步长太大,你可能会直接越过山谷,导致算法发散,值越来越大。
设置步长为过小:
设置步长过大:
设置步长适当:
步长是算法自己学习不出来的,它必须由外界指定。
这种算法不能学习,需要人为设定的参数,就叫做超参数。
线性回归
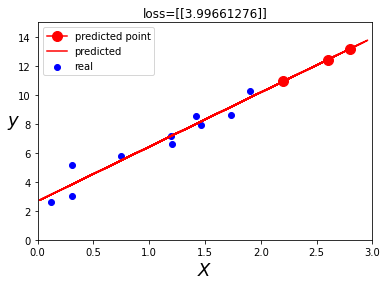
最终我们找到了线性模型来解释自变量x与因变量y之间的关系,这就是线性回归。回归的解释是,事物总是倾向于朝着某种“平均”发展,这种趋势叫做回归,所以回归多用于预测。
上图,红线是我们拟合出的最佳模型,在此模型上我们可以寻找到2.2,2.6,2.8的预测值,分别对应图中的三个红点。
这也是线性回归的基本意义。
代码实践
准备数据:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
X = 2 * np.random.rand(10)
y = 4 + 3 * X + np.random.randn(10)
plt.plot(X, y, "bo")
plt.xlabel("$X$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()绘制y=3x+2和y=4x+4两条直线:
plt.plot(X, y, "bo")
plt.plot(X, 3*X+2, "r-", lw="5", label = "y=3x+2")
plt.plot(X, 4*X+4, "g:", lw="5", label = "y=4x+4")
plt.xlabel("$X$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.legend(loc="upper left")
plt.show()计算损失,并比较y=3x+2和y=4x+4两条直线:
fig, ax_list = plt.subplots(nrows=1, ncols=2,figsize=(20,10))
ax_list[0].plot(X, y, "bo")
ax_list[0].plot(X, 3*X+2, "r-", lw="5", label = "y=3x+2")
loss = 0
for i in range(10):
ax_list[0].plot([X[i],X[i]], [y[i],3*X[i]+2], color='grey')
loss= loss + np.square(3*X[i]+2-y[i])
pass
ax_list[0].axis([0, 2, 0, 15])
ax_list[0].legend(loc="upper left")
ax_list[0].title.set_text('loss=%s'%loss)
ax_list[1].plot(X, y, "bo")
ax_list[1].plot(X, 4*X+4, "g:", lw="5", label = "y=4x+4")
loss = 0
for i in range(10):
ax_list[1].plot([X[i],X[i]], [y[i],4*X[i]+4], color='grey')
loss= loss + np.square(4*X[i]+4-y[i])
pass
ax_list[1].axis([0, 2, 0, 15])
ax_list[1].legend(loc="upper left")
ax_list[1].title.set_text('loss=%s'%loss)
fig.subplots_adjust(wspace=0.1,hspace=0.5)
fig.suptitle("Calculate loss",fontsize=16)训练模型,并预测:
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X.reshape(-1,1),y.reshape(-1,1))
X_test = [[2.2],[2.6],[2.8]]
y_test = lr.predict(X_test)
X_pred = 3 * np.random.rand(100, 1)
y_pred = lr.predict(X_pred)
plt.scatter(X,y, c='b', label='real')
plt.plot(X_test,y_test, 'r', label='predicted point' ,marker=".", ms=20)
plt.plot(X_pred,y_pred, 'r-', label='predicted')
plt.xlabel("$X$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 3, 0, 15])
plt.legend(loc="upper left")
loss = 0
for i in range(10):
loss = loss + np.square(y[i]-lr.predict([[X[i]]]))
plt.title("loss=%s"%loss)
plt.show()其他回归
要怎么真正理解回归(regression)呢?通过大量的数据统计,个体小的豆子往往倾向于产生比其更大的后代,而个体大的豆子往往倾向于产生比其更小的后代,新产生的个体有向着豆子的平均值的一种趋势,这种趋势就是回归。我们本篇文章讲的线性回归就是应用于预测的一种技术。这时,回归往往与分类相对。
线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索(Lasso)回归、弹性网络(ElasticNet)回归是最常用的回归技术。我先对这些技术做一个简单整理,让大家把脉络理清,等大家实际需要再深入探索。试图去穷尽知识只会把自己拖向疲累。
| 名称 | 解释 | 公式 |
|---|---|---|
| 线性回归(Linear Regression) | 一种以线性模型来建模自变量与因变量关系的方法 | $$ y = wx+b $$ |
| 逻辑回归(Logistic Regression) | 对特定类别进行建模,用于二分类 | $$ y=\frac{1}{1+e^{-x}} $$ |
| 多项式回归(Polynomial Regression) | 自变量 x 和因变量 y 之间的关系被建模为关于 x 的 n 次多项式 | $$ y=\beta_0 + \beta_1x + \beta_2x^2 + ... + \beta_mx^m + \varepsilon $$ (cαiyongji水印) |
| 逐步回归(Stepwise Regression) | 将多个变量一个一个地引入到模型,找到其对模型影响大的变量 | |
| 套索回归(Lasso Regression) | 稀疏矩阵,消除不重要的特征,MSE+L1范数 | $$ J(\theta)=MSE(\theta) + \alpha\sum\mid\theta\mid $$ ,其中,α越大模型权重越小 |
| 岭回归(Ridge Regression) | 正则化线性回归,增加模型自由度,防止过拟合,MSE+L2范数 | $$ J(\theta)=MSE(\theta) + \alpha\frac{1}{2}\sum\theta^2 $$ ,其中,α越大模型权重越小 |
| 弹性网络(ElasticNet) | 介于岭回归和Lasso回归之间 | $$ J(\theta)=MSE(\theta) + \gamma\alpha\sum\mid\theta\mid + \alpha\frac{1-\gamma}{2}\sum\theta^2 $$ ,其中,γ介于0和1之间,接近0则更倾向于岭回归,接近1则更倾向于Lasso回归 |