时间序列-ARIMA模型调参检验实战
文章目录
-
-
-
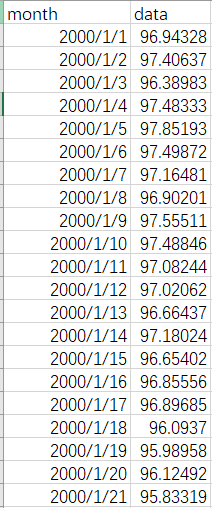
- 1.数据格式
- 2.理论补充
- 3.代码
- 4.总结
-
-
1.数据格式
2.理论补充
3.代码
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: ArmaModel(2,2)or(0,1).py
@time: 2020/11/6 17:33
"""
'''
模型的介绍:
AR、MA、ARMA、ARIMA模型 参考:https://blog.csdn.net/u010687164/article/details/86010154
1.自回归模型AR(p)模型:利用时间序列前期数值与后期数值的相关关系,建立一个包含前后期数值的自变量回归方程
2.移动平均MA(q)模型:t 时间点的序列值为白噪声 u_t 的加权之和
3.自回归滑动平滑ARMA(p,q)模型:移动平均方程是对自回归模型的一个补充.这种模型综合了AR与MA两种模型的优势,解决了随机变动项的求解问题。
4.ARIMA(p,q,d)模型:AR/MA/ARMA用于分析平稳时间序列,接下来所说的ARIMA通过差分可以用于处理非平稳时间序列。参数d为差分的次数。
相比于ARMA模型,该模型需要将不平稳数据进行d次差分形成一个稳定的时间序列数据,然后采用ARMA模型
'''
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels as sm
from datetime import datetime
# 作qq图
from statsmodels.graphics.api import qqplot
# 作ADF单方根检验
from statsmodels.tsa.stattools import adfuller as ADF
# 自相关、偏自相关
from statsmodels.tsa.stattools import acf, pacf
# ARMA模型
from statsmodels.tsa.arima_model import ARMA
# ARIMA模型
from statsmodels.tsa.arima_model import ARIMA
# 季节性分解
from statsmodels.tsa.seasonal import seasonal_decompose
# 作自相关图与偏自相关图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# SciPy的stats模块提供了大约80种连续随机变量和10多种离散分布变量
from scipy import stats
# D-W检验
from statsmodels.stats.stattools import durbin_watson
from sklearn.metrics import mean_squared_error
class ArimaModelTest:
'''
ARIMA建模的基本步骤:
1.获取被观测的时间序列数据
2.对时序数据进行平稳化处理,利用差分寻找最佳的d值
3.根据平稳化处理后的时序数据自相关、偏相关图选择合适的p,q值,并对ARIMA模型进行AIC,BIC,HQIC准则验证
4.检查残差序列:分别用自相关、偏自相关、D-W检验,正态分布检验、qq图检验、Ljung-Box检验
5.最后进行数据预测
'''
# 参数初始化
def __init__(self, lags):
self.lags = lags
# 第一步:平稳性检验
'''
时序数据平稳性是进行时间序列分析的前提条件,为什么需要满足平稳性要求呢?在大数定理与中心极限定理中要求样本同分布
(这里的同分布等价于时间序列中的平稳性),我们在建模过程中有很多是建立在大数定理与中心极限定理条件下的,如果它不满足,
得到的很多结论都不可靠
平稳性检验一般采用观察法与检验法
python判断时序数据的稳定性
有两种方法:1.Rolling statistic--即每个时间段内的数据均值与标准差情况
2.ADF单方根检验
Dickey-Fuller Test 在一定的置信水平下,对于时间序列数据假设Null hypothesis:非稳定
如果检验值小于临界值,则拒绝null hypothesis,即数据是稳定的,反之是非稳定的
查看结果参考:https://blog.csdn.net/qq_18999357/article/details/85097797
p值越小越好,p值要求小于给定的显著水平,p值要小于0.05,等于0是最好的。
'''
def test_stationarity(self, timeseries, window):
# 移动平均图
rol_mean = timeseries.rolling(window=window).mean()
rol_std = timeseries.rolling(window=window).std()
fig = plt.figure(facecolor='white')
fig.add_subplot()
plt.plot(timeseries, 'r-', label='Original')
plt.plot(rol_mean, 'b-', label='rolling_mean')
plt.plot(rol_std, 'g-', label='rolling_std')
plt.legend(loc='best')
plt.title('Rolling Mean', fontsize=20)
plt.show(block=False)
# Dickey-Fuller Test
print('Results of Dickey-Fuller Test:')
# dftest的输出前几项依次为检测值、p值、滞后数、使用的观测数、各个置信度下的临界值
dftest = ADF(timeseries, autolag='AIC')
# print(dftest)
dfoutput = pd.Series(dftest[0:4],
index=['Test Statistic', 'p-value', 'Lags Used', 'Number of Observations Used'])
# 打印各个置信度下的临界值
for key, value in dftest[4].items():
dfoutput['Critical value (%s)' % key] = value
print(dfoutput)
# 第二步:对时间序列做平稳化处理(一般使用差分)
# 数据不稳定的原因主要有两个:1.趋势-数据随着时间变化,比如升高或者降低 2.季节性-数据在特定的时间段内变动
# 检测与去除趋势,一般有三种方式:
'''
1.聚合:将时间轴缩短,以一段时间内星期、月、年的均值作为数据值,使不同时间段内的值差距缩小
2.平滑:以一个滑动窗口内的均值代替原来的值,为了使值之间的差距缩小
3.多项式过滤:用一个回归模型来拟合现有数据,使得数据更平滑
平滑一般有移动平均与指数加权移动平均
移动平均是将所有时间平等看待
指数加权平均是认为越近的时刻越重要,多了一个半衰期指定衰减
'''
# 检测与去除季节性,一般有两种方式:
'''
1.差分化:与特定滞后数目的时刻的值作差
2.分解:对趋势与季节性分别建模然后再移除它们
'''
def set_stable_plot(self, timeseries, target, diff=1):
# global关键字的作用是可以修改全局变量的值
global data
# 由于原数据值域范围比较大,为了缩小值域,同时保留其他信息,常用的方法是对数化,取log
data = np.log(timeseries)
data = data.diff(diff)
data.dropna(inplace=True)
# 第三步:选择合适的p、q,做自相关图ACF与偏自相关图PACF
'''
参考博客:https://blog.csdn.net/weixin_41013322 见判断模型表格
https://blog.csdn.net/xianyuhenxian/article/details/60602828
https://blog.csdn.net/Jasminexjf/article/details/94993362
自相关函数 (ACF):延迟为 k 时,这是相距 k 个时间间隔的序列值之间的相关性。
偏自相关函数 (PACF):延迟为 k 时,这是相距 k 个时间间隔的序列值之间的相关性,同时考虑了间隔之间的值。
截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);
拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF)。
截尾:在大于某个常数k后快速趋于0为k阶截尾
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
'''
'''
ACF图与PACF图分析:
可以看到ACF呈现1阶截尾,PACF呈现拖尾,所以选用MA(1)模型
'''
def p_q_choice(self, timeseries):
# 直接得出最优模型,同时使AIC与BIC最小
res = sm.tsa.stattools.arma_order_select_ic(timeseries, ic=['aic', 'bic', 'hqic'],trend='nc')
print('AIC:', res.aic_min_order)
print('BIC:', res.bic_min_order)
print('HQIC:', res.hqic_min_order)
fig = plt.figure(figsize=(12, 6))
ax1 = fig.add_subplot(211)
# lags表示滞后阶数
fig1 = plot_acf(timeseries, lags=self.lags, ax=ax1)
ax2 = fig.add_subplot(212)
fig2 = plot_pacf(timeseries, lags=self.lags, ax=ax2)
plt.show()
# 第四步:利用ARMA模型的AIC准则,找出最优模型
def model_eval(self, timeseries, order):
global arma_model
arma = ARMA(timeseries, order=order)
arma_model = arma.fit(disp=-1) # disp<0:不输出过程
print(u'----------ARMA模型-------------')
print('AIC:', arma_model.aic)
print('BIC:', arma_model.bic)
print('HQIC:', arma_model.hqic)
# 第五步:检查残差序列,D-W(德宾-沃夫)检验
'''
参考:https://blog.csdn.net/dingming001/article/details/73823376
https://blog.csdn.net/robert_chen1988/article/details/106158129
在考虑多元自回归的模型的残差独立性时提出的一个自相关检验统计量,我们把它借鉴过来进行时间序列的残差自相关检验
如果检验结果显示残差序列自相关性不显著,说明回归模型对信息的提取比较充分,可以停止分析。
如果检验结果显示残差序列自相关性显著,说明回归模型对信息的提取不充分,可以考虑对残差序列拟合自回归模型。
这样的模型叫做残差自回归模型。
D-W: 2.0146543495411566
该统计量值越接近 2 越好,一般在 1~3 之间说明没问题,小于 1 这说明残差存在自相关性(有临界值表可以查)
'''
def check_rasid_DW(self):
dw = durbin_watson(arma_model.resid.values)
print('D-W:', dw)
# 第六步:对残差做正态分布检验
def check_normal_qq(self):
# normaltest用于做正态分布检验
# 输出结果中第一个为统计量,第二个为P值(注:p值大于显著性水平0.05,认为样本数据符合正态分布
norm = stats.normaltest(arma_model.resid)
print('normal:', norm)
fig = plt.figure()
ax = fig.add_subplot(111)
# 如果fit为真,则用dist分布自动拟合dist的参数。由标准化的数据减去拟合的loc,再除以拟合的scale,得到分位数。
# line=’q‘表示一条线适合通过四分位
figqq = qqplot(arma_model.resid, ax=ax, fit=True, line='q')
plt.show()
# 第七步:残差Ljung-Box检验(Q检验)-白噪声检验
'''
参考:https://robjhyndman.com/hyndsight/ljung-box-test/
当p-value<0.05(一般都用1%, 5%, 10%), 拒绝原假设H0,结果显著,序列相关;
当p-value>0.05,接受原假设H0,结果不显著,序列不相关,认为是白噪序列。
如何判定滞后lag——m值?
当数据没有季节性,那么我们lag就取10 【Box.test(data,lag=10)】,
当数据有季节性,那么lag就取period的2倍
'''
def check_q(self):
# 利用squeeze()函数将表示向量的数组转换为秩为1的数组即Series格式
# qstat=True含义:如果为真,返回每个自相关系数的Ljung-Box q统计量
r, q, p = acf(arma_model.resid.squeeze(), qstat=True)
data1 = np.c_[range(1, 41), r[1:], q, p]
frame = pd.DataFrame(data1, columns=['Lags', 'AC', 'Q', 'Prob(>Q)'])
frame = frame.set_index('Lags')
pct = len(frame[frame['Prob(>Q)'] > 0.05]) / len(frame)
print(frame)
print('pct:', pct)
# 第八步:平稳模型预测
def predict_target(self):
# 切分数据集,测试集大小设置为100
test_size = 100
rolling_size = 120
value = np.log(data1['data'][-test_size])
test = data[-test_size:]
pre = [] # 用来存放预测值
for i in range(len(test)):
if i % 20 ==0:
print(i)
train = data[-(test_size + rolling_size - i):-(test_size - i)]
model = ARMA(train,order=order)
model_fit = model.fit(disp=-1)
forecast = model_fit.forecast()[0]
# print(forecast)
pre.append(forecast)
return pre,value
# 第九步:将预测值还原到原来的形式,并计算RMSE
def restore_style_plot(self, predict=None, values = None):
# 还原
test = data1[-100:]
predict = pd.Series(predict,index=test.index)
# 累加diff,即变成与第一个月的差分
predict_cumsum = predict.cumsum()
predict_value = pd.Series(value,index=test.index)
predict_log = predict_value.add(predict_cumsum,fill_value = 0)
predict_original = predict_log.apply(lambda x : np.exp(x))
print('predict_original:\n',predict_original)
# rmse
rmse = np.sqrt(mean_squared_error(predict_original,test))
# 作图对比
fig = plt.figure()
fig.add_subplot(111)
plt.plot(test, 'r-', label='test_Oringial')
plt.plot(predict_original[:100], 'b-', label='predictions')
plt.legend(loc='best')
plt.title('RMSE : %.4f'%rmse)
plt.show()
if __name__ == '__main__':
warnings.filterwarnings(action='ignore')
# 1.利用pandas获取时序数据,并进行处理
# pd.read_csv(filepath,sep,header,index_col,squeeze,parse_dates,date_parser,encoding)
# 常用参数含义
'''
filepath:文件名
sep:分隔符,默认’,‘
header:用作列名的行号,一般header=0
index_col:作为DataFrame的行标签的列,以字符串名称或列索引的形式给出。如果给定一个int / str序列,则使用一个多索引;index_col=False可以用来强制panda不使用第一列作为索引
squeeze:默认False,如果解析后的数据只包含一列,则返回一个Series。
parse_dates:数据格式为bool或列表,把某一列或某几列解析为时间索引;对于非标准日期时间解析,在pd.read_csv()后使用pd.to_datetime()
date_parser:函数,用于将字符串列序列转换为日期时间实例数组
encoding:编码格式
'''
# 返回:以逗号分隔的值(csv)文件被返回为带有标记轴的二维数据结构(DataFrame)
date_parser = lambda dates: datetime.strptime(dates, '%Y/%m/%d')
data1 = pd.read_csv('../data/Data.csv', header=0, parse_dates=['month'], date_parser=date_parser, index_col='month')
# 将DataFrame对象转变成Series对象
data = data1['data']
arima = ArimaModelTest(lags=40)
# 对原数据进行平稳性检验
arima.test_stationarity(data,window=30)
# 对原数据做平稳化处理,比较一阶差分与二阶差分效果,找出最适合的差分次数d
arima.set_stable_plot(data, target='data', diff=1)
# arima.set_stable_plot(data,target='data',diff=2)
# 对处理后的数据进行平稳化检验
arima.test_stationarity(data, window=30)
# 通过自相关图与偏自相关图找到ARIMA模型中合适p、q
arima.p_q_choice(data)
# 拟合,找出最佳模型,
# 这里直接调用sm.tsa.stattools.arma_order_select_ic,并利用aic_min_order属性得出最优模型是(2,2)
order = (2, 2) # (0,1)
arima.model_eval(data, order=order)
# 检查残差序列,D-W(德宾-沃夫)检验
arima.check_rasid_DW()
# D-W: 2.0146543495411566,结果表明不存在自相关性
# 观察是否符合正态分布,这里用qq图
arima.check_normal_qq()
# 结果表明残差值不符合正态分布
# Ljung-Box检验
arima.check_q()
# pct: 1.0表明p-value>0.05,接受原假设H0,结果不显著,序列不相关,认为是白噪序列
# 平稳模型预测-对未来100天进行预测
predict,value = arima.predict_target()
# print(predict)
# 将预测值还原到原始格式
arima.restore_style_plot(predict=predict,values = value)
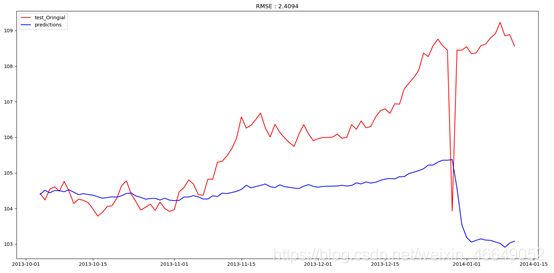
4.总结
效果没有auto-arima那么好,原因没找到,害
下一节,BP网络做神经预测,敬请期待!!!