6、集合算法

关于集成算法的参考
集成算法Python实现包：ML-Ensemble

1. 集成学习框架可分为三种：
   Bagging和Boosting都是由基函数线性组合而成。Bagging中的基函数最好是强学习器（多次有放回抽样，总体方差是基函数方差的1/N），否则可能导致整体模型的准确度低。Boosting可以是弱学习器。

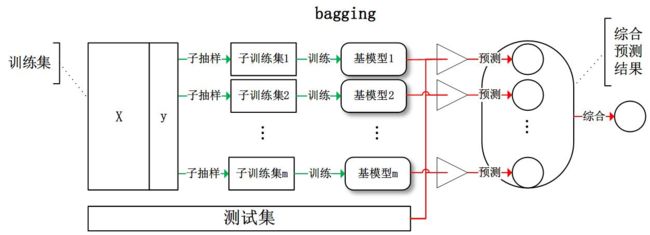
• Bagging从训练集中通过随机采样形成每个基模型所需要的子训练集，各模型之间没有关系，对所有基模型预测的结果进行综合（平均或者投票，有hard votiong和soft voting之分）产生最终的预测结果。
  
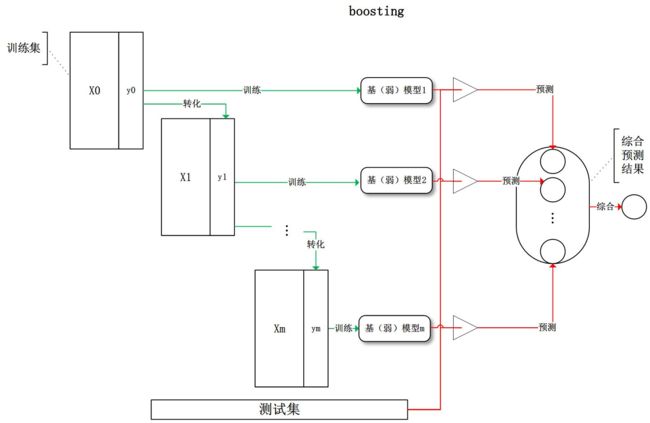
• Boosting训练过程为阶梯状，基模型按次序一一进行训练（实现上可以做到并行），基模型的训练集按照某种策略每次都进行一定的转化。对所有基模型预测的结果进行线性综合产生最终的预测结果。
• • Adaboosting：对同样数据集，每次训练模型后，根据预测结果对样本权重进行调整（提高错误样本权重，降低正确样本权重），然后继续对该批数据进行模型训练；最后将各模型的结果进行综合就是最终结果。
• • Gradient Boosting：对一批数据进行训练后，对残差再进行训练建立新模型，以此类推，最终结果是各基模型的和。
    
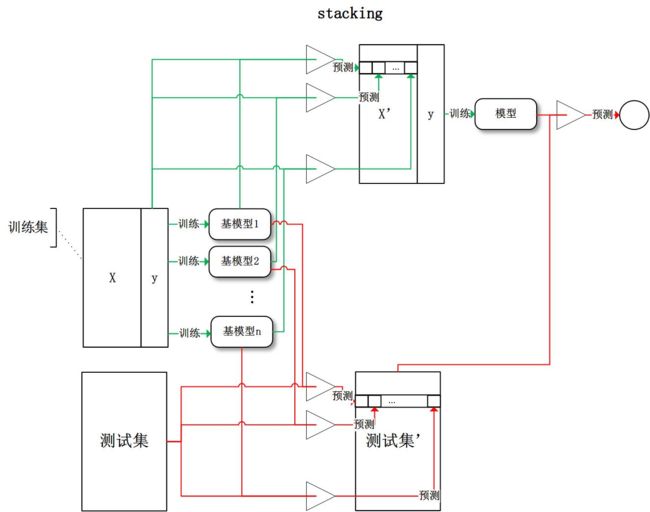
• Stacking：将训练好的所有基模型对训练集进行预测，第$j$个基模型以第$i$个训练样本的预测值将作为其训练集中的第$i$个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测
  

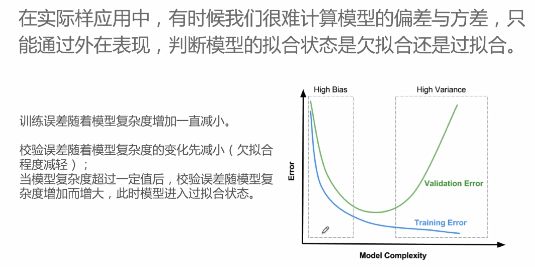
2. 偏差和方差
   偏差是预测值和真实值之间的差异，体现在训练集的准确度上；方差是预测值作为随机变量时预测结果的离散程度，体现在测试集的准确度上，方差大时容易过拟合。通过集合众多弱学习器来解决高偏差问题，基函数最好是低方差高偏差的。
   
   

一、Bagging

Bagging集成算法是Bootstrap Aggregating的缩写，对数据集通过有放回的随机采样建多个模型，各模型之间没有关系；对所有基模型预测的结果进行综合产生最终的预测结果，常用算数平均或最多票数的种类。对弱学习器没有限制，但常用的是决策树和神经网络。
随机采样(bootsrap)是从训练集里用有放回的方式抽取固定个数的样本，之前采集到的样本在放回后仍可能被抽到。
通常随机抽样后的形成的新样本集合大小和原数据集大小相同。若有$m$个样本，则每次抽中概率为$\frac{1}{m}$，在$m$次采样中都为被抽取到的概率是$(1-\frac{1}{m}{)}^m$，从而有$(1-\frac{1}{m}{)}^m\to \frac{1}{e}\simeq 0.368$，即有约36.8%的样本会始终无法被采集。这部分样本成为袋外样本（Out Of Bag，OOB），通常用于检测模型泛化能力。
Bagging算法由于每次都用随机抽样来训练模型，因此泛化能力强，方差小，但由于未使用全部数据，偏差会大。

随机森林（Random Forest，RF）

随机森林建立在Bagging的基础上，用CART决策树作为弱学习器，对样本进行有放回的随机抽样（同原数据集大小），大小和元数据集相同；再对每个决策树的特征进行随机筛选（是在根节点，不再是全部特征；也可以理解为在节点划分上随机从特征中抽取选择最优划分特征）;建每颗树时的有放回样本抽样会有约1/3样本无法被抽到，可用于做袋外估计（OOB，outofbag）来评估性能；最终一个样本的预测结果由各树进行投票或平均。
RandomForest只能接受数值型变量，对于分类变量，需要进行如One-Hot编码的转换。
【重点参数】各树间的相关性与决策树所用特征量有关，特征越多，相关性可能越强；减少使用的特征个数，树的相关性和分类能力都会降低。
【有放回抽样原因】每颗决策树都用完全不同的数据来构建，则每棵树都是“片面”的，缺少共性，对最终的汇总结果没有帮助。
【袋外估计】效果与K折交叉验证相似。
【优点】：可以给出各特征对于输出的重要性矩阵；产生的模型方差小，泛化能力强；采用袋外估计，无需进行K折交叉验证；可以并行计算，速度快；对缺失值不敏感。
【缺点】：对噪音较大的样本集容易过拟合；值比较多的特征容易对模型产生影响。
【特征重要性】判断每个特征在随机森林的每颗树上做了多大的贡献，然后取平均值即可。其中关于贡献的计算方式有：

1. 基于基尼指数变化量：该特征在所有树中的变化和$VI{M}_j={\sum }_{j\_tree}({\sum }_{i\_node}(G_{before\_split}-G_{left\_node}-G_{right\_node}))$，之后再做归一化即可$\frac{VI{M}_j}{\sum VI{M}_j}$
2. 基于袋外数据错误率：对于一树用OOB样本得到误差$e_1$；然后随机改变OOB中的第$j$列中样本的顺序，并保持其他列不变，得到新的误差$e_2$。通过$e_1-e_2$ 来刻画特征$j$的重要性。依据是，如果一个特征很重要，那么其变动后会非常影响测试误差，如果测试误差没有怎么改变，则说明特征$j$不重要。

打乱特征j的样本顺序由两种方法：
1）是使用均匀分布或者正态分布随机值来抽样替换原特征；
2）是通过permutation test（随机排序测试、置换检验）将原来的所有N个样本的第$j$个特征值重新打乱分布（相当于重新洗牌），保证了特征替代值与原特征的分布是近似的（只是重新洗牌而已）。参考

4. 经过结点的数目等指。可以算出每个特征平均减少了多少不纯度，并把它平均减少的不纯度作为特征选择的标准。随机森林基于不纯度的排序结果非常鲜明，在得分最高的几个特征之后的特征，得分急剧的下降。参考
   随机森林的变种还有Extra Trees（每个决策树都用原始训练集，不抽样；选用随机特征值划分决策树）
   随机森林的基评估器都拥有较低的偏差和较高的方差，因为决策树本身是预测比较”准“，比较容易过拟合的模型，装袋法本身也要求基分类器的准确率必须要有50%以上。所以以随机森林为代表的装袋法的训练过程旨在降低方差，即降低模型复杂度。

Extra Trees

Extra trees是基于随机森林，但样本使用原始训练集，在特征划分时随机选择特征并随机选择划分阈值进行划分（不再使用具体准则）。
极大的抑制了过拟合，但增加了拟合的偏差

Totally Random Trees Embedding

简称TRTE，是一种无监督的将低维的数据集映射到高维的方法，从而让映射到高维的数据可以更好的用于分类或回归。
TRTE在数据转化的过程用了类似于RF的方法，建立T个决策树来拟合数据。当决策树建立完毕后，数据集里的每个数据在T个决策树中叶节点的位置也定下来了。从而将样本在每颗决策树中用one-hot（在对应节点为1，不在为0）编码表示的结果按树的顺序合在一起，映射结果维度$n_{o}ut\le Node\ast Tree$。实际上是实现了高维离散化。
示例：有3颗决策树，每个决策树有5个叶子节点，某个数据特征x划分到第一个决策树的第2个叶子节点，第二个决策树的第3个叶子节点，第三个决策树的第5个叶子节点。则x映射后的特征编码为(0,1,0,0,0, 0,0,1,0,0, 0,0,0,0,1)，有15维的高维特征。这里特征维度之间加上空格是为了强调三颗决策树各自的子编码。映射到高维特征后，可以继续使用监督学习的各种分类回归算法了。

Isolation Forest

简称IForest，是一种异常点监测方法。
随机采样时，所采子样本量远远小于原始训练集个数（通过部分数据来区分异常点）。每次建立决策树时，随机选择一个划分特征，并随机选择划分阈值。通过较小的决策树深度进行建模（少量异常点检测一般不用大规模树）。
对于异常点的判断是，将测试样本点$x$用T颗树进行拟合，计算每颗决策树上该样本点所在的叶节点对应的深度$h_t(x)$，从而可计算平均高度${\overline{h}}_t(x)$。
样本点$x$对应的异常概率为：$s(x,m)=2^{-\frac{\overline{h}(x)}{c(m)}}$，其中$m$是训练样本个数，$c(m)=2ln(m-1)+\xi -2\frac{m-1}{m}$，$\xi$是欧拉常数。
$s(x,m)$的取值范围是[0,1]，取值越接近1，则$x$是异常点的概率越大。

多输出任务

多输出任务是对一个输入样本会输出多个目标值（多个y，不是y的多个值）。以回归为例，对单输出任务是求解$\theta$使得$X\theta =Y$，二多输出任务是求解$\theta =({\theta }_1,{\theta }_2)$使得$X({\theta }_1,{\theta }_2)=(Y_1,Y_2)$。对多输出任务，若各输出间相互独立，则多输出效果同多个单输出任务效果相似；但若各输出间有关联，则结果会不同与单输出任务的组合。

参考：https://www.cnblogs.com/pinard/p/6156009.html

二、Boosting（提升）

【工作机制】首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重。使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2。如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。　

Boosting面临四个问题：

1. 如何计算学习误差率$e$?
2. 如何得到弱学习器权重系数$\alpha$?
3. 如何更新样本权重向量$D$?
4. 使用何种结合策略？

AdaBoost算法

AdaBoost非常好的参考
AdaBoost算法（Adaptive Boost）可用于分类数据（二分类），对多分类任务，需要将任务通过OvR（一对多）转换成二分类任务；也可以用于回归。
AdaBoost每次都用全部数据，主要通过调整样本权重来建立各次迭代时的弱学习器。能够在学习过程中不断减少训练误差，且训练误差是以指数速度下降的。由于重视误分类样本的权重，因此对异常样本敏感，影响最终的强学习器的预测准确性。
AdaBoost算法可以认为是加法模型（弱学习器的线性组合）、损失函数为指数函数、学习算法为前向分布算法时的学习方法。

AdaBoost分类算法（自适应提升算法）

【思路】初始化时给数据集每个样本一个权重，用带权重的数据集来训练弱学习器。训练出模型后，针对这个模型中预测错误的样本，增加其权重值；对预测正确的样本，减少其权重。再根据计算出的误差给弱学习器一个权重。然后用新的样本权重调整后的样本继续训练新的弱学习器，重复得到B个模型。最后将B个弱学习器用对应的权重加总作为整体的强学习器。各弱学习器间相互依赖（样本权重受上一模型影响）。整个学习过程中使用的都是同一批样本，只是调整样本权重。
【过程】输入：训练集$T=\{(x_{,}{y}_1),(x_2,y_2),...(x_m,y_m)\}$；分类y={-1,+1}

1. 初始化训练集的权值分布：$D(1)=(w_{1,1},w_{1,2},...w_{1,m});w_{1,i}=\frac{1}{m};i=1,2...m$
2. 对$k=1、2、\dots M$
   a) 使用有权值分布$D(k)$的训练集学习得到分类器$G_k(x)$（输出0/1）
   b) 计算$G_k(x)$在训练集上的分类误差率：$e_k=\sum P(G_k(x_i)\ne y_i)=\sum w_{k,i}I(G_k(x_i)\ne y_i)$（$I(G_k(x_i)\ne y_i)$是指示函数，与实际类不相同时取1，相同时取0。分类误差率是与实际类别不同的样本的权值和）
   c) 计算$G_k(x)$的系数${\alpha }_m=\frac{1}{2}log\frac{1-e_k}{e_k}$，表示基本分类器$G_m(x)$的重要性。误差越小$\alpha$值越大：$e_k>0.5时\alpha <0$；$e_k<0.5时\alpha >0$。
   d) 更新数据集的权值分布：$D(k+1)=(w_{k+1,1},w_{k+1,2},...w_{k+1,m})$，
   其中$w_{k+1,i}=\frac{w_{k,i}}{Z_k}{e}^{-{\alpha }_k{y}_i{G}_k(x_i)}$， $Z_k=\sum w_{k,i}{e}^{-{\alpha }_k{y}_i{G}_k(x_i)}$
   实际就是分别改变误分类样本和正确分类样本的权重，使正确分类的权值减小，错误分类的权值变大。
3. 构建基本分类器的线性组合：$f(x)=\sum {\alpha }_k{G}_k(x)=f_{k-1}(x)+{\alpha }_k{G}_k(x)$。$f(x)>0时\hat{y}=1$；$f(x)<0时\hat{y}=0$。$f(x)$值大小反映对应类的预测置信度。
   也可以对弱学习器添加正则项（学习步长）：$f_k(x)=f_{k-1}(x)+\nu {\alpha }_k{G}_k(x)$，$0<\nu \le 1$。
4. 到达指定迭代次数（还可以对树进行限制）或分类误差率达到一定值后停止迭代，得到最终的分类器：$G(x)=sign(f(x))=sign(\sum {\alpha }_k{G}_k(x))$

【Adaboost是前向分步学习算法】对第k轮迭代：$f_k(x)=f_{k-1}(x)+{\alpha }_k{G}_k(x)$
【损失函数为指数函数】定义总体损失函数$\underset{\alpha ,G}{argmin}\sum _{i=1}^{m}exp(-y_i{f}_k(x))$
利用前向分步学习算法的关系可以得到损失函数为$({\alpha }_k,G_k(x))=\underset{\alpha ,G}{argmin}\sum _{i=1}^{m}exp[(-y_i)(f_{k-1}(x)+{\alpha }_k{G}_k(x))]$
令$w_{ki}^{{}^{\prime }}=exp(-y_i{f}_{k-1}(x))$，它的值不依赖于$\alpha ,G$，是上一轮中确定的结果，仅仅依赖于$f_{k-1}(x)$，随着每一轮迭代而改变，与本轮最小化时所求$G_k$无关。从而有$({\alpha }_k,G_k(x))=\underset{\alpha ,G}{argmin}\sum _{i=1}^m{w}_{ki}^{{}^{\prime }}exp[-y_i{\alpha }_k{G}_k(x)]$。
又由于$G_k(x)=\underset{G}{argmin}\sum _{i=1}^m{w}_{ki}^{{}^{\prime }}I(y_i\ne G(x_i))$，从而带入损失函数，对$\alpha$求导并使其为0，可得：${\alpha }_k=\frac{1}{2}log\frac{1-e_k}{e_k}$
$e_k$即为我们前面的分类误差率：$e_k=\frac{\sum _{i=1}^m{w}_{ki}^{’}I(y_i\ne G(x_i))}{\sum _{i=1}^m{w}_{ki}^{’}}=\sum _{i=1}^m{w}_{ki}I(y_i\ne G(x_i))$
【何时停止建树？？】

Adaboost回归算法

对于第$k$个弱学习器，总体最大误差：$E_k=max|y_i-G_k(x_i)|i=1,2...m$
对每个样本的误差根据不同定义可以有：若为线性误差，则$e_{ki}=\frac{|y_i-G_k(x_i)|}{E_k}$；若为平方误差，则时$e_{ki}=\frac{(y_i-G_k(x_i){)}^2}{E_k^2}$；若为指数误差，则$e_{ki}=1-exp(\frac{-y_i+G_k(x_i))}{E_k})$。
最终得到第k个弱学习器的误差率：$e_k=\sum _{i=1}^m{w}_{ki}{e}_{ki}$
第k个弱学习器的样本$i$的权重${\alpha }_{k,i}=\frac{e_{k,i}}{1-e_{k,i}}$，则第$k+1$个弱学习器的样本集权重系数为$w_{k+1,i}=\frac{w_{ki}}{Z_k}{\alpha }_k^{1-e_{ki}}$，其中$Z_k=\sum _{i=1}^m{w}_{ki}{\alpha }_k^{1-e_{ki}}$。
弱学习器的结合策略是对加权的弱学习器，取权重倒数的对数的中位数对应的弱学习器作为强学习器，最终的强回归器为$f(x)=G_{k^{\ast }}(x)$，$G_{k^{\ast }}(x)$是$ln\frac{1}{{\alpha }_k},k=1,2,....K$的中位数值对应序号$k^{\ast }$对应的弱学习器。

梯度提升Gradient boosting

一、理论推导

梯度提升算法是以基函数为变量求解损失函数最小化，基于加法模型，利用前向分布算法，根据泰勒一阶展开式得出基函数尽可能拟合上一模型的负梯度时，能够使损失函数最小化，实现逐渐逼近总体损失函数的局部最优值。
称为Gradient是因为在添加新模型时用了梯度下降算法来实现损失函数最小化。
【加法模型】$F(x)=\sum {\beta }_m{f}_m(x)$
【前向分布算法】$F_t(x)=F_{t-1}(x)+{\beta }_t{f}_t(x)$
【损失函数】总体模型的损失函数：$L(y,F(x))={\sum }^{N}L(y_i,{\sum }^m{\beta }_m{f}_m(x_i))$
【泰勒一阶展开式】$f(x+\Delta x)=f(x)+\Delta f^{\prime }(x)$
【梯度下降】由于损失$L(y,F(x))={\sum }^{N}L(y_i,{\sum }^m{\beta }_t{f}_t(x_i))=\sum L(y_i,F_{t-1}(x_i)+{\beta }_t{f}_t(x_i))$是关于$F(x)$的函数，对与每个样本，根据一阶泰勒展开式可得$L(y_i,F_{t-1}(x_i)+{\beta }_t{f}_t(x_i))\approx F_{t-1}(x_i)+{\beta }_t{f}_t(x_i)\frac{L(y_i,F_{t-1}(x_i))}{F_{t-1}(x_i)}$。由于${\beta }_t>0$，从而根据梯度下降知识可知，当$f_t(x_i)=-\frac{L(y_i,F_{t-1}(x_i))}{F_{t-1}(x_i)}$（梯度下降）时有（平方项大于0），$L(y_i,F_{t-1}(x_i))\ge L(y_i,F_t(x_i))$。此时可成功降低每个样本点上的预测损失。从而有$F_t(x)=F_{t-1}(x)+f_t(x)$。参考，非常好的参考
以上是基于损失函数对总体模型$F(x)$可导的，但$F(x)$是否关于x可导不一定（即$f(x)$是否对x可导）。
对于${\beta }_t$可以通过以为搜索找到：${\beta }_t=argmi{n}_{\beta }\sum L(y_i,h_{t-1}(x_i)+\beta f_t(x_i))$。
对初始的$f_0(x)$，可以用常量，如均值等。
对于不同的基函数、不同的损失函数，都可以用上述解法来做。当损失函数为$L(F)=(y-F{)}^2$时， 对$F$的导数（不是对x求导）是$2(y-F)$，这就是残差，从而新的函数$f_m(x)$对伪残差的最大拟合实际就是对上轮迭代所得残差的最大拟合。若损失函数为其他函数时未必。
如此迭代不断找到新的$f(x)$使总体损失函数变小，此方法即为梯度提升。

【推导方法二】
若$L$关于$F$二阶可导，还可以从极值角度考虑，令$L^{\prime }=0$，而$L^{\prime }$可用泰勒展开式进行展开，从而可以计算出$f_m$的具体形式参考：

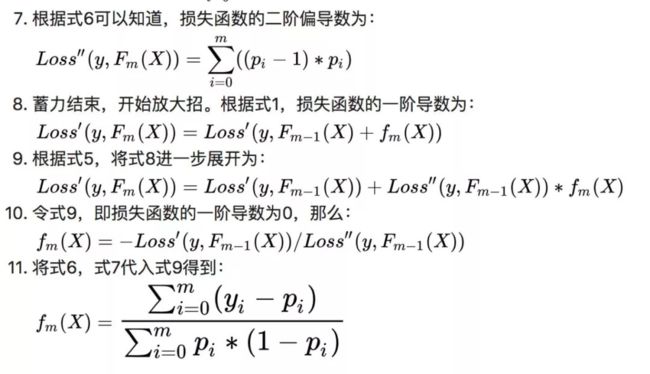
二、损失函数和梯度

【回归任务】
均方误差损失函数$L(y_m,F_m(x))=\frac{1}{2}(y-F_m(x){)}^2$此时梯度就是残差$y-F(x)$。
绝对损失函数$L(y,F(x))=|y-F(x)|$，梯度是$sign(y-F(x))$。
【分类任务】
二分类任务用逻辑回归的损失函数（logistic loss）：$L(y,F(x))=ylogp+(1-y)log(1-p)$，其中$p=\frac{1}{1+e^{-F(x)}}$，梯度是$y-\frac{1}{1+e^{-F_{m-1}(x)}}$。
多分类任务使用Sofmax的损失函数。
指数损失函数$L(y_m,F_m(x))=e^{(-y\ast F_m(x))}$。当损失函数为指数函数式，梯度提升算法相当于二分类的Adaboost算法参考
【示例】以逻辑回归为例，对每个类，预测其概率时，形成${\hat{y}}^{(i)}=(p_1,p_2,p_n)$，对实际所属类可视为概率1，其余为0，如$y^{(i)}=(1,0,0)$，从而可以计算${\hat{y}}^{(i)}$与$y^{(i)}$间的距离，从而构造$f(x)$的损失函数并计算伪残差，之后再对该伪残差继续用逻辑回归建模，理论上直到所有残差为零时（或达到阈值）停止。分类的损失函数可以是预测类与真实类不一致的数量、叶节点的熵按叶节点占总体样本的比重做加权后的值……。

三、优化方法

【正则化】在使用提升方法时，通常会在模型权值基础上再增加一个学习率$v$（衰减因子Shrinkage），将上轮迭代的结果以一定比例缩减，削弱每个基函数的影响，让后面有更大的学习空间：$F_t(x)=F_{t-1}(x)+v\cdot {\beta }_t{f}_t(x)$。一般会把学习率设置得小一点（$v<0.1$），然后迭代次数设置得大一点。
另外在每次迭代时对样本可以进行随机无放回抽样，从而增加模型随机性，减小方差，即随机梯度提升SGD方法。

梯度提升树GBDT（Gradient Boosting Decision Tree）

参考1 参考2 很好的参考
【特点】梯度提升树是基函数为CART回归树的梯度提升法的应用。GBDT的核心在于每次对上轮所得总体模型的负梯度进行拟合（损失函数是均方误差时就是对上轮残差进行拟合），通过累加所有树的结果作为最终结果（分类树的结果无法累加，故GBDT中的树都是回归树）。虽然调整后可用于分类任务（通过基函数返回概率），但基函数不是分类学习器。最终结果是对各树结果的加权求和得到总体结果
GBDT主要由三个概念组成：Regression Decistion Tree（即DT)，Gradient Boosting（即GB)，Shrinkage (算法的一个重要演进分枝，目前大部分源码都按该版本实现）
【基函数】最好是低方差和高偏差的，从而可以通过多次迭代减小偏差。
CART决策树不用很深，可接受单个基函数的高偏差，通过集合来减小偏差。

【损失函数】GBDT可以用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
【A、分类算法常用损失函数】：

1. 指数损失函数$L(y,f(x))=exp(-yf(x))$，其负梯度计算和叶节点的最佳负梯度拟合参见Adaboost。
2. 对数损失函数，分为二元分类和多元分类两种。

B、回归算法常用损失函数】：

1. 均方差$L(y,f(x))=(y-f(x){)}^2$
2. 绝对损失$L(y,f(x))=|y-f(x)|$，对应负梯度为：$sign(y_i-f(x_i))$
3. Huber损失，是均方差和绝对损失的折衷产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下：$L(y,f(x))=\{\begin{array}{ll}\frac{1}{2}(y-f(x){)}^2& |y-f(x)|\le \delta \\ \delta (|y-f(x)|-\frac{\delta }{2})& |y-f(x)|>\delta \end{array}$。对应负梯度误差是：$r(y_i,f(x_i))=\{\begin{array}{ll}{y}_i-f(x_i)& |y_i-f(x_i)|\le \delta \\ \delta sign(y_i-f(x_i))& |y_i-f(x_i)|>\delta \end{array}$
4. 分位数损失函数，对应的是分位数回归的损失函数：$L(y,f(x))=\sum _{y\ge f(x)}\theta |y-f(x)|+\sum _{y<f(x)}(1-\theta )|y-f(x)|$,　其中$\theta$为分位数，需要我们在回归前指定。对应的负梯度误差为：$r(y_i,f(x_i))=\{\begin{array}{ll}\theta & y_i\ge f(x_i)\\ \theta -1& y_i<f(x_i)\end{array}$
   对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。

【正则化】：

1. 一种是对弱学习器添加学习率。
2. 第二种正则化的方式是通过子采样比例（subsample）。取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。
   使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。通过自采样的SGBT可以达到部分并行
3. 第三种是对于弱学习器即CART回归树进行正则化剪枝。

GBDT回归算法

每次随机无放回抽样建立CART决策树，总体损失函数用均方差（决策树的损失函数依赖于决策树）。对第$t$轮迭代，有上一次迭代的残差（伪残差）$r_{t-1,i}$。参考 过程示例

1. 利用$(x_i,r_{t-1,i})(i=1,2,..n)$拟合一颗CART回归树，对应的叶节点区域$R_{tj},j=1,2,...,J$，其中$J$为叶节点的个数。每一个叶结点的样本都可以使CART回归决策树的损失函数最小（拟合叶子节点中的残差最好），叶节点的输出值$b_{mj}$如下：
   $b_{tj}=\underset{b}{argmin}\sum _{x_i\in R_{tj}}L(y_i,f_{t-1}(x_i)+b)$。即用标签（上轮的残差或梯度值）的平均值表示该叶子节点拟合到的值：$b_{tj}=av{e}_{x_i\in R_{mj}}{r}_{t-1,i}$。
2. 得到本轮的决策树拟合函数如下：$h_t(x)=\sum _{j=1}^J{b}_{tj}I(x\in R_{tj})$。
   从而本轮得到的强学习器：$F_t(x)=F_{t-1}(x)+{\gamma }_t{f}_t(x)=F_{t-1}(x)+{\sum }_{j=1}^J{b}_{tj}I(xϵR_{tj})$
   $b_{tj}$可以看作是基于损失函数$L$的每个叶子节点的最理想的常数更新值，也可以认为是既有下降方向，又有下降步长的值。

树的建立依赖于树模型自身（如用基尼指数作为分割准则），之后获得伪残差才是关键。
【问题】具体如何确定各树的权重

GBDT分类算法：二分类

过程同GBDT回归算法，但使用损失函数不同：用指数损失函数，则GBDT退化为Adaboost算法；用对数似然损失函数，类似逻辑回归，可得到预测概率值。参考
A）以对数似然损失函数logloss作为损失函数为例：$y\in \{0,1\}$好示例参考 参考

1. 选取对数似然函数为损失函数：
   $L\left(y_i,F_m(x_i)\right)=-ln(p_i^{y_i}(1-p_i{)}^{(1-y_i)})=-(y_{i}log{p}_i+(1-y_i)log(1-p_i))$，其中$p_i=\frac{1}{1+e^{-F(x_i)}}$是标签为1的概率。将$p_i$带入可得$L\left(y_i,F_m(x_i)\right)=-(y_i{F}_m(x_i)-log(1+e^{F_m(x_i)}))$。$F(x_i)=log(\frac{p_i}{1-p_i})$
2. 初始化：$F_0(x)=log\left(\frac{{\sum }_{i=1}^N{y}_i}{{\sum }_{i=1}^N(1-y_i)}\right)$，以样本中标签为1类的样本与标签为0类的样本量之比的对数（对数几率）作为$F_0(x)$的初始值（第一次预测）。
   $F(x)$就是模型最终输出的连续值，是样本$x$经过所建立的多棵树后，在每棵树中对应叶节点的梯度的累加。$F(x)$可看做是逻辑回归中的$f(x)=w^{T}x$。将最终输出$F(x)$通过Sigmod函数可转换为对应的概率。通过不断拟合F来得到更好的p，从而获得与真实概率（0/1）最接近的预测概率p。
3. 在第$m$轮（$m\ge 1$）迭代中， 损失函数$L$所对应的负梯度为：$r_i=-{\left[\frac{\partial L(y_i,F({\mathbf{x}}_i))}{\partial F({\mathbf{x}}_i)}\right]}_{F(x)=F_{m-1}(x)}=y_i-\frac{1}{1+e^{-F_{m-1}(x_i)}}=y_i-{\hat{p}}_i$，$y_i$是标签为1对应的概率0/1。每次拟合的相当于是$w^{T}x$部分的残差，可转化为剩余的概率（预测为1）。
4. 令对数似然函数对$F_0(x)$求导后的梯度$r_0$为零，可求解出最优解的$F_0(x)=log\left(\frac{{\sum }_{i=1}^N{y}_i}{{\sum }_{i=1}^N(1-y_i)}\right)$。从而可以由$F_0$计算对应的负梯度$r_0$，之后开始对梯度进行拟合。
5. 对$(x,r_{m-1})$用CART回归树进行最优拟合（可对决策树的生成进行具体设置，树不易过深），所得决策树叶节点$j$对应的估计值计算公式为：
   ${\gamma }_{mj}=\frac{{\sum }_{x_i\in R_{mj}{r}_{m-1,i}}}{{\sum }_{x_i\in R_{mj}}(y_i-r_{m-1,i})\cdot (1-y_i+r_{m-1,i})}$（$L^{\prime }=0$时$L$可获极值，而$L^{\prime }$可按泰勒展开式展开一次，从而可解得$f_m(x)=\frac{\sum y_i-p_i}{\sum p_i\ast (1-p_i)}$，将$p$由$r=y-p$表示即可参考），$r_{m-1,i}$是样本$x_i$在上轮中的梯度值， $R_{mj}$是第$m$轮生成的第$j$个叶节点构成的空间$R$。实际是模型乘以模型对应的权重后的结果，可以认为是既有负梯度方向（树实现了对上轮的梯度的最大拟合），又有学习步长的值。
6. 综上，第$m$轮迭代后，总体模型$F_m(x)=F_{m-1}(x)+{\sum }_{j=1}^J{\gamma }_{mj}I(x\in R_{mj})$，$I(x\in R_{mj})$是当$x$在第$m$颗树的第$j$叶节点空间$R$时为1，否则为0。
   属于1分类的概率为$p_i=\frac{1}{1+e^{-F(x_i)}}$；属于0分类的概率为$p_i=\frac{e^{-F(x_i)}}{1+e^{-F(x_i)}}$
7. 重复3~6，直到达到指定迭代次数、梯度变化小于阈值时停止。

B）以指数损失作为损失函数为：$y\in \{-1,+1\}$

1. 损失函数：$L(y,F(x))=log(1+exp(-2yF(x)))$，$F(x)=\frac{1}{2}log[\frac{Pr(y=1|x)}{Pr(y=-1|x)}]$，其中$Pr(y=1|x)$是预测$x$为1的概率，$Pr(y=-1|x)$是预测x为-1的概率。
2. 对应负梯度为：$r_{m-1,i}=-[\frac{\partial L(y,F(x_i)))}{\partial F(x_i)}{]}_{F(x)=F_{m-1}(x)}=\frac{2y_i}{1+exp(2y_i{F}_{m-1}(x_i))}$
3. 初始化$F_0(x)$，之后和计算出$R_{0,i}$
4. 第$m$轮迭代中，用$(x,r_{m-1})$构建决策树，对$r_{m-1}$进行拟合，从而决策树的叶节点$j$的估计值计算公式为：
   ${\gamma }_{mj}=argmi{n}_r{\sum }_{x_i\in R_{mj}}log(1+exp(-2y_i(F_{m-1}(x_i)+\gamma )))$
   一般用近似结果：${\gamma }_{mj}=\frac{{\sum }_{x_i\in R_{mj}}{r}_{m-1,i}}{{\sum }_{x_i\in R_{mj}}|r_{m-1,i}|(2-|r_{m-1,i}|)}$
5. 最终输出模型为$F_m(x)=F_{m-1}(x)+{\gamma }_{mj}I(x_i\in R_{tj})$，从而有$p_{+}(x)=p=\frac{1}{1+e^{-2F(x)}}$，$p_{-}(x)=1-p=\frac{1}{1+e^{2F(x)}}$。从而可以利用概率进行分类。

除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。

GBDT分类算法：多分类

采用OvR，实质上是在每轮训练时都是同时训练多颗树：是否A类一颗树，是否B类一个数，是否C类一棵树…，真实类的概率视为1，其余视为0，从而可以计算负梯度（残差），损失函数用对数似然损失函数。非常好的实例参考
对某轮训练，假设类别数为K，则对数似然损失函数为：$L(y,f(x))=-\sum _{k=1}^K{y}_{k}log{p}_k(x)$，其中如果样本x输出类别为$k$，则$y_k=1$，否则为0。实际是本轮的K颗树之和。
在本轮的K颗树中，每颗树对样本x预测结果为$f_l(x)$，则可综合得属于第$k$类的概率$p_k(x)$的表达式为：$p_k(x)=\frac{exp(f_k(x))}{\sum _{l=1}^{K}exp(f_l(x))}$
结合上面两式，我们可以计算出第$t$轮的第$i$个样本属于类别$l$时的负梯度（伪残差）为：$r_{til}=-[\frac{\partial L(y_i,f(x_i)))}{\partial f(x_i)}{]}_{f_k(x)=f_{l,t-1}(x)}=y_{il}-p_{l,t-1}(x_i)$
这里的误差就是样本$i$在OvR策略下，对应类别为$l$时的真实概率（是则为1，否为0）和$t-1$轮预测概率的差值。
对于生成的决策树，我们各个叶子节点$J$的最佳负梯度拟合值为：$c_{tjl}=\underset{c_{jl}}{argmin}\sum _{i=0}^m\sum _{k=1}^{K}L(y_k,f_{t-1,l}(x)+\sum _{j=0}^J{c}_{jl}I(x_i\in R_{tj}))$
一般使用近似值代替：$c_{tjl}=\frac{K-1}{K}\frac{\sum _{x_i\in R_{tjl}}{r}_{til}}{\sum _{x_i\in R_{til}}|r_{til}|(1-|r_{til}|)}$
从而可以继续对残差进行建模拟合，重复上述过程。
除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。
参考

随机梯度提升SGD

全称Stochastic gradient boosting，每次迭代都对残差样本采用无放回的降采样，用部分样本训练基函数的参数，从而防止过拟合。令训练样本数占所有残差有样本的比例为g，当g=1时为原始模型。推荐使用样本比例$0.5\le g\le 0.8$。
较小的g能够增强随机性，防止过拟合，并且收敛速度快。降采样的另一好处是可以用剩余样本做模型验证。

XGBoost

是eXtreme Gradient Boosting的简写。只能用于回归，对分类是通过预测概率后进行判断所属类别。XGBoost只能接受数值型变量，对于分类变量，需要进行如One-Hot编码的转换。 原文slide 参考
【优点】
当新增分裂带来负增益时，GBM会停止分裂，而XGBoost会一直分裂到指定的最大深度，然后回过头来进行监枝。XGBoost允许在每一轮boosting迭代中使用交叉验证，以便获取最优boosting迭代次数；GMB使用网格搜索，只能检测有限个值。XGBoost和GBM都支持在线学习，即继续已有模型进行训练。最终结果是对各树叶子节点进行加权求和。

1. 除了回归决策树，还可以使用线性分类器。
2. 可以自定义损失函数，用损失函数计算一阶和二阶导；也可以用自定义损失函数的一阶导和二阶导。
3. 通过正则化对树的节点数、节点权重进行惩罚，减少过拟合，降低了方差

在目标函数中添加了正则化。叶子节点个数+叶子节点权重的L2正则化。max_depth,min_child_weight,gamma
列抽样。训练时只使用一部分的特征。colsample_bytree
子采样。每轮计算可以不使用全部样本，类似bagging。包括subsample。
early stopping。如果经过固定的迭代次数后，并没有在验证集上改善性能，停止训练过程。
shrinkage。调小学习率增加树的数量，为了给后面的训练留出更多的空间。减小learning_rate，同时增加estimator

4. xgboost借鉴了随机森林的做法，支持列抽样（拆分节点时？？），不仅能降低过拟合，还能减少计算。GBDT中无此项。
5. 支持缺失值，对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。
6. XGBoost在根据特征进行节点拆分时使用了并行计算（树的建立仍是串行，Boosting一般为串行计算），并使用C语言，速度快。（xgboost在训练之前，先对数据进行排序，然后保存block结构，后面的迭代中重复的使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行）。xgboost还提出了一种可并行的近似直方图算法，对连续变量用于高效地生成候选的分割点（将数据分箱，用分箱的中心线来做对比，从而减少计算最下分割点时的次数）：由于XGBoost是一种boosting算法，树的训练是串行的，不能并行。这里的并行指的是特征维度的并行。在训练之前，每个特征按特征值对样本进行预排序，并存储为Block结构，在后面查找特征分割点时可以重复使用，而且特征已经被存储为一个个block结构，那么在寻找每个特征的最佳分割点时，可以利用多线程对每个block并行计算。
7. 由于“随机森林族”本身具有过拟合特性，因此XGBoost也有该特性。
   
   【理论】
   对模型预测，通过对基函数进行迭代集成作为整体预测结果，每次都是对上次建模后的残差建立新模型，然后和之前的模型结合作为整体最终模型（从而形成迭代）。对损失函数，将基函数视为一个变量，从而可对损失函数使用梯度提升，利用泰勒二阶展开式进行目标损失函数简化，又因迭代时前t-1次结果已定，所以仅与求解当前最优基函数有关。损失函数$L$对基函数$f$进行二阶泰勒展开式来计算，称为XGBoost方法可理解为一阶泰勒展开式就是GBDT）。XGBoost要求弱学习器必须是可以进行回归计算，从而可将历次迭代（树模型就是每棵树）结果求和获取整体最终结果，同GBDT要求相同。
   1、集成算法表示：${\hat{y}}_i^{(t)}={\hat{y}}_i^{(t-1)}+f_t(x_i)={\sum }_{t=1}^T{f}_t(x_i)={\sum }_{t=1}^{T-1}{f}_t(x_i)+f_T(x_i)$，即对第$i$个样本的预测，是通过前$t-1$个基函数预测结果与当前基函数$f_T$预测结果之和，此即为整体结果。
   2、损失函数可表示为$L(f_t)={\sum }_t^{T}L(y_i,{\hat{y}}_i^t)={\sum }_t^{T}L(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+{\sum }_t^T\Omega (f_t)+C$，$f_t$是基函数（如树模型），$\Omega (f_t)$是关于$f_t$的函数的复杂度（如正则项），C是可能的常数项，t是第t次迭代。损失函数可以理解成是根据$泛化误差=偏{差}^2+方差+随机误{差}^2$构造的。

常用损失函数：

• 均方误差：$L(y_i,{\hat{y}}_i)=(y_i-{\hat{y}}_i{)}^2$
• 逻辑回归损失函数：$L(y_i,{\hat{y}}_i)=y_{i}ln(1+e^{-{\hat{y}}_i})+(1-y_i)ln(1+e^{{\hat{y}}_i})$ ，
  一阶导$g=\frac{\partial L(y,F_{t-1})}{F_{t-1}}=-y(1-\frac{1}{1+e^{F_{t-1}}})+(1-y)\frac{1}{1+e^{-y_{t-1}}}=Pred-Label$
  二阶导$h=\frac{{\partial }^{2}L(y,F_{t-1})}{F_{t-1}}=\frac{e^{-y_{t-1}}}{(1+e^{-y_{t-1}}{)}^2}=Pred\ast (1-Pred)$

3、通过泰勒展开式对损失函数进行简化：
由于二阶泰勒展开式$f(x+△x)\approx f(x)+f^{\prime }(x)△x+\frac{1}{2}{f}^{\prime \prime }(x)△x^2$，对$L(y_i^t,{\hat{y}}_i^{(t-1)})$，因$y_i^t$是已知值，所以对第t次迭代$L(y_i^t,{\hat{y}}_i^{(t-1)})可表示为F({\hat{y}}_i^{(t-1)}+f_t(x_i))$，从而可对$F$按照泰勒展开式进行展开，即：
$F({\hat{y}}_i^{(t-1)}+f_t(x_i))\approx F({\hat{y}}_i^{(t-1)})+f_t(x_i)\ast \frac{\partial F({\hat{y}}_i^{(t-1)})}{\partial {\hat{y}}_i^{(t-1)}}+\frac{1}{2}{f}_t^2(x_i)\ast \frac{{\partial }^{2}F({\hat{y}}_i^{(t-1)})}{\partial ({\hat{y}}_i^{(t-1)}{)}^2}\approx l(y_i^t,{\hat{y}}_i^{(t-1)})+f_t(x_i)\ast \frac{\partial l(y_i^t,{\hat{y}}_i^{(t-1)})}{\partial {\hat{y}}_i^{(t-1)}}+\frac{1}{2}{f}_t^2(x_i)\ast \frac{{\partial }^{2}l(y_i^t,{\hat{y}}_i^{(t-1)})}{\partial ({\hat{y}}_i^{(t-1)}{)}^2}\approx l(y_i^t,{\hat{y}}_i^{(t-1)})+f_t(x_i)\ast g_i+\frac{1}{2}{f}_t^2(x_i)\ast h_i={\sum }_i^m[l(y_i,{\hat{y}}_i^{(t-1)})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]$，其中m是所有样本，$l(y_i^t,{\hat{y}}_i^{(t-1)})$是根据之前预测结果得到的常量。
对${\sum }_t^T\Omega (f_t)={\sum }_t^{T-1}\Omega (f_t)+\Omega (f_T)$，其中${\sum }_t^{T-1}\Omega (f_t)$是根据前$T-1$次迭代获得的常量。
综合上边，将常量剔除，总体损失函数通过泰勒二阶展开式可简化为$L(f_t)={\sum }_t^{T}L(y_i,{\hat{y}}_i^t)={\sum }_t^{T}L(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+{\sum }_t^T\Omega (f_t)={\sum }_i^m[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)$，此时只需对第t次迭代找到最优的基模型$f_t$即可（不是GBDT中用来求极值，只是进行简化）。

上式含义：在尽可能对目标值进行拟合以实现预测误差尽可能小的基础上，弱学习器应当有尽可能少的节点，节点取值也尽量偏差不大（防止过拟合风险）

4、对基函数是树模型的损失函数，用树的叶节点表示基函数
对基函数是决策树模型的$f(x)$，其结果可表示为叶节点数T、叶节点的值$w=(w_1,w_2,\dots w_T)$的组合，样本$x$在决策树中的结果可表示为$f(x)=w_{q(x)}$，其中$q(x)$是第$q$个节点。可以对叶节点数$T$和叶节点值$w$(拟合得到的)分别施加惩罚项，得到：$\Omega (f_t)=\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_j^2$，其中$T$是决策树叶节点个数，$w_j$是第$j$个叶节点对应的值（后面会被求解出来）。公式对决策树的惩罚方式不是唯一的，可定义其他形式，如L1正则项$\frac{1}{2}\alpha {\sum }_{j=1}^T|w_j|$，或是L1+L2正则项一起用。引入正则项控制过拟合是GBDT没有的。
对第 t t