Separable Convolution 原理讲解及计算量和参数量比较分析

卷积神经网络中的Separable Convolution

0、前言

移动端设备的硬件性能限制了神经网络的规模。本文介绍一种被称为Separable Convolution的卷积运算方式。它将传统卷积分解为Depthwise Convolution与Pointwise Convolution两部分，有效的减小了参数数量。

卷积神经网络在图像处理中的地位已然毋庸置疑。卷积运算具备强大的特征提取能力、相比全连接又消耗更少的参数，应用在图像这样的二维结构数据中有着先天优势。然而受限于目前移动端设备硬件条件，显著降低神经网络的运算量依旧是网络结构优化的目标之一。本文所述的Separable Convolution就是降低卷积运算参数量的一种典型方法。

1、常规卷积运算

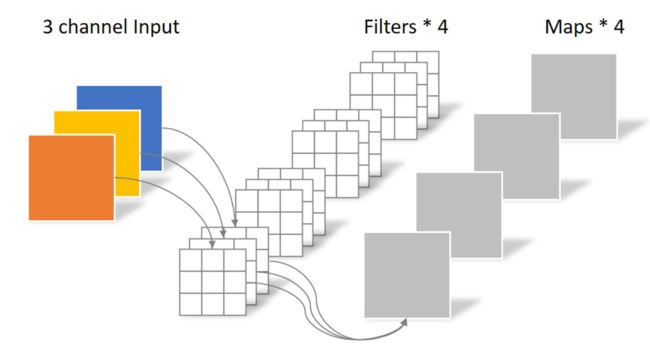
假设输入层为一个大小为64×64像素、三通道彩色图片，输入维度即为64×64×3。经过一个包含4个Filter的卷积层，每个卷积核都是匹配的具有三个通道（即为对应上输入的三个通道），设置卷积核大小为3×3，最终输出通道为4，输出4个Feature Map，且尺寸与输入层相同（在有padding的情况下）。整个过程可以用下图来概括。

此时，卷积层共4个Filter，每个Filter包含了3个通道，每个通道的大小为3×3。因此卷积层的参数数量可以用如下公式来计算：

$$N_{std}=4\times 3\times 3\times 3=108$$

2、Separable Convolution

Separable Convolution在Google的Xception[1]以及MobileNet[2]论文中均有描述。它的核心思想是将一个完整的卷积运算分解为两步进行，分别为Depthwise Convolution与Pointwise Convolution。

2.1 Depthwise Convolution

同样是上述例子，一个大小为64×64像素、三通道彩色图片首先经过第一次卷积运算，不同之处在于：

上面提到的普通卷积的操作是每一个卷积核因为有多个通道所以是同时接收整个输入的全部进行卷积输出一个Feature Map。

但是此次的卷积完全是在二维平面内进行，且Filter的数量与输入的通道数量相同。所以一个三通道的图像经过运算后生成了3个Feature map，如下图所示。

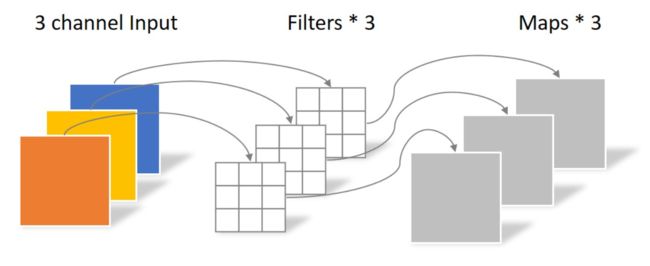
其中一个Filter只包含一个大小为3×3的Kernel，卷积部分的参数个数计算如下：

$$N_{depthwise}=3\times 3\times 3=27$$
Depthwise Convolution完成输出后的Feature map的通道数量与输入层的通道数量相同，但是这种运算对输入层的每个channel独立进行卷积运算后就结束了，没有有效的利用不同Feature map在相同空间位置上的信息。因此需要增加另外一步操作来将这些Feature map进行组合生成新的Feature map，即接下来的Pointwise Convolution。

2.2 Pointwise Convolution

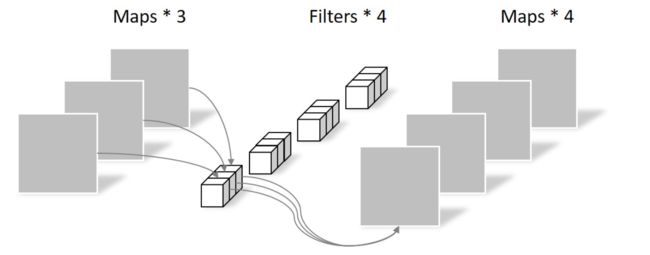
Pointwise Convolution的运算与常规卷积运算非常相似，不同之处在于卷积核的尺寸为 1×1×M，M为上一层的channel。所以这里的卷积运算会将上一步的Feature map在深度方向上进行加权组合，生成新的Feature map。有几个Filter就有几个Feature map。如下图所示。

由于采用的是1×1卷积的方式，此步中卷积涉及到的参数个数可以计算为：

$$N_{pointwise}=1\times 1\times 3\times 4=12$$

经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

3、对比

3.1参数数量对比

常规卷积的参数个数为：
$$N_{std}=4\times 3\times 3\times 3=108$$
Separable Convolution的参数由两部分相加得到：
$$\begin{array}{rl}{N}_{depthwise}& =3\times 3\times 3=27\\ N_{pointwise}& =1\times 1\times 3\times 4=12\\ N_{separable}& =N_{depthwise}+N_{pointwise}=39\end{array}$$

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约$\frac{1}{3}$。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。

3.2 浮点数乘法次数对比

参数设置如下（假设有padding保证输入输出Feature Map大小相同，且没有空洞卷积，且补偿为1）
$$\begin{array}{rl}{C}_{in}& :卷积核通道数量，也就是输入的FeatureMap的通道数量\\ C_{out}& :卷积核通道数量，也就是最终输出的FeatureMap的通道数量\\ W,H& :输入输出FeatureMap的长宽大小\\ w,h& :卷积核的长款大小\end{array}$$

常规卷积计算量：

$$\begin{array}{rl}输出FeatureMap一个通道中的一个点所需要的计算量& :w\times h\times C_{in}\\ 输出FeatureMap一个通道所需要的计算量& :w\times h\times C_{in}\times W\times H\\ 输出FeatureMap所需要的计算量& :w\times h\times C_{in}\times W\times H\times C_{out}\end{array}$$

上面例子中实际计算量为：
$$3\times 3\times 3\times 64\times 64\times 3\times 4=1327104$$

可分离卷积计算量对比：

Depthwise Convolution计算量
$$\begin{array}{rl}输出FeatureMap一个通道中的一个点所需要的计算量& :w\times h\\ 输出FeatureMap一个通道所需要的计算量& :w\times h\times W\times H\\ 输出FeatureMap所需要的计算量& :w\times h\times W\times H\times C_{in}\end{array}$$
Pointwise Convolution计算量
$$\begin{array}{rl}输出FeatureMap一个通道中的一个点所需要的计算量& :1\times 1\times C_{in}\\ 输出FeatureMap一个通道所需要的计算量& :1\times 1\times C_{in}\times W\times H\\ 输出FeatureMap所需要的计算量& :1\times 1\times C_{in}\times W\times H\times C_{out}\end{array}$$
最终计算量为：
$$\begin{gathered} DepthwiseConvolution+PointwiseConvolution \\ w\times h\times W\times H\times C_{in}+1\times 1\times C_{in}\times W\times H\times C_{out} \end{gathered}$$

上面例子中实际的计算量为：
$$3\times 3\times 64\times 64\times 3+1\times 1\times 3\times 64\times 64\times 4=159744$$

相差倍数：

$$\begin{array}{rl}& \frac{w\times h\times C_{in}\times W\times H\times C_{out}}{w\times h\times W\times H\times C_{in}+1\times 1\times C_{in}\times W\times H\times C_{out}}\\ =& \frac{w\times h\times C_{out}}{w\times h+C_{out}}\\ =& \frac{1}{\frac{1}{w\times h}+\frac{1}{C_{out}}}\end{array}$$

卷积核越大，输出通道越多压缩比例越大

LAST、参考文献

Xception: Deep Learning with Depthwise Separable Convolutions, François Chollet
MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
卷积神经网络中的Separable Convolution