【初级算法】LC——3.多种办法解决旋转数组

本期难点：翻转数组

对指定区间进行三次翻转就能得到最终的结果。

题目说明：

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

进阶：

• 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
• 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

提示：

1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

题目要求

将数组比作齿轮，而我们的任务就是将这个齿轮向右移动k 格。但是最少需要提出三种解决方法，其中要有包含空间限制为O(1) 的方法。

方法一：使用额外数组

通过计算将每个元素放到额外数组中正确的位置上，再将额外数组中的元素拷贝回原数组中。

• (i+k)%numsSize 是为了得出那些超出数组长度，要回到数组前面的位置。

void rotate(int* nums, int numsSize, int k){
     
    int a[numsSize];	// 声明一个名为a 的额外数组

    for(int i = 0; i < numsSize; i++){
     
        a[(i+k)%numsSize] = nums[i];	// 将原数组中的元素按照正确的顺序存放到a 数组中
    }

    for(int i = 0; i < numsSize; i++){
     
        nums[i] = a[i];	// 将a 数组中的元素替换掉原数组中的元素
    }
}

方法二：移动数组

每次循环都将数组中的元素向后移动一位，k 位就移动k 次。

• 这里我们注意，因为要将数组往后移动，所以我们要提前保存尾元素
• 并且将尾元素放到首元素上
• 而后就是不断的移动元素

void rotate(int* nums, int numsSize, int k){
     
    int temp, previous;		// 声明两个int 类型用来临时保存数组
    for(int i = 0; i < k; i++){
     	// 将数组向后移动k 次
        previous = nums[numsSize - 1];	// previous 保存数组中的尾元素
        for(int j = 0; j < numsSize; j++){
     	// 将整个数组向后移动1 位
            temp = nums[j];
            nums[j] = previous;
            previous = temp;
        }
    }
}

方法三：翻转数组
当我们对数组的元素向右移动k 次时

• k 为移动次数，n 为数组长度，mod 为 %；
• 尾部k mod n 个元素会移动到数组头部，其余元素向后移动k mod n 个位置
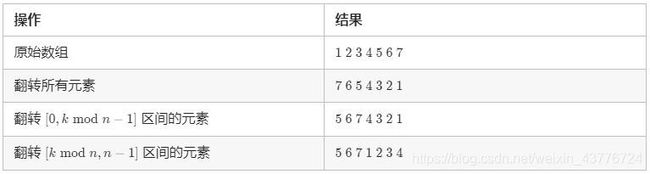
• 那我们可以通过三次翻转来实现这个目标

1. 我们可以先将所有元素翻转，这样尾部的k mod n 个元素就被移动到数组头部；
2. 然后我们再翻转[0, k mod n - 1] 区间的元素；
3. 最后翻转[k mod n, n - 1] 区间的元素，就能得到最后的结果。
   

void rotate(int* nums, int numsSize, int k){
     
    k %= numsSize;	// 当k > numsSize 时，k %= numsSize 就能得出最终元素的移动值。
    reverse(nums, 0, numsSize-1);
    reverse(nums, 0, k-1);
    reverse(nums, k, numsSize-1);
}

void reverse(int* nums, int start, int end){
     
    while(start < end){
     	// 对给定区间进行前后互换
        int temp = nums[end];
        nums[end] = nums[start];
        nums[start] = temp;
        start++;
        end--;
    }
}

以上的三种方法使用额外空间的前两种方法最容易理解，但是带来的时间复杂度也更高。而最后一种翻转数组，虽然难理解了一点，但是只要理解了，就会对于这种题目如鱼得水。

以上就是本篇文章的全部内容了，如果觉得有帮助到你的，

麻烦点赞转发收藏！！！

我们下期再见！

---

在更新技术文章的同时，我还会更新我的学习方法到知乎上，如果大家感兴趣的可以去看一下。