编程作业（python）| 吴恩达 机器学习（6）支持向量机 SVM

$$\ast \ast \ast 点击查看:吴恩达机器学习——整套笔记+编程作业详解\ast \ast \ast$$

作业及代码：https://pan.baidu.com/s/1L-Tbo3flzKplAof3fFdD1w 密码:oin0
本次作业的理论部分：吴恩达机器学习（七）支持向量机
编程环境：Jupyter Notebook

1. 线性 SVM

任务

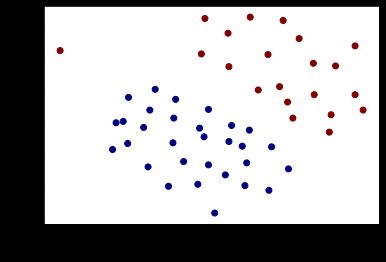
观察惩罚项系数 C 对决策边界的影响，数据集：data/ex6data1.mat

在理论部分，我们得到SVM的代价函数为：
$$J(\theta )=C\sum _{i=1}^m\left[y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)})\right]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$其中C为误差项惩罚系数，C越大，容错率越低，越易过拟合。

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt

data = sio.loadmat('./data/ex6data1.mat')
X,y = data['X'],data['y']

def plot_data():
    plt.scatter(X[:,0],X[:,1],c = y.flatten(), cmap ='jet')
    plt.xlabel('x1')
    plt.ylabel('y1')

plot_data() # 绘制原始数据

由图可知，左上角的那个数据点为异常点（误差点）。

Scikit-learn ，kernel=‘linear’

简称 sklearn，参考官方中文文档：http://sklearn.apachecn.org
提供了很多机器学习的库，本次作业主要也是用它来解决SVM的问题

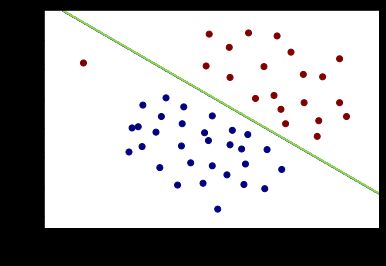
• C = 1

from sklearn.svm import SVC 

svc1 = SVC(C=1,kernel='linear') #实例化分类器，C为误差项惩罚系数，核函数选择线性核
svc1.fit(X,y.flatten())			#导入数据进行训练

>>> svc1.score(X,y.flatten())		#分类器的准确率
> 0.9803921568627451

# 绘制决策边界
def plot_boundary(model):
    x_min,x_max = -0.5,4.5
    y_min,y_max = 1.3,5
    xx,yy = np.meshgrid(np.linspace(x_min,x_max,500),
                       np.linspace(y_min,y_max,500))
    z = model.predict(np.c_[xx.flatten(),yy.flatten()])
    
    zz = z.reshape(xx.shape)
    plt.contour(xx,yy,zz)

plot_boundary(svc1)
plot_data()

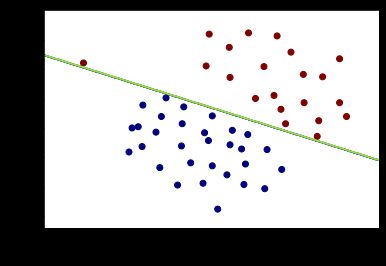
• C = 100

svc100 = SVC(C=100,kernel='linear')
svc100.fit(X,y.flatten())

>>>svc100.score(X,y.flatten())
> 1.0

#绘制决策边界
plot_boundary(svc100)
plot_data()

结论

误差项惩罚系数C越大，容错率越低，越易过拟合。

---

2. 非线性 SVM

任务

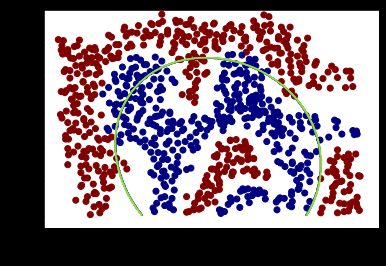
使用高斯核函数解决线性不可分问题，并观察 $\sigma$ 取值对模型复杂度的影响。数据集：data/ex6data2.mat

高斯核函数公式：
$$K\left({\mathbf{x}}_1,{\mathbf{x}}_2\right)=\exp \left\{-\frac{{\Vert {\mathbf{x}}_1-{\mathbf{x}}_2\Vert }^2}{2{\sigma }^2}\right\}$$

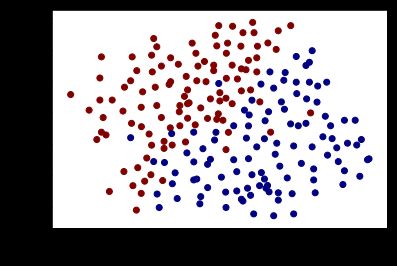
data = sio.loadmat('./data/ex6data2.mat')
X,y = data['X'],data['y']

def plot_data():
    plt.scatter(X[:,0],X[:,1],c = y.flatten(), cmap ='jet')
    plt.xlabel('x1')
    plt.ylabel('y1')

plot_data() # 绘制原始数据

Scikit-learn ，kernel=‘rbf’

• $\sigma =1$ ，注意：sklearn中的$\sigma$表示为gammer，高斯核表示为rbf

svc1 = SVC(C=1,kernel='rbf',gamma=1) #实例化分类器，C为误差项惩罚系数，核函数选择高斯核
svc1.fit(X,y.flatten())					#导入数据进行训练

>>> svc1.score(X,y.flatten())			#分类器的准确率
> 0.8088064889918888

# 绘制决策边界
def plot_boundary(model):
    x_min,x_max = 0,1
    y_min,y_max = 0.4,1
    xx,yy = np.meshgrid(np.linspace(x_min,x_max,500),
                       np.linspace(y_min,y_max,500))
    z = model.predict(np.c_[xx.flatten(),yy.flatten()])
    
    zz = z.reshape(xx.shape)
    plt.contour(xx,yy,zz)

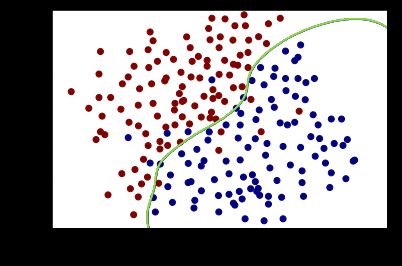
plot_boundary(svc1)
plot_data()

• $\sigma =50$
  
• $\sigma =1000$
  

结论

$\sigma$ 值越大，模型复杂度越高，同时也越易过拟合
$\sigma$ 值越小，模型复杂度越低，同时也越易欠拟合

---

3. 寻找最优参数 C 和 $\sigma$

数据集：data/ex6data3.mat

mat = sio.loadmat('data/ex6data3.mat')
X, y = mat['X'], mat['y']				# 训练集
Xval, yval = mat['Xval'], mat['yval']	# 验证集

def plot_data():
    plt.scatter(X[:,0],X[:,1],c = y.flatten(), cmap ='jet')
    plt.xlabel('x1')
    plt.ylabel('y1')

plot_data() # 绘制原始数据

# C 和 σ 的候选值
Cvalues = [3, 10, 30, 100,0.01, 0.03, 0.1, 0.3,1 ]  #9
gammas =  [1 ,3, 10, 30, 100,0.01, 0.03, 0.1, 0.3]  #9

# 获取最佳准确率和最优参数
best_score = 0
best_params = (0,0)

for c in Cvalues:
    for gamma in gammas:
        svc = SVC(C=c,kernel='rbf',gamma=gamma)
        svc.fit(X,y.flatten())					# 用训练集数据拟合模型
        score = svc.score(Xval,yval.flatten())  # 用验证集数据进行评分
        if score > best_score:
            best_score = score
            best_params = (c,gamma)
>>> print(best_score,best_params)
> 0.965 (3, 30) 

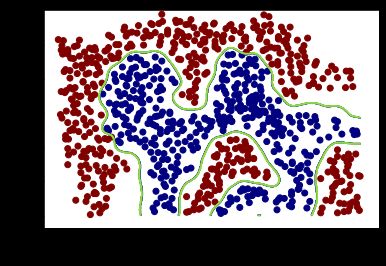
注意：获取到的最优参数组合不只有一组，更改候选值的顺序，最佳参数组合及其对应的决策边界也会改变

svc2 = SVC(C=3,kernel='rbf',gamma=30)

def plot_boundary(model):
    x_min,x_max = -0.6,0.4
    y_min,y_max = -0.7,0.6
    xx,yy = np.meshgrid(np.linspace(x_min,x_max,500),
                       np.linspace(y_min,y_max,500))
    z = model.predict(np.c_[xx.flatten(),yy.flatten()])
    
    zz = z.reshape(xx.shape)
    plt.contour(xx,yy,zz)

plot_boundary(svc2)
plot_data()

4. 垃圾邮件过滤问题

注意：data/spamTrain.mat是对邮件进行预处理后（自然语言处理）获得的向量

# training data
data1 = sio.loadmat('data/spamTrain.mat')
X, y = data1['X'], data1['y']
 
# Testing data
data2 = sio.loadmat('data/spamTest.mat')
Xtest, ytest = data2['Xtest'], data2['ytest']

>>> X.shape,y.shape # 样本数为4000
> ((4000, 1899), (4000, 1))

>>> X # 每一行代表一个邮件样本，每个样本有1899个特征，特征为1表示在跟垃圾邮件有关的语义库中找到相关单词
> array([[0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       ...,
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 1, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0]], dtype=uint8)
       
>>> y # 每一行代表一个邮件样本，等于1表示为垃圾邮件
> array([[1],
       [1],
       [0],
       ...,
       [1],
       [0],
       [0]], dtype=uint8)

# 候选的 C值
Cvalues = [3, 10, 30, 100,0.01, 0.03, 0.1, 0.3,1 ] 

# 获取最佳准确率和最优参数
best_score = 0
best_param = 0

for c in Cvalues:
    svc = SVC(C=c,kernel='linear')
    svc.fit(X,y.flatten())					# 用训练集数据拟合模型
    score= svc.score(Xtest,ytest.flatten()) # 用验证集数据进行评分
    if score > best_score:
        best_score = score
        best_param = c
>>> print(best_score,best_param)
> 0.99 0.03

# 带入最佳参数
svc = SVC(0.03,kernel='linear')
svc.fit(X,y.flatten())
score_train= svc.score(X,y.flatten())
score_test= svc.score(Xtest,ytest.flatten())

>>> print(score_train,score_test)
> 0.99425 0.99

---

附：邮件预处理

with open('data/emailSample1.txt', 'r') as f:
    sampe_email = f.read()
    print(sampe_email)

'''
预处理主要包括以下8个部分：
  1. 将大小写统一成小写字母；
  2. 移除所有HTML标签，只保留内容。
  3. 将所有的网址替换为字符串 “httpaddr”.
  4. 将所有的邮箱地址替换为 “emailaddr”
  5. 将所有dollar符号($)替换为“dollar”.
  6. 将所有数字替换为“number”
  7. 将所有单词还原为词源，词干提取
  8. 移除所有非文字类型
  9.去除空字符串‘’
'''

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from sklearn import svm
import nltk.stem as ns
import re

def preprocessing(email):
    
    # 1. 统一成小写
    email = email.lower()
    
    #2. 去除html标签
    email = re.sub('<[^<>]>', ' ', email)
    
    #3. 将网址替换为字符串 “httpaddr”.
    email = re.sub('(http|https)://[^\s]*', 'httpaddr', email ) 
    
    #4. 将邮箱地址替换为 “emailaddr”
    email = re.sub('[^\s]+@[^\s]+', 'emailaddr', email)
    
     # 5.所有dollar符号($)替换为“dollar”.
    email = re.sub('[\$]+', 'dollar', email) 
    
    # 6.匹配数字，将数字替换为“number”
    email = re.sub('[0-9]+', 'number', email) # 匹配一个数字， 相当于 [0-9]，+ 匹配1到多次
    
    # 7. 词干提取
    tokens = re.split('[ \@\$\/\#\.\-\:\&\*\+\=\[\]\?\!\(\)\{\}\,\'\"\>\_\<\;\%]', email)
    tokenlist=[]

    s = ns.SnowballStemmer('english')
        
    for token in tokens:
        
        # 8. 移除非文字类型
        email  = re.sub('[^a-zA-Z0-9]', '', email)
        stemmed = s.stem(token)
    
        # 9.去除空字符串‘’
        if not len(token): continue
        tokenlist.append(stemmed)  
        
    return tokenlist


email = preprocessing(sampe_email)
 
def email2VocabIndices(email, vocab):
    """提取存在单词的索引"""
    token = preprocessing(email)
    print(token)
    index = [i for i in range(len(token)) if token[i] in vocab]
    return index 

def email2FeatureVector(email):
    """
    将email转化为词向量，n是vocab的长度。存在单词的相应位置的值置为1，其余为0
    """
    df = pd.read_table('data/vocab.txt',names=['words'])
    vocab = df.values  # return array
    vector = np.zeros(len(vocab))  # init vector
    vocab_indices = email2VocabIndices(email, vocab) 
    print(vocab_indices)# 返回含有单词的索引
    # 将有单词的索引置为1
    for i in vocab_indices:
        vector[i] = 1
    return vector

import pandas as pd
vector = email2FeatureVector(sampe_email)
>>> print('length of vector = {}\nnum of non-zero = {}'.format(len(vector), int(vector.sum())))
> ['anyon', 'know', 'how', 'much', 'it', 'cost', 'to', 'host', 'a', 'web', 'portal', '\n', '\nwell', 'it', 'depend', 'on', 'how', 'mani', 'visitor', 'you', 're', 'expect', '\nthis', 'can', 'be', 'anywher', 'from', 'less', 'than', 'number', 'buck', 'a', 'month', 'to', 'a', 'coupl', 'of', 'dollarnumb', '\nyou', 'should', 'checkout', 'httpaddr', 'or', 'perhap', 'amazon', 'ecnumb', '\nif', 'your', 'run', 'someth', 'big', '\n\nto', 'unsubscrib', 'yourself', 'from', 'this', 'mail', 'list', 'send', 'an', 'email', 'to', '\nemailaddr\n\n']
[0, 1, 2, 3, 4, 5, 6, 7, 9, 13, 14, 15, 16, 17, 19, 20, 21, 23, 24, 25, 26, 27, 28, 29, 32, 33, 35, 36, 37, 39, 41, 42, 43, 47, 48, 49, 50, 52, 53, 54, 56, 57, 58, 59, 60, 61]
length of vector = 1899
num of non-zero = 46

>>> vector.shape
> (1899,)