【数据分析】基于时间序列的预测方法(2021-01-08)
时间序列预测
目录
- 时间序列预测
-
- 1.时间序列介绍
- 2.原始数据集
- 3.导入数据
- 4.检测时间序列的平稳性
- 5.如何使时间序列平稳
-
- 5.1 估计和消除趋势
-
- 5.1.1 对数转换
- 5.1.2 移动平均
- 5.2 消除趋势和季节性
-
- 5.2.1 差异化
- 5.2.2 分解
- 6.预测时间序列
-
- 6.1 AR Model
- 6.2 MA Model
- 6.3 Combined Model
- 6.4 恢复到原始比例
1.时间序列介绍
时间序列(Time Series,TS)是数据科学中比较有意思的一个领域。顾名思义,TS是按固定时间间隔收集的数据点的集合。对这些数据进行分析以确定长期趋势,以便预测未来或执行其他形式的分析。但是TS又与常规回归问题不同。
- 它是时间相关的。因此,在这种情况下,“观测值是独立的线性回归模型”这个基本假设不成立。
- 随着趋势的增加或减少,大多数TS具有某种形式的季节性趋势,即特定时间范围内的变化。例如,一件羊毛夹克的销量,随着时间不断向前推进,我们会发现在冬季总是有更高的销量。
2.原始数据集
我们以一家超市某种物品的销量作为模拟分析的对象。第一列是字符串格式的日期(从20200101到20200523),第二列是销量情况。
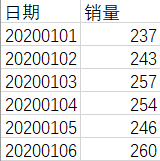
数据集和代码放在了我的GitHub上,需要的朋友可以自行下载:https://github.com/Beracle/01-Time-Series-Forecast.git
3.导入数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
导入数据,输出前几个数据看一下格式。
data = pd.read_csv('Sales.csv')
print(data.head())
data.dtypes
dateparse = lambda dates: pd.datetime.strptime(dates, '%Y%m%d')
data = pd.read_csv('Sales.csv', parse_dates=['日期'], index_col='日期',date_parser=dateparse)
print ('\n Parsed Data:')
print (data.head())
- parse_dates:指定包含时间信息的列。如上所述,列名称为“日期”。
- index_col:对TS数据使用Pandas的一个关键思想是索引必须是描述时间信息的变量。因此,此参数告诉Pandas使用“日期”列作为索引。
- date_parser:指定了一个将输入字符串转换为datetime变量的函数。默认情况下,Pandas读取格式为“ YYYY-MM-DD HH:MM:SS”的数据。如果数据不是这种格式,则必须手动定义格式。因此,可以使用类似于此处定义的dataparse函数的功能。
我们可以看到数据以时间对象为索引。
data.index
ts = data['销量']
ts.head(10)
ts['2020-01-02']
![]()
查看两个日期之间所有的销量数据。
ts['2020-01-02 ':'2020-01-09 ']

查看2020-01-08之前(包含1月8号这一天)所有的销量情况。
ts[:'2020-01-08']
ts['2020-01']
4.检测时间序列的平稳性
如果TS的统计特性(例如均值,方差)随时间保持恒定,则称TS是固定的。大多数TS模型都是在TS固定的前提下工作的。所以在一般情况下,我们可以认为,如果某个TS随时间具有特定的行为,那么将来很有可能会遵循相同的行为。而且,与非平稳序列相比,平稳序列有关的理论更加成熟并且更易于实现。
平稳性有着非常严格的标准定义。但是,出于实际考虑,如果该序列随时间具有不变的统计特性,则可以假定该序列是平稳的。本文提到的平稳性需满足:
- 恒定均值
- 恒定方差
- 不依赖时间的自协方差
原始销量变化趋势图。
plt.plot(ts)

显然,数据总体上呈上升趋势,并且存在一些季节性变化。但是,这种视觉推断并不总是准确的。因此,我们会使用以下方法检查平稳性:
- 绘制移动统计数据:通过绘制移动平均值或移动方差趋势图,判断其是否随时间变化。
- Dickey-Fuller检验:这是用于检查平稳性的统计检验之一。这里的零假设是TS是非平稳的。测试结果包括测试统计量和一些差异置信度的临界值。如果“检验统计量”小于“临界值”,我们可以拒绝原假设并说该序列是平稳的。
下面的test_stationarity()函数则包含了上面提到的两种方法。
!pip install statsmodels
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = timeseries.rolling(window=12).mean()
rolstd = timeseries.rolling(window=12).std()
#Plot rolling statistics:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
#Perform Dickey-Fuller test:
print('Results of Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)
test_stationarity(ts)
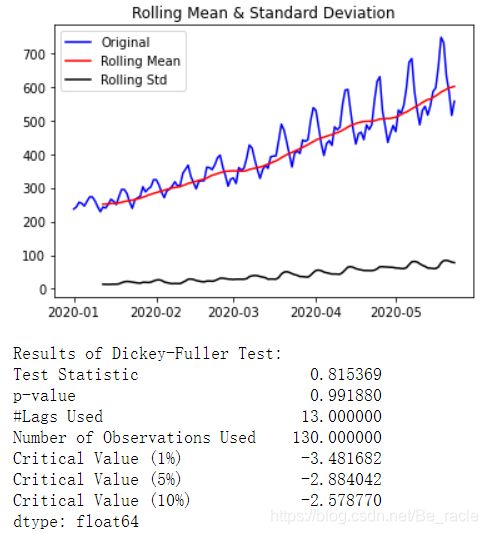
尽管标准差变化很小,但均值显然随时间增加,这并不是平稳序列。测试统计数据也不仅是含有临界值。注意:应该连同符号比较,而不是绝对值。
5.如何使时间序列平稳
尽管在许多TS模型中都采用了平稳性假设,但实际的时间序列几乎没有一个是平稳的。所幸我们已经找到了一些使时间序列平稳的方法。实际上,要使一个时间序列完全固定几乎是不可能的,但是我们尝试使其尽可能接近平稳。
导致TS不平稳的背后原因主要有两个:
- 趋势——均值随时间变化。例如,乘客数量随时间增长。
- 季节性——在特定时间范围内的变化。例如,由于加薪或节日的影响,人们可能会在特定月份购买汽车。
基本原理是对时间序列中的趋势和季节性建模或估计,并将其从序列中删除以得到固定的时间序列。然后在该时间序列上实施统计预测技术。最后一步则是通过应用趋势和季节性约束将预测值转换为原始比例。
下面会讨论多种方法。有的可能效果很好,而有的可能效果不好。但是,我们的目的是掌握所有的方法,而不是仅仅关注眼前的问题。
5.1 估计和消除趋势
5.1.1 对数转换
减小趋势的常用技巧是转换。例如,在上文原始数据趋势图中,我们可以清楚地看到存在明显的上升趋势。因此,我们可以应用变换来惩罚较高的值。可以取对数,平方根,立方根等。为简单起见,在这里进行对数转换(注意下图中纵坐标的变化)。
ts_log = np.log(ts)
plt.plot(ts_log)
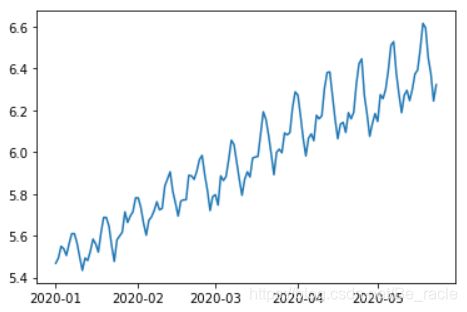
在这种简单的情况下,很容易看到数据中的向前趋势。但是在有噪音的情况下它不是很直观。因此,我们可以先使用一些技术来估算或建模,然后将其从序列中消除。常用的方法有:
- 聚类。在一段时间内取平均值,例如每月/每周平均值。
- 平滑。取滑动平均值
- 多项式拟合。拟合回归模型。
下面会讨论移动平均技术。
5.1.2 移动平均
在这种方法中,我们根据时间序列的频率取“k”个连续值的平均值。在这里,我们将参数设置为12,即最近12天的数据。
moving_avg = ts_log.rolling(12).mean()
plt.plot(ts_log)
plt.plot(moving_avg,color ='red')
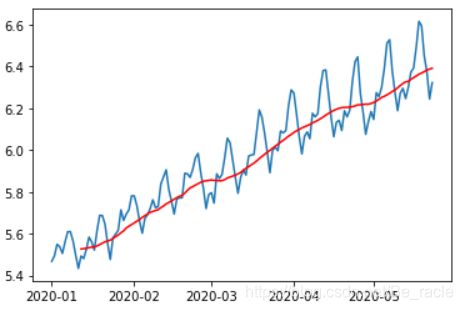
红线表示移动平均值。我们把它从原始时间序列中减去。并且,由于我们取的是最近12个值的平均值,因此前11个值没有定义移动平均值。
ts_log_moving_avg_diff = ts_log - moving_avg
ts_log_moving_avg_diff.head(15)
ts_log_moving_avg_diff.dropna(inplace = True)
test_stationarity(ts_log_moving_avg_diff)
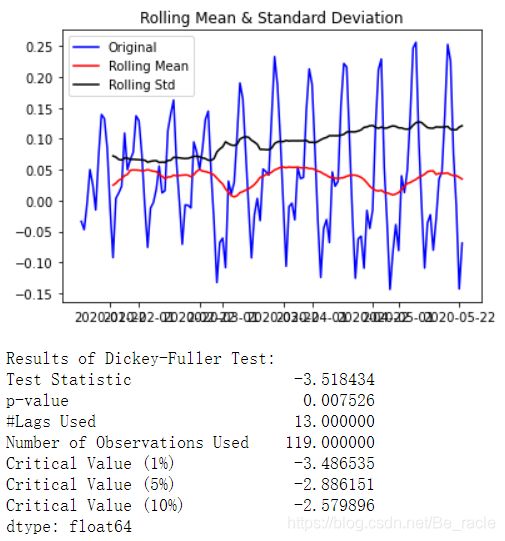
结果看起来还不错。移动平均值发生了变化,但没有特定趋势。另外,测试统计量小于1%的临界值,因此我们可以以99%的置信度说这是一个平稳的序列。
但是,该方法的缺点是必须严格定义时间段。比如,我们可以采用月平均值,但是在复杂的情况下(例如预测股票价格),很难得出一个数字。因此,我们采用“加权移动平均”,其中,最新值的权重更高。分配权重的技术有多种,流行的是指数加权移动平均,其中权重通过衰减因子分配给所有先前的值。
expwighted_avg = pd.DataFrame.ewm(ts_log,halflife = 12).mean()
plt.plot(ts_log)
plt.plot(expwighted_avg,color ='red')
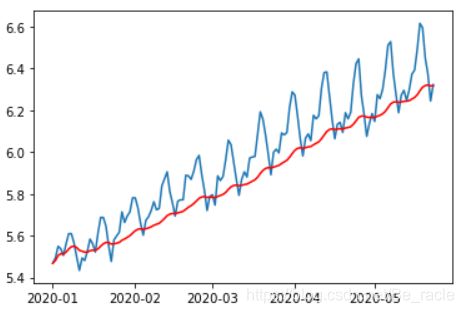
此处的参数“halflife’”用于定义指数衰减量。这只是一个假设,在很大程度上取决于业务领域。其他参数(例如span)也可以用于定义衰减。现在,重复之前的操作,先删除它再检查平稳性.
ts_log_ewma_diff = ts_log - expwighted_avg
test_stationarity(ts_log_ewma_diff)
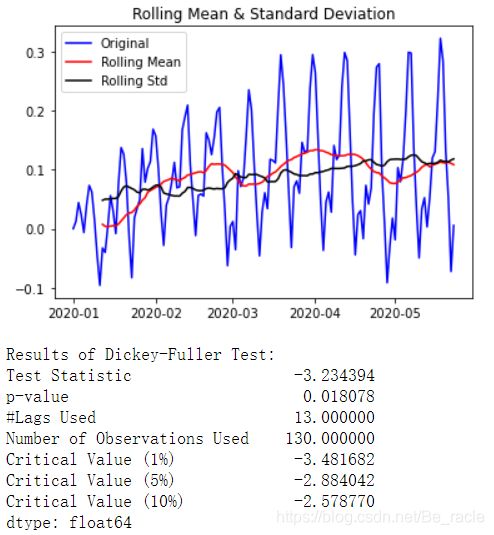
测试统计量小于5%的临界值,因此我们可以以95%的置信度说这是一个平稳的序列。在这种情况下,不会遗漏任何值,因为从一开始所有的值都被赋予了权重。因此,即使没有先前的值也可以使用。
5.2 消除趋势和季节性
前面讨论的简单趋势减少技术并不能在所有情况下都有效,尤其是季节性高的情况下。接下来讨论消除趋势和季节性的两种方法:
- 差异化:以特定的时间差来差异化。
- 分解:对趋势和季节性建模,并将其从模型中删除。
5.2.1 差异化
在这项技术中,我们将特定时刻的观测值与前一时刻的观测值进行了差异。这在改善平稳性方面效果很好。此处使用一次偏移进行差异化。
ts_log_diff = ts_log - ts_log.shift()
plt.plot(ts_log_diff)
ts_log_diff.dropna(inplace = True)
test_stationarity(ts_log_diff)
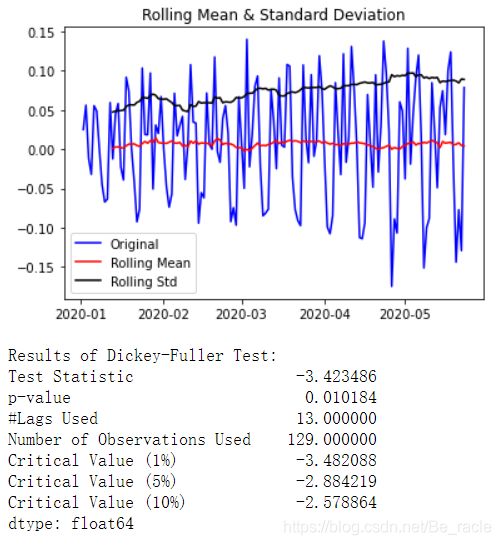
我们可以看到,均值和标准差随时间变化很小。而且,Dickey-Fuller测试统计量小于5%临界值,因此TS处于95%置信度。我们还可以采用二次或三次偏移,这在某些场景下可能会获得更好的结果。
5.2.2 分解
这种方法对趋势和季节性分别建模,然后返回序列的残余部分。
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
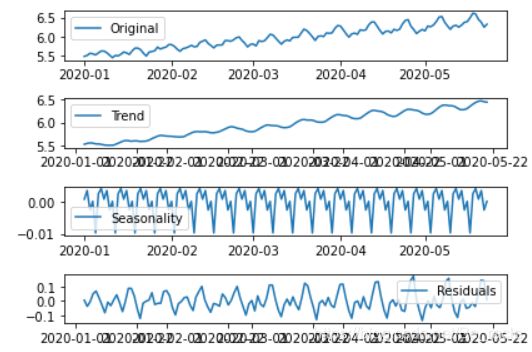
在这里,我们可以看到趋势,季节性和数据已分离,并且可以对残差进行建模。我们再次检查残差的平稳性:
ts_log_decompose = residual
ts_log_decompose.dropna(inplace=True)
test_stationarity(ts_log_decompose)
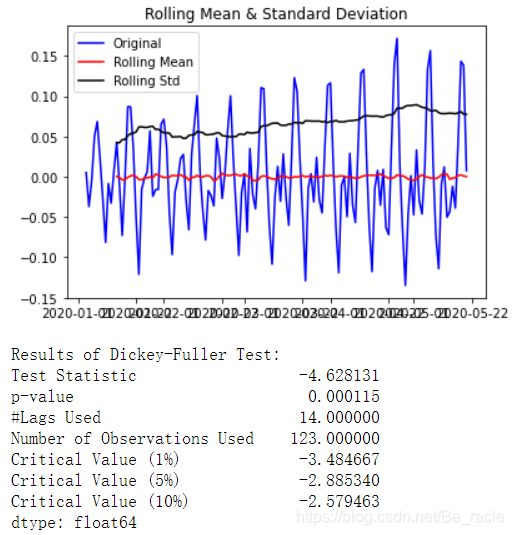
Dickey-Fuller检验统计量明显低于1%临界值。因此,此TS非常接近固定位置。也可以尝试使用高级分解技术,以产生更好的结果。应该注意的是,在这种情况下,将残差转换为原始数据以用于将来的数据不是很直观。
6.预测时间序列
上面谈到的这些不同的技术都可以使TS趋于平稳。现在让我们在差分后的TS上建立模型。这是一种非常流行的技术,并且在这种情况下,将噪声和季节性重新添加到预测残差中相对较容易。执行了趋势和季节性估计技术后,可能出现两种情况:
- 在数值之间没有相关性的一个严格的平稳序列。这是简单的情况,其中我们可以将残差建模为白噪声,但这是非常罕见的。
- 数值之间有重大依赖性的时间序列。在这种情况下,我们需要使用ARIMA之类的统计模型来预测数据。
ARIMA,即自回归移动平均模型,对平稳时间序列的预测只是一个线性(如线性回归)方程。预测变量取决于ARIMA模型的参数(p,d,q):
- AR(Auto-Regressive,自回归)项的数量(p):AR项是因变量的滞后值。例如,如果p为5,则x(t)的预测变量为x(t-1)…x(t-5)。
- MA(Moving Average,移动平均)项的数量(q): MA项是预测方程式中的滞后预测误差。例如,如果q为5,则x(t)的预测变量将为e(t-1)….e(t-5),其中e(i)是第i个瞬时移动平均值与实际值之间的差。
- 差异数(d):这些是非季节性差异数,即在这种情况下,我们采用一阶差分。因此,我们可以传递该变量并置d = 0,或者传递原始变量并置d = 1。两者都会产生相同的结果。
如何确定“ p”和“ q”的值呢?
- 自相关函数(Autocorrelation Function,ACF):它是TS与自身滞后版本之间的相关性的度量。例如,在滞后值为5,ACF会将时间点“t(1)”…“t(2)”处的序列与时间点“t(1)-5”……“ t(2)-5”处的序列进行比较。
- 局部自相关函数(Partial Autocorrelation Function,PACF):此方法在消除了TS与自身滞后版本之间的比较差异后,测量二者的相关性。例如,它将检查滞后值为5的相关性,但删除滞后值为1到4的影响。
差分后,绘制TS的ACF和PACF图。
#ACF and PACF plots:
from statsmodels.tsa.stattools import acf, pacf
lag_acf = acf(ts_log_diff, nlags=20)
lag_pacf = pacf(ts_log_diff, nlags=20, method='ols')
#Plot ACF:
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Autocorrelation Function')
#Plot PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Partial Autocorrelation Function')
plt.tight_layout()

在上图中,0两侧的两条虚线是置信区间,可用于确定“p”和“q”值,如下所示:
- p – PACF的滞后值图表首次超过上限置信区间。如果密切注意,在这种情况下,p = 2。
- q – ACF图表首次超过上限置信区间的滞后值。如果您密切注意,在这种情况下,q = 2。
下面3个不同的ARIMA模型,将分别考虑单独情况和综合情况,并输出RSS。这里的RSS是指残差值,而不是实际的序列。
from statsmodels.tsa.arima_model import ARIMA
6.1 AR Model
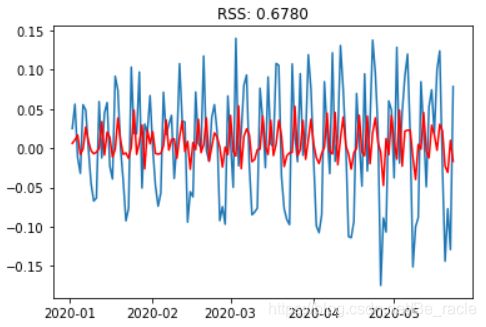
model = ARIMA(ts_log, order=(2, 1, 0))
results_AR = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_AR.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_AR.fittedvalues-ts_log_diff)**2))
6.2 MA Model
model = ARIMA(ts_log, order=(0, 1, 2))
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_MA.fittedvalues-ts_log_diff)**2))
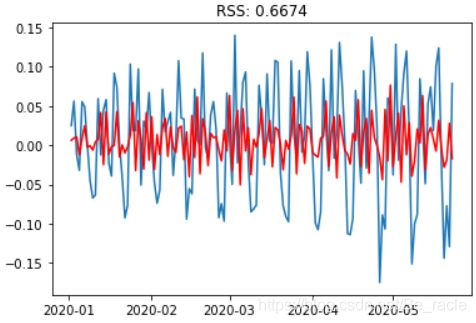
6.3 Combined Model
model = ARIMA(ts_log, order=(2, 1, 2))
results_ARIMA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_ARIMA.fittedvalues-ts_log_diff)**2))

我们可以看到AR和MA模型具有几乎相同的RSS,但结合起来明显更好。现在,最后一个步骤,即将这些值恢复为原始比例。
6.4 恢复到原始比例
由于组合模型提供了最佳结果,因此我们将其缩放回原始值并查看其在该位置的性能如何。第一步是将预测结果存储为单独的序列并进行观察。
predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)
predictions_ARIMA_diff.head()

这些日期从“2020-01-02”开始,而不是“2020-01-01”。因为我们的延迟为1,并且第一个元素之前没有要减去的元素。将差异转换为对数刻度的方法是将这些差异连续添加到基数中。一种简单的方法是先确定索引处的累加和,然后将其加到基数上。累积总和可以找到为:
predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()
predictions_ARIMA_diff_cumsum.head()

接下来,需要将它们添加到基数中。为此,我们创建一个以所有值为基数的序列,并在其中添加差异。在这里,第一个元素是基数本身,并从此开始累加值。
predictions_ARIMA_log = pd.Series(ts_log.iloc[0], index=ts_log.index)
predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum,fill_value=0)
predictions_ARIMA_log.head()

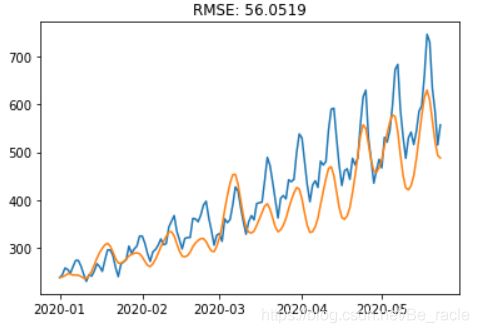
最后一步是利用指数将其还原成原始比例,并与原始序列进行比较。
predictions_ARIMA = np.exp(predictions_ARIMA_log)
plt.plot(ts)
plt.plot(predictions_ARIMA)
plt.title('RMSE: %.4f'% np.sqrt(sum((predictions_ARIMA - ts)**2)/len(ts)))