力扣 leetcode 1319. 连通网络的操作次数 （python）并查集模板快速解及树的高效解

Topic：

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。
网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。
给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

Example_1:

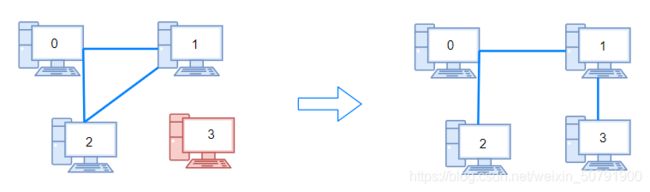
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

Example_2:

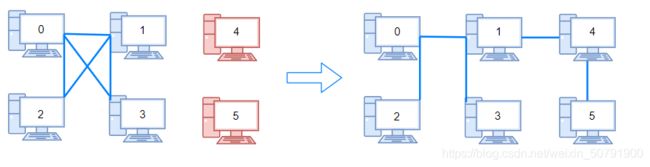
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

Example_3:

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出：-1
解释：线缆数量不足。

Example_4:

输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出：0

Solution_1:

本方法基于并查集模板实现

首先判断不可能连通所有计算机的情况
如果连线数小于计算机数 - 1则不可能连通所有计算机
直接输出 - 1
完成排除所有的不可能连通的情况

我们无需关心如何进行拆线再连接的过程
后面的只要多存在一个连通分量，就有一条多余的边需要操作
则我们需要计算连通分量的个数

计算连通分量:

我们可以通过模板中添加size计算连通分量：
在初始化并查集时同时初始化size为0
每增加一个新节点就增加一个连通分量
同时每合并两个节点就减少一个连通分量

最后直接返回连通分量个数−1即可完成

Code_1：

class UnionFind:
    def __init__(self):
        self.father = {
     }
        self.size = 0

    def find(self,x):
        root = x

        while self.father[root] != None:
            root = self.father[root]

        # 路径压缩
        while x != root:
            original_father = self.father[x]
            self.father[x] = root
            x = original_father
         
        return root
    
    def merge(self, x, y):
        root_x,root_y = self.find(x),self.find(y)
        
        if root_x != root_y:
            self.father[root_x] = root_y
            self.size -= 1

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)

    def add(self, x):
        if x not in self.father:
            self.father[x] = None
        self.size += 1

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        if len(connections)  < n - 1:
            return -1

        uf = UnionFind()

        for j in range(n):
            uf.add(j)

        for i in connections:           
            if uf.is_connected(i[0], i[1]) is False:
                uf.merge(i[0], i[1])

        if uf.size == 1:
            return 0
        else:
            return uf.size - 1

Result_1:

Solution_2:

第一步与思路一相同：
首先判断不可能连通所有计算机的情况
如果连线数小于计算机数 - 1则不可能连通所有计算机
直接输出 - 1
完成排除所有的不可能连通的情况

本思路中并查集是通过list实现的
总体上还是通过记录连通分量来实现算法的
先通过n个节点生成带有节点序号的树father用于记录父节点
之后定义一个find_root函数去通过递归寻找根节点

只要father中记录的父节点与此节点序号（索引）不相等
就去寻找此节点序号记录的上一个节点的父节点
直至找到作为根节点的节点序号（节点序号与father中记录的父节点相同）
如果根节点值不相等（处于不同的连通分量中）
则将其中一个节点的父节点赋值为另一个节点（将两个连通分量相连）

最后就完成了所有的已知连通分量的连接和计算
返回连通分量数减一即可完成

Code_2:

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        if len(connections) + 1 < n: 
            return - 1

        father = list(range(n))

        def find(x):
            if x != father[x]:
                father[x] = find(father[x])
            return father[x]

        for x, y in connections:
            x, y = find(x), find(y)

            if x != y:
                father[y] = x
                n -= 1

        return n - 1

Result_2:

Result_3:

> 如果将递归方法变为递推方法
其效率还会进一步的提高
效果就非常理想了