数据结构之并查集：按秩合并与路径压缩优化

并查集

1.并查集描述

一些有$n$个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。
为了快速解决这些问题，便有了并查集的概念。
并查集维护了一个不相交的动态集的集合$S_1,S_2,\cdots ,S_n$，每个集合将有一个"首领"来标识该集合，我们不关心集合的哪个成员作为"首领"（不排除有些问题需要选择适合特定规则的成员作为首领，例如最大成员做首领）。

2.并查集的三种操作

2.1 makeSet(x) 初始化
以x为唯一成员和"首领"建立一个新集合。

2.2 union(x,y) 合并
将"首领"为x和y的两个集合进行合并，组成一个新集合，新集合的"首领"可以是新集合的任何成员。

2.3 findSet(x) 查询
返回一个指针，指向包含成员x的集合的"首领"。

2.4 例子
以下为例子，下划线部分为"首领"。
初始化：{ A}，{ B}，{ C}，{ D}，{ E}，{ F}，{ G}
合并：{ A，B}，{C，D，E}，{ F，G}
查询：此时对C，D，E进行查找操作将返回同样的结果：D
合并：{A，B，C，D，E}，{ F，G}
查询：此时对A，B，C，D，E进行查找操作将返回同样的结果：D
查询：此时对A，F进行查找操作将返回不同的结果：D，F

3.并查集两种结构

3.1 链式结构

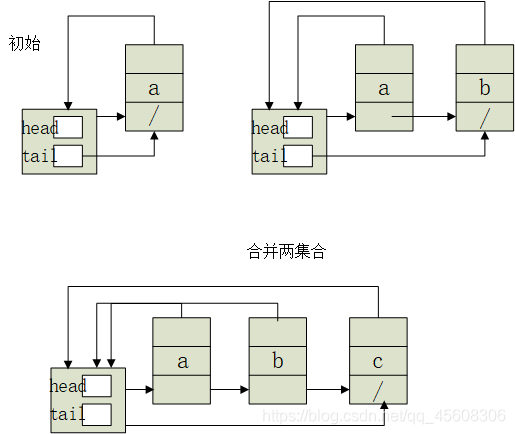
3.2 树结构
树结构并查集由若干颗树组成，树的根结点为该集合的"首领"，树的每个结点只有一个指向父节点的指针和一个数据域。特别注意的是根结点的指针指向自己。
初始化：$n$个只有根结点的树。
合并：树x和树y合并，可使得树y的根结点指向树x的根结点即可完成合并。
查询：对于元素xy，查找其树根结点即可，若树根结点一样，则xy在同一个集合中。

并查集的优化策略

1.按秩合并

1.1 秩的概念
为了更好的描述问题，引入"秩"的概念，某结点的秩是该结点的高度上界。

1.2 考虑如下情况：有$n$个集合需要组合成一个集合。
1）随意合并，有可能使得每次合并都是一个秩较大的树挂载到秩较小的树上，极端情况：

这样，退化为一个近似链表。
2）按秩合并策略，每次都让秩小的树挂载到秩大的树的根上。其最坏情况为，每次都选取相同高度的树进行合并，这样，将使得树变成一个近似的完全二叉树。

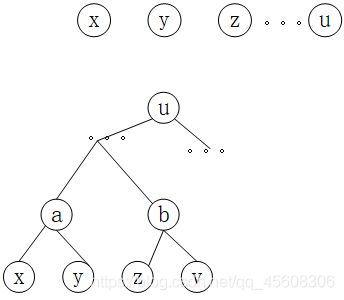
显然，完全二叉树所有结点搜索根结点的平均时间要小于链表的时间。

很容易证明，在树的高度不变的情况下的合并操作的摊还搜索次数要小于加大树高度的情况下的合并操作的摊还搜索次数。
因此，我们希望合并操作时尽可能的不改变树的深度。合并策略为：让秩小的结点所在的树成为秩较大结点所在的树的子树。而当两个树的深度一样时，合并之后树的深度不得不改变，因此仍然需要对秩进行维护。

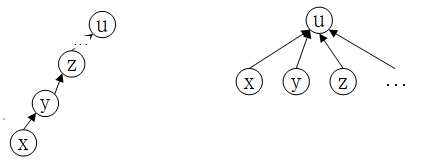
2.路径压缩

为了尽快地找到根结点，减少查询和合并操作的搜索次数，从结点v搜索到根结点时，我们可以将该结点及其所有祖先结点直接指向根结点，这样一来，可以极大地减少那些结点到根结点的搜索次数，这种方法称为路径压缩。

3.性能

《算法导论》对其性能进行详细分析，结论为最坏运行时间为$O(m)\alpha (n)$，其中m为所有操作（包括makeSet,findSet,union）的次数，而n为初始结点数。
$\alpha (n)<4$，故可认为与m成线性关系。

并查集实现

1.维护的成员及构造函数

public class DisjointSet {
     
    private int[] parent;        //标识结点的根结点位置
    private int[] rank;         //记录结点的秩

    public DisjointSet(int num){
         //传入结点数
        parent = new int[num];
        rank = new int[num];
        for (int i = 0; i < num; i++) {
     
            makeSet(i);     //每个结点新建立一个集合
        }
    }
}

2.makeSet(x) 初始化

public void makeSet(int x){
     
    parent[x] = x;
    rank[x] = 0;
}

3.findSet(x) 查询+路径压缩

递归实现：

public int findSet(int x){
     
    if(x!=parent[x])
        parent[x] = findSet(parent[x]);
    return parent[x];
}

非递归实现：

public int findSet(int x){
     
    int y = x;
    while (x!=parent[x])  //持续搜索到根结点
        x = parent[x];  
    int temp;    //此时x为根结点，y为传入结点
    while (y!=x){
         //再次循环，将路径上所有祖先的父结点直接标记为根结点
        temp = parent[y];  
        parent[y] = x;
        y = temp;
    }
    return x;
}

4.union(x,y) 按秩合并

public void union(int x,int y){
     
    link(findSet(x),findSet(y));
}

private void link(int x,int y){
     
    if(rank[x]>rank[y])    //x秩大，y所在的树合并到x所在的树
        parent[y] = x;
    else parent[x] = y;     //x秩不大于y，x所在的树合并到y所在的树
    if (rank[x] == rank[y]){
     
        rank[y]++;
    }
}