一种用于高光谱图像无监督特征提取的超像素PCA方法

SuperPCA：一种用于高光谱图像无监督特征提取的超像素PCA方法

                                        SPCA学习记录

主成分分析（PCA）作为一种无监督的降维方法，已被广泛认为是高光谱图像处理和分析任务的一种有效的预处理步骤。它把每个波段作为一个整体，从全球范围内提取出最具代表性的波段。然而，不同的均匀区域对应着不同的目标，其光谱特征是不同的。对于整个HSI，通过统一投影进行降维显然是不合适的。论文提出了一种简单而有效的超像素PCA方法来学习HSI的低维特征。与经典PCA模型相比，SuperPCA具有四个主要特性。
（1） 与传统的基于整幅图像的PCA方法不同，SuperPCA考虑了不同均匀区域的多样性，即不同的区域应该有不同的投影。
（2） 传统的特征提取模型大多不能直接利用hsi的空间信息，而SuperPCA能够将空间上下文信息融入到超像素分割的无监督降维中。
（3）由于超像素分割得到的区域具有同质性，SuperPCA可以进行提取潜在的低维特征，即使在噪声下。
（4） 虽然SuperPCA是一种无监督的方法，但与有监督方法相比，它可以获得竞争性的性能。由此产生的特征具有区分性、紧凑性和抗噪声性，从而改进了HSI分类性能。在三个公共数据集上的实验表明，SuperPCA模型明显优于传统的基于PCA的HSI降维基线和一些最新的特征提取方法。

高光谱

高光谱图像（HSI）是由星载或机载传感器（如AVIRIS、HyMap、HYDICE和Hyperion）获取的，通常记录图像中每个像素的物质的数十万个光谱波长，这为遥感的许多应用开辟了新的前景。

由于不同的光谱特征可以捕捉到地表覆盖物的细微差异，因此高光谱图像是一种非常适合于鉴别感兴趣物质的技术。虽然丰富的光谱特征可以为数据分析提供有用的信息，但是HSI数据的高维性带来了一些新的挑战：（i）增加了数据传输和存储的负担；（ii）导致维数灾难问题，这将降低分类器的泛化能力并恶化分类性能，特别是当可用的标记样本有限时。

由于（i）光谱波长的密集采样和（ii）大多数材料的光谱反射率仅在特定光谱带上逐渐变化，因此许多相邻波段高度相关，并非所有特征（或光谱带）都有望为手头的数据分类/分析任务提供有用信息。降维作为解决这一问题的典型方法之一，被广泛应用于高维HSI谱空间中的高相关和冗余测量，并在低维子空间中保留基本信息。

特征

从特征提取的角度来说，一般可分为特征选择和特征提取两大类。前者倾向于从原始波段中选择最具代表性的一小部分波段，而后者则旨在寻找一个最佳变换矩阵，将原始高维光谱特征投影到低维子空间特征选择只能从HSI中选择现有波段，而特征提取可以利用整个频带来产生更具区分性的特征。

论文主要研究重点研究利用特征提取来减少特征HSI的尺寸。根据是否使用标签信息，特征提取可分为无监督方法和有监督方法。

传统的方法通常学习单一投影来提取HSI特征。然而，HSI中的不同区域可能对应不同的目标，其光谱特征是不同的。因此，合理的方法是学习不同区域的不同投影矩阵。

图像分割可以看作是将观察到的图像完全分割成许多不同的区域，每个区域都被认为是均匀的。这些区域形成了一个分割图，可以用作光谱空间分类的空间结构。

论文提出了一种简单而有效的基于超像素PCA的无监督特征提取方法。它可以通过对超像素分割得到的每个均匀区域进行PCA来学习HSI数据不同区域的内在低维特征，如图1所示。通过超像素分割，HSI被分割成许多均匀区域，这些区域由矩阵表示，矩阵的列是像素的谱向量。对这些高维矩阵进行主成分分析，得到降维矩阵。最后，对这些低维矩阵进行重新组合，形成降维的hsi。

传统方法通常学习用于HSI特征提取的单一投影[30]、[38]、[39]、[40]。然而，HSI中的不同区域可能对应不同的目标，其光谱特征是不同的。因此，合理的方法是学习不同区域的不同投影矩阵。图像分割可以看作是将观察到的图像完全分割成许多不同的区域，每个区域都被认为是均匀的[41]。这些区域形成了一个分割图，可以用作光谱空间分类的空间结构。

为了充分利用HSI立方体中的空间信息，进一步建立了一种基于多尺度分割的SuperPCA模型MsuperPCA，该模型能够有效地集成多尺度空间信息，通过决策融合得到最优的分类结果。图2演示了我们提出的多尺度超级钙方法的示意图。首先，利用熵率超像素（ESR）方法，根据输入HSI的第一主分量，通过设置不同的超像素数，获得多尺度超像素分段。然后，针对每个尺度，采用基于Superca的无监督降维方法，得到了降维HSIs。在支持向量机（SVM）分类法对不同尺度的预测基础上，通过多数投票决策融合策略生成最终分类结果。

据我们所知，这是第一次采用超像素模型进行高光谱无监督降维和分类图像。广泛实验结果表明，该方法不仅简单直观，与最先进的基于降维的方法（包括最近提出的一些监督特征提取技术）相比，还可以获得最具竞争力的HSI分类结果。当标签信息有限时（少量带标签的培训样本，例如每班5个样本），

提出的SuperPCA和msuperpa方法比最先进的监督特征提取技术获得更好的分类精度。

熵率超像素分割（ERS）

对于一个超像素分割算法，它应该具有以下特点。首先，超级像素应该很好地附着在对象边界上。其次，作为一个预处理过程，超像素分割本身的计算复杂度应该很低。

近年来，基于图结构的分割方法在超像素分割和应用中得到了广泛的应用。一种典型的超像素分割技术是基于特征的归一化割集（NCuts）解。

然而，它需要构造一个非常大的图（G=（V，E）），其顶点（V）是待分割图像中的像素，边缘集（E）由加权函数s:E→R+∪{0}组成。因此，在如此大的相似度矩阵上进行特征值分解是非常耗时的，对于中等大小的图像（例如500×300像素左右）的分割需要几分钟的时间。TurboPixel[45]是实现类似规则性的有效替代方案。然而，它会破坏图像的细节，导致低边界回忆。有人提出了一种ERS分割方法，通过选择边的子集a⊆E将图划分为连通子图，使得得到的图G′=（V，a）由较小的连通分量/子图组成。在ERS的目标函数中，它结合了熵率项H（A）和平衡项B（A），以优化超像素分割：

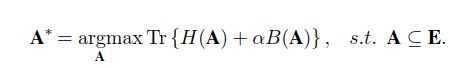
在这里，第一项有利于形成均匀和紧密的团簇，而第二项可以用来鼓励具有相似大小的团簇。α用于平衡熵率项H（A）和平衡项B（A）的贡献。如中所述，贪婪算法有效地解决了优化问题。这种方法效率很高，只需2.5秒就可以分割出500×300像素的图像。 参考文献【46】

SuperPCA

HSI立方体 X∈R^(M×N×L) 由数百个近相邻的光谱带组成，每个像素的光谱分辨率都很高（5-10nm）。这里，M、N和L分别是图像行数、列数和采样波长数。我们可以将三维立方体重塑为一个二维矩阵，X=[x1，x2，···，xP]∈R(L×P)（P=MN），其中每一列代表一个像素向量，反映像素所覆盖的空间区域内材料的能谱。

PCA通过计算在降维空间中使数据方差最大化的低维表示来进行降维。具体地说，它找到了从原始L维空间X∈R^(L×P)到低维空间Y=[y1，y2，···，yP]∈的线性映射 R ^(D×P)，D＜L。在不损失一般性的情况下，我们用W表示变换矩阵，即，Y= W ^T X。数学上，它的目的是通过求解以下目标函数来找到线性变换矩阵，

其中Cov（X）代表数据集X的协方差矩阵，Tr（X）表示n×n平方矩阵X的轨迹。

PCA由于其简单、有效和对噪声的鲁棒性，被广泛应用于许多基于HSI的应用程序的预处理步骤。然而，在HSI中，有许多同质区域。在每个区域内，像素更有可能是同一类。

全局主成分分析和聚类主成分分析结果相似，说明聚类预处理是无效的。这是因为ClusterPCA不使用空间信息，而是将每个像素看作一个独立的数据样本。相比之下，SquarePCA和SuperPCA利用方形面片或超级像素区域内的空间信息，从而获得更好的性能。这种优势在存在噪声的情况下变得更加明显。为了证明这一点，我们将方差为σ=10的加性高斯白噪声（AWGN）添加到原始hsi中。请参考表一的第三块，当加入噪声时，ClusterPCA的性能会急剧下降，而SquarePCA和SuperPCA方法受噪声的影响较小。

PCA由于其简单、有效和对噪声的鲁棒性，被广泛应用于许多基于HSI的应用程序的预处理步骤。然而，在HSI中，有许多同质区域。在每个区域内，像素更有可能是同一类[48]、[49]、[50]、[51]。
全局PCA方法考虑整个数据空间（由HSI立方体的所有像素向量组成），并试图为这个空间找到最佳的变换向量。它可以忽略同质区域的差异。如玩具示例（图3）所示，我们假设数据空间由类1（用蓝色正方形标记）和类别2（用橙色正方形标记）组成，它可能代表了来自两个不同均匀区域的样本分布希斯。我们可以明显看出，类1和类2的转换向量w1和w2显著不同，它们也不同于生成的转换向量w。

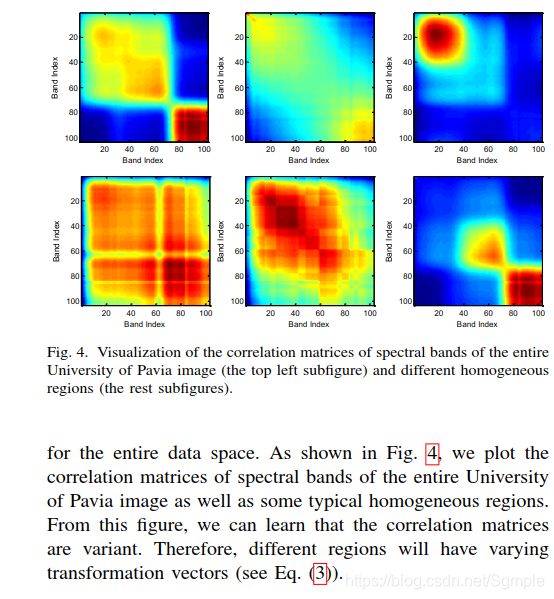
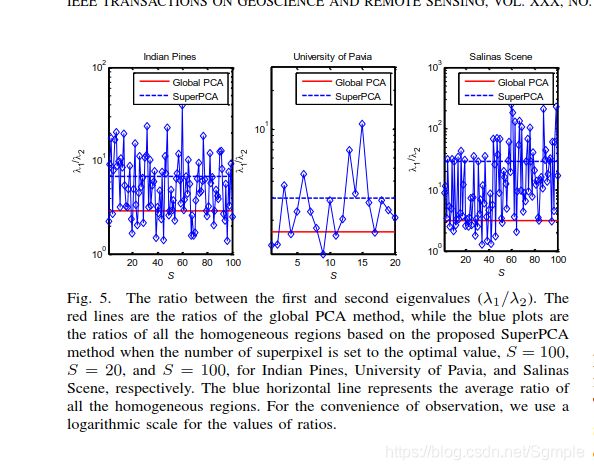
对于整个数据空间。如图4所示，我们绘制了整个帕维亚大学图像光谱带的相关矩阵以及一些典型的均匀区域。

从该图中，我们可以了解到相关矩阵是多样的。因此，不同区域将具有不同的变换向量（见公式（3））。

均匀区域的生成

受上述观察结果的启发，本文提出了一种分而治之的策略来对每个同质区域进行基于PCA的无监督特征提取。通过对每个均匀区域提取相同数量的主成分（PCs），我们可以将它们组合起来形成降维hsi（图2）。接下来，我们将介绍使用超像素分割技术构造均匀区域，它可以将图像彻底分割成许多均匀区域。

与许多基于超像素分割的高光谱图像分类和恢复方法[48]、[49]、[52]、[53]一样，我们采用了ERS，因为它在效率和效率方面都有很好的表现。其他最先进的方法，如简单线性迭代聚类（SLIC）[54]也可以用来代替ERS。特别是，我们首先获得了HSIs的第一个主成分，即获取了高光谱的主要信息。这进一步降低了超像素分割的计算成本。然后，我们对If进行ESR以获得超像素分割，


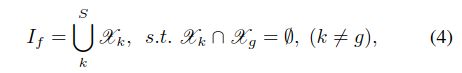
通过将HSI分割为超级混合体，利用有关陆地表面的丰富空间信息是有益的[52]，[32]。然而，在实际应用中，如何为超像素数目选择一个最具挑战性的问题[46]。

当超像素太大时（通过设置一个小的超像素数），产生的欠分割结果会导致标记模糊的边界超像素，需要进一步分割。当超级像素太小（通过设置一个较大的超级像素数），从过分割区域计算的特征可能变得不太明显，从而更难推断出正确的标签。

此外，如文献[55]所述，没有一个区域大小可以充分描述HSI的空间信息。受分类器和决策融合技术[56]、[57]、[58]的启发，本文提出了多尺度分割策略，以提高基于单尺度superca的方法的性能，从而减轻上述问题问题。更多具体来说，主成分图像If（HSIs的第一个主成分）被分割成2C+1层。那个第c级超像素数为Sc，

其中Sf是基本的超像素数，是根据经验设定的。由于Sc的值可能不是{1，2，…，P}中的整数，我们将其重置为Sc=min（max（1；round（Sc））；P）。这里，P是hsi中的总像素数。通过利用多尺度超像素，决策融合策略可以提高分类精度，尤其是在冲突情况下。具体来说，我们融合了由不同的多尺度超像素预测的每个测试像素的标签信息。也就是说，假设将基本图像If分割为2C+1尺度，则HSI将有2C+1不同的分类结果。然后，我们可以通过一个有效的决策融合策略来聚合结果。在本文中，我们利用基于多数投票（MV）的决策融合策略，因为它对不精确的后验概率估计不敏感：

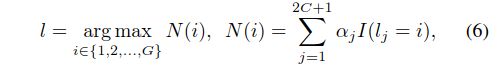
其中，l是测试像素的G个可能类之一的类标签，j是分类索引，N（i）表示类别i在分类库中预测的次数，i表示指示符函数。式（6）中，αj表示第j类的投票权。执行这种自适应投票机制的一种可能方法是根据分类者的信任分数来衡量其投票，该分数可从训练数据中学习。在本文中，我们直接使用等投票强度αj=12c+1（j=1，2，…，2C+1）。

图2显示了用于HSI分类的提议的多尺度SuperCA方法的框架。我们首先得到输入HSI的第一个主成分。然后，基于ESR算法[46]对不同超像素数的图像进行多尺度分割。对于每个尺度，我们对每个同质区域进行PCA降维，并将所有区域合并形成降维hsi。最后，我们将支持向量机分类应用于每一个降维hsi，并通过多数投票将分类结果融合，以预测测试样本的最终标签。

https://blog.csdn.net/weixin_43641241/article/details/89000081?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2_allfirst_rank_v2~rank_v25-3-89000081.nonecase&utm_term=ers%E8%B6%85%E5%83%8F%E7%B4%A0%E5%88%86%E5%89%B2&spm=1000.2123.3001.4430

总结理解：
① 首先进行PCA得到高光谱的第一主成分，随后运用ERS切出均匀区域，进行SPCA得到各个区域的第一主成分，通过设置不同的超像素数量即可得到多尺度超像素。
③ 然后，针对每个尺度，采用超pca得到降维后的图像，运用基于支持向量机(SVM)分类器对不同尺度进行预测。
⑤ 最后采用多数投票决策融合策略生成最终的分类结果

分而治之策略

全局PCA考虑整个数据空间，并寻找该空间的最佳转换向量，他可能会忽略同质区域的差异，如下图中的例子所示，假设数据空间由第1类(蓝色方块)和第2类(橙色方块)构成，这两类可能代表了图像中两个不同均匀区域的样本分布，图中可看出第1类和第2类的变换向量w1和w2是显著不同的，它们也不同于为整个数据空间生成的变换向量w。

这篇文章提出了一种基于超pca的多尺度分割决策融合模型(MSuperPCA)，通过将整个高光谱图像分割成多个不同均匀区域可以更方便的进行降维处理得到图像本质的低维特征空间，通过多尺度融合可以充分利用图像中包含的单尺度无法提取的空间信息。MSuperPCA算法在训练样本有限的情况下，具有明显的优势。另外，该方法继承了传统PCA的优点，在其他高光谱图像的预处理中使用它替换传统PCA方法可能会取得更好的效果