深度学习:正则化-权重衰减-(2). AdamW实现
摘要:第一部分中解释了权重衰减及其现有框架实现的不合理处,这部分从源码出发,在不影响原始Adam优化器使用的情况下添加解耦权重衰减。使用Tensorflow框架。
目录
- Adam源码修改
- 结果对比
主要参考文献
源码的修改根据参考【1】简化。
【1】“https://github.com/OverLordGoldDragon/keras-adamw”
【2】“Decoupled Weight Decay Regularization”
1. Adam源码修改
直接给出修改后的源码,增加行98-106,增加参数wd,wd_dir。
"""From built-in optimizer classes.
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import six
import copy
from six.moves import zip
from keras import backend as K
from keras.utils.generic_utils import serialize_keras_object
from keras.utils.generic_utils import deserialize_keras_object
from keras.legacy import interfaces
from keras.optimizers import Optimizer
class Adam(Optimizer):
"""Adam optimizer.
Default parameters follow those provided in the original paper.
# Arguments
learning_rate: float >= 0. Learning rate.
beta_1: float, 0 < beta < 1. Generally close to 1.
beta_2: float, 0 < beta < 1. Generally close to 1.
amsgrad: boolean. Whether to apply the AMSGrad variant of this
algorithm from the paper "On the Convergence of Adam and
Beyond".
# References
- [Adam - A Method for Stochastic Optimization](
https://arxiv.org/abs/1412.6980v8)
- [On the Convergence of Adam and Beyond](
https://openreview.net/forum?id=ryQu7f-RZ)
"""
def __init__(self, learning_rate=0.001, beta_1=0.9, beta_2=0.999, wd=0.0, wd_dir=None,
amsgrad=False, **kwargs):
self.initial_decay = kwargs.pop('decay', 0.0)
self.epsilon = kwargs.pop('epsilon', K.epsilon())
learning_rate = kwargs.pop('lr', learning_rate)
super(Adam, self).__init__(**kwargs)
with K.name_scope(self.__class__.__name__):
self.iterations = K.variable(0, dtype='int64', name='iterations')
self.learning_rate = K.variable(learning_rate, name='learning_rate')
self.beta_1 = K.variable(beta_1, name='beta_1')
self.beta_2 = K.variable(beta_2, name='beta_2')
self.decay = K.variable(self.initial_decay, name='decay')
self.amsgrad = amsgrad
self.wd = wd
self.wd_dir = wd_dir
@interfaces.legacy_get_updates_support
@K.symbolic
def get_updates(self, loss, params):
grads = self.get_gradients(loss, params)
self.updates = [K.update_add(self.iterations, 1)]
lr = self.learning_rate
if self.initial_decay > 0:
lr = lr * (1. / (1. + self.decay * K.cast(self.iterations,
K.dtype(self.decay))))
t = K.cast(self.iterations, K.floatx()) + 1
lr_t = lr * (K.sqrt(1. - K.pow(self.beta_2, t)) /
(1. - K.pow(self.beta_1, t)))
ms = [K.zeros(K.int_shape(p),
dtype=K.dtype(p),
name='m_' + str(i))
for (i, p) in enumerate(params)]
vs = [K.zeros(K.int_shape(p),
dtype=K.dtype(p),
name='v_' + str(i))
for (i, p) in enumerate(params)]
if self.amsgrad:
vhats = [K.zeros(K.int_shape(p),
dtype=K.dtype(p),
name='vhat_' + str(i))
for (i, p) in enumerate(params)]
else:
vhats = [K.zeros(1, name='vhat_' + str(i))
for i in range(len(params))]
self.weights = [self.iterations] + ms + vs + vhats
for p, g, m, v, vhat in zip(params, grads, ms, vs, vhats):
m_t = (self.beta_1 * m) + (1. - self.beta_1) * g
v_t = (self.beta_2 * v) + (1. - self.beta_2) * K.square(g)
if self.amsgrad:
vhat_t = K.maximum(vhat, v_t)
p_t = p - lr_t * m_t / (K.sqrt(vhat_t) + self.epsilon)
self.updates.append(K.update(vhat, vhat_t))
else:
p_t = p - lr_t * m_t / (K.sqrt(v_t) + self.epsilon)
eta_t = 1.0
if self.wd != 0:
'''Normalized weight decay according to the AdamW paper
'''
if p.name in self.wd_dir.keys():
print(self.wd_dir.keys())
# w_d = self.wd*K.sqrt(self.batch_size/(self.samples_per_epoch*self.epochs))
w_d = self.wd
p_t = p_t - eta_t*(w_d*p)
self.updates.append(K.update(m, m_t))
self.updates.append(K.update(v, v_t))
new_p = p_t
# Apply constraints.
if getattr(p, 'constraint', None) is not None:
new_p = p.constraint(new_p)
self.updates.append(K.update(p, new_p))
return self.updates
def get_config(self):
config = {
'learning_rate': float(K.get_value(self.learning_rate)),
'beta_1': float(K.get_value(self.beta_1)),
'beta_2': float(K.get_value(self.beta_2)),
'decay': float(K.get_value(self.decay)),
'epsilon': self.epsilon,
'amsgrad': self.amsgrad,
'wd': self.wd,
'wd_dir': self.wd_dir}
base_config = super(Adam, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
2. 结果对比
对不加权重衰减,使用 L 2 L_2 L2范数正则化以及使用解耦权重衰减的三种情况进行对比,使用与第一部分内容相同的手工数据。
按照准备数据——选择模型——计算代价函数、梯度,进行训练的顺序进行。
首先准备数据集。
import keras
from keras import layers
import tensorflow as tf
# 准备数据集
num_train, num_test = 20, 100
num_features = 200
true_w, true_b = tf.ones((num_features, 1)) * 0.01, 0.05
features = tf.random.normal((num_train + num_test, num_features))
noises = tf.random.normal((num_train + num_test, 1)) * 0.01
labels = tf.matmul(features, true_w) + tf.convert_to_tensor(true_b) + noises
train_data, test_data = features[:num_train, :], features[num_train:, :]
train_labels, test_labels = labels[:num_train], labels[num_train:]
其次,选择过拟合的模型,模型中设置 L 2 L_2 L2正则化为0。
# 选择模型
model = keras.models.Sequential([
layers.Dense(units=128, activation='relu', input_dim=200),
layers.Dense(128, activation='relu', kernel_regularizer=keras.regularizers.l2(0.00)),
layers.Dense(1)
])
model.summary()
计算代价函数、梯度,进行训练。
Adam的使用方式和原来稍有不同,需要查找网络中包含 L 2 L_2 L2正则化的层,然后对这些层的参数进行权重衰减。
首先是无 L 2 L_2 L2正则化,无权重衰减的情况。
weight_decays_dir = get_weight_decays(model)
adam = Adam(learning_rate=0.001, wd=0.00, wd_dir=weight_decays_dir)
model.compile(optimizer=adam,
loss='mse',
metrics=['mse'])
hist1 = model.fit(train_data, train_labels, steps_per_epoch=2, epochs=100, validation_steps=1,validation_data=[test_data, test_labels])
修改网络中的 L 2 L_2 L2正则化,得到仅包含 L 2 L_2 L2正则化的结果。
修改wd的值,得到仅包含权重衰减的结果。
结果如下:
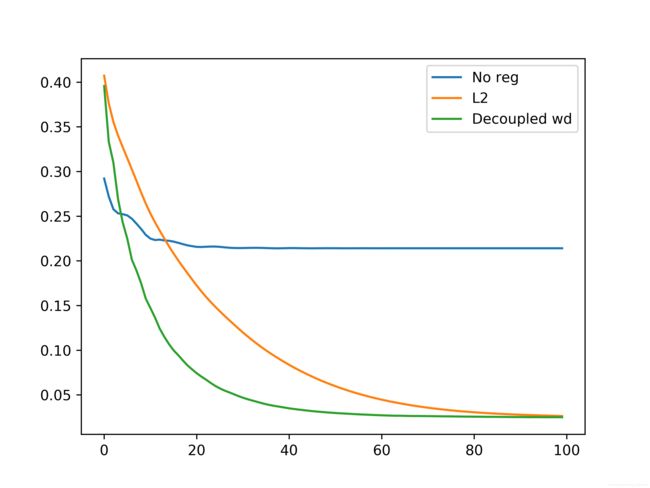
可以看到,解耦权重衰减和 L 2 L_2 L2正则化在Adam中有不同的结果。这里虽然两者最终取得了一样的结果,但根据【2】作者的结果,解耦权重衰减能使权重衰减超参数的选择独立于学习率,简化优化难度,且泛化能力更强。