基于PSO算法的无线传感器网络的覆盖优化

一、理论基础

1、节点感知模型

传感器节点的感知模型主要分为两种：0/1(二元)感知模型和概率感知模型。

（1）0/1感知模型

该模型是最理想的感知模型，指的是在一个平面上以传感器节点为圆心、$r$为半径的圆区域，在此区域内的感知概率记为1，超出这个区域的传感器对它的感知概率为0。其中$r$感知半径由传感器节点的物理特性决定。对二维平面的任何一定点$p(x,y)$，传感器节点$i$对它的感知概率定义如下：$$p=\{\begin{array}{l}1,if{d}_{ip}\le r\\ 0else\end{array}\text{\hspace{1em}(1)}$$上式中$r$是传感器的感知半径，$d_{ip}$是传感器节点到目标点$p$的欧氏距离。$$d_{ip}=\sqrt{(x-x_i{)}^2+(y-y_i{)}^2}\text{\hspace{1em}(2)}$$二元感知模型推广到三维空间中，就是以传感器节点为圆心、半径为感知半径$rs$的球形区域。

（2）概率感知模型

由于实际的无线传感器网络的应用环境非常的复杂，节点的感知能力会随着距离的增大而减弱，概率感知模型解决了这个问题。传感器节点$i$对平面内任何一点$p(x,y)$的感知概率为：$$p=e^{-\alpha d_{ip}}\text{\hspace{1em}(3)}$$$dip$指的是传感器节点$i$到$p$点的距离；参数$\alpha$指的是节点随着距离的增大感知能力的衰减程度。后来 Zou 等对这个模型进行了修改，使之更加适合于实际环境的感知。当目标点到传感器节点的距离小于$r-r_e$的时候，传感器节点对该目标点的感知概率为 1，当目标点到传感器节点的距离大于$r+r_e$的时候，传感器节点对该目标点的感知概率为 0，在两者之间的时候，感知能力为两点距离的指数函数，具体描述如下：$$p=\{\begin{array}{l}0,r+r_e<d_{ip}\\ e^{-\lambda {\alpha }^{\beta }},r-r_e<d_{ip}<r+r_e\\ 1,r-r_e\ge d_{ip}\end{array}\text{\hspace{1em}(4)}$$其中，$r_e$为传感器节点不确定检测能力的一个度量。参数$\alpha =d_{ip}-(r-r_e)$，$\lambda$和$\beta$用于刻画当目标点$p$和传感器节点$i$之间的距离落于某个测量范围之内时，传感器节点$i$对目标点$p$的感知概率。
本文主要基于0/1模型，进行寻优。

2、覆盖数学模型

现假定目标监测区域为二维平面，在区域$Area$上投放同型结构传感器节点的数目为$N$，每个节点的位置坐标值假设已被初始化赋值，且节点的感知半径为$r$。传感器节点集则表示为：$$Node\{x_1,x_2,\cdots ,x_N\}\text{\hspace{1em}(5)}$$其中$nod{e}_i=\{x_i,y_i,r\}$，表示以节点$(x_i,y_i)$为圆心，$r$为监测半径的圆，假定监测区域$Area$被数字化离散为$l\times m$个像素点，像素点的坐标为$(x,y)$，目标像素点与传感器节点间的距离为：$$d(nod{e}_i,p)=\sqrt{(x_i-x{)}^2+(y_i-y{)}^2}\text{\hspace{1em}(6)}$$目标区域内像素点被传感器节点所覆盖的事件定义为$c_i$。则该事件发生的概率$P{c}_i$即为像素点$(x,y)$被传感器节点$nod{e}_i$所覆盖的概率:$$P_{cov}(x,y,nod{e}_i)=\{\begin{array}{l}1,ifd(nod{e}_i,p)\le r\\ 0,otherwise\end{array}\text{\hspace{1em}(7)}$$我们将所有的传感器节点$Node$在目标监测环境中的区域覆盖率$R_{area}(node)$定义为传感器节点集$Node$的覆盖面积与监测区域的面积$Area$之比，如公式(8)所示：$$R_{area}(node)=\frac{\sum P_{cov}}{Area}\text{\hspace{1em}(8)}$$那我们的最终目标就是找到一组节点使得覆盖率最大。

3、粒子群优化(PSO)算法

请参考这里。

二、MATLAB程序实现

1、参数设置

实验参数：
迭代次数：400，节点个数：20，感知半径：$r=3$，位置范围：$[0,20]$，速度范围：$[-2,2]$，加速因子：$c_1=c_2=1.4926$，惯性权重：$0.5<wg<0.9$，离散粒度：$data=1$

2、适应度函数

适应度函数fun.m代码如下：

function z = fun(x, y, L, R, data)
%% 适应度函数：WSN的覆盖率
% input：
% x        圆心横坐标
% y        圆心纵坐标
% L        区域边长
% R        通信半径
% data     离散粒度
% output:
% z        覆盖率
N = length(x);                      % 节点总个数
[m, n] = meshgrid(1:data:L);        % 离散化区域内的点
[row, col] = size(m);
for i = 1:N
    D = sqrt((m-x(i)).^2+(n-y(i)).^2);   % 计算坐标点到圆心的距离
    [m0, n0] = find(D <= R);             % 检测出圆覆盖点的坐标
    Ind = (m0-1).*col+n0;                % 坐标与索引转化
    M(Ind) = 1;                          % 改变覆盖状态
end
scale = sum(M(1:end))/(row*col);         % 计算覆盖比例
z = scale;

3、主函数

%% 清空环境变量
clc
clear
%% 网络参数
L = 20;                  % 区域边长
n = 20;                  % 节点个数
R = 3;                   % 通信半径
data = 1;                % 离散粒度
%% 粒子群参数
maxgen = 400;            % 迭代次数
sizepop = 30;            % 粒子规模
Wmax = 0.9;
Wmin = 0.5;
%% 参数初始化
c1 = 1.4926;             % 自我认知参数
c2 = 1.4926;             % 社会认知参数
Vmax = 2;                % 最大速度
Vmin = -2;               % 最小速度
popmax = 20;             % 位置最大值
popmin = 0;              % 位置最小值
gbest = zeros(sizepop, 2);  % 最优解
%% 随机生成群体位置、速度和对应的适应度值
empty_pop.Position = [];
empty_pop.V = [];
pop = repmat(empty_pop, sizepop, 1);
for i=1:sizepop
    pop(i).Position = rand(n, 2).*[L, L];  % 初始种群位置
    pop(i).V = rands(n, 2)*2;              % 初始化速度
    fitness(i) = fun(pop(i).Position(:, 1), pop(i).Position(:, 2), L, R, data);  % 粒子群的适应度
end
[bestfitness, bestindex] = max(fitness);
gbest = pop(bestindex).Position;    % 群体最优极值
pbest = pop;                        % 个体最优极值
fitnessgbest = bestfitness;         % 种群最优适应度值
fitnesspbest = fitness;             % 个体最优适应度值
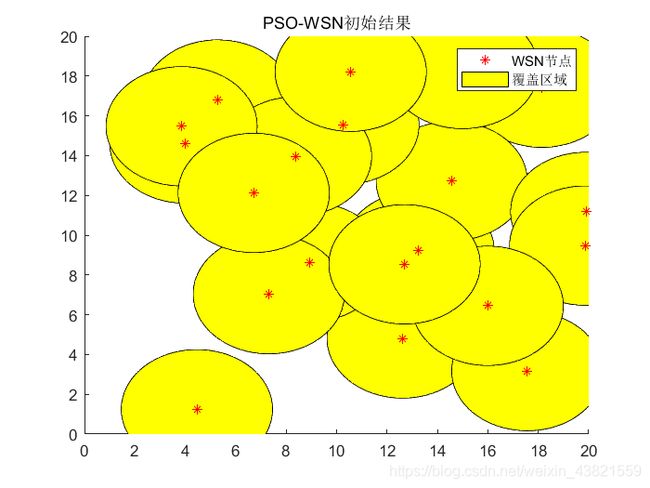
%% 初始结果显示
disp('初始位置：' );
disp([num2str(gbest)]);
disp(['初始覆盖率：', num2str(fitnessgbest)]);
% 初始覆盖图
figure
for i = 1:n
    axis([0 L 0 L]);        % 限制坐标范围
    x = gbest(:, 1);
    y = gbest(:, 2);
    sita = 0:pi/100:2*pi;   % 角度[0, 2*pi]
    hold on;
    p2 = fill(x(i)+R*cos(sita), y(i)+R*sin(sita), 'y');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
     'WSN节点', '覆盖区域'});
title 'PSO-WSN初始结果';
%% 迭代寻优
for i = 1:maxgen
    W = Wmax-((Wmax-Wmin)/maxgen)*i;
    for j=1:sizepop
        %% 速度更新
        pop(j).V = W*pop(j).V + c1*rand*(pbest(j).Position - pop(j).Position) + c2*rand*(gbest - pop(j).Position);
        % 边界处理
        pop(j).V = max(pop(j).V, Vmin);
        pop(j).V = min(pop(j).V, Vmax);
        %% 位置更新
        pop(j).Position = pop(j).Position+pop(j).V;
        % 边界处理
        pop(j).Position = max(pop(j).Position, popmin);
        pop(j).Position = min(pop(j).Position, popmax);
        %% 适应度值更新
        fitness(j) = fun(pop(j).Position(:, 1), pop(j).Position(:, 2), L, R, data);    
    end
    %% 个体和群体极值更新
    for j = 1:sizepop
        % 个体极值更新
        if fitness(j) > fitnesspbest(j)
            pbest(j).Position = pop(j).Position;
            fitnesspbest(j) = fitness(j);
        end
        % 群体极值更新
        if fitness(j) > fitnessgbest
            gbest = pop(j).Position;
            fitnessgbest = fitness(j);
        end
    end
    %% 每一代群体最优值存入zz数组
    zz(i) = fitnessgbest;
end
%% 结果显示
disp('最优位置：' );
disp([num2str(gbest)]);
disp(['最优覆盖率：', num2str(zz(end))]);
%% 绘图
figure;
plot(zz, 'r', 'lineWidth', 2);          %  画出迭代图
title('算法训练过程', 'fontsize', 12);
xlabel('迭代次数', 'fontsize', 12);
ylabel('粒子覆盖率', 'fontsize', 12);
figure
for i = 1:n
    axis([0 L 0 L]);        % 限制坐标范围
    x = gbest(:, 1);
    y = gbest(:, 2);
    sita = 0:pi/100:2*pi;   % 角度[0, 2*pi]
    hold on;
    p2 = fill(x(i)+R*cos(sita), y(i)+R*sin(sita), 'g');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
     'WSN节点', '覆盖区域'});
title 'PSO-WSN最终结果';

3、结果分析

初始随机值和最终的最优解如下：

初始位置：
18.1426      17.4146
12.6183      4.80828
13.2471      9.23198
3.99968      14.6056
14.5673      12.7206
10.2703      15.5448
4.45868      1.24848
15.0005      18.3539
5.28778      16.8189
8.93886      8.64458
19.9012      11.1719
7.31079      7.03445
8.38784      13.9555
19.8618      9.47548
3.85099      15.4728
17.5644      3.16575
10.5605      18.2156
15.9934      6.44904
6.71419      12.1231
12.6944       8.5344
初始覆盖率：0.7925
最优位置：
19.4637      14.7853
13.4154      19.1361
3.46777      18.9849
6.46746      12.4126
7.52069      16.4914
 13.162      10.0433
17.7051      9.21258
14.5105      3.48361
19.9587      5.85257
10.4474     0.398281
11.1843      15.0086
7.94295      5.75535
8.84837      8.54376
13.3125      4.73947
15.5737      14.7703
2.01602      15.1003
2.71127      8.70626
3.29044       3.1522
 17.601      1.09552
3.57696      11.8814
最优覆盖率：0.9425

对应的覆盖图如图1、图2所示。

图1 PSO-WSN初始覆盖效果

图2 PSO-WSN最终覆盖效果

覆盖率变化如图3所示。

图3 WSN节点覆盖率变化

三、参考文献

[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D].南京理工大学,2013.
[2] 张谦. 基于群智能算法的无线传感器网络覆盖优化研究[D].湖南大学,2015.
[3] ~心升明月~. 基于粒子群优化算法的函数寻优算法. CSDN博客.