数字图像分割（一）：不连续性分割——边缘检测
目录
一阶导算子：
最简单的算子
需要注意的点：
1.same padding
2.x,y方向的梯度差异
3.未加阈值
其他的算子
Roberts[1965]
Prewitt[1970]
Sobel[1970]
这些核之间的区别：
二阶算子
一阶导与二阶导的区别
Laplace算子
噪声影响
Canny边缘检测
常规检测区别
过程
非极大值抑制
设置高低阈值
Canny整体流程
一阶导算子：
前向差分：
反向差分：
中心差分：
最简单的算子
下面是关于一个最简单的前向/后向一阶导：
kernel_x = [-1,1]
kernel_y = [-1,1]
自己写的一段程序，执行方式为：
在文件所在终端执行命令：python SimpleKernel.py 图片路径
"""
name:SimpleKernel.py
run:python SimpleKernel.py path_of_your_img
"""
import numpy as np
import sys
import os
from PIL import Image
# define simple kernel
simple_kernel_x = np.array([-1,1])
simple_kernel_y = np.array([-1,1])
def read_img(path):
"""
path: input img path
return: gray img
"""
img = Image.open(path)
img_gray = img.convert("L")
return img_gray
def pad_img(img):
"""
img:type of PIL
"""
# transform to ndarray
img_array = np.array(img, dtype=np.uint8)
# get length and width
length = img_array.shape[0]
width = img_array.shape[1]
padding_x = np.zeros((length,1))
padding_y = np.zeros(width+1)
img_pad = np.hstack((img_array, padding_x))
img_pad = np.vstack((img_pad, padding_y))
img_save("img_pad.png", img_pad)
return img_pad, length, width, img_pad.shape[0], img_pad.shape[1]
def simple_convolute(img_pad, simple_kernel_x, simple_kernel_y):
"""
compute the directional edge of img
"""
x_list = []
y_list = []
for i in range(img_pad.shape[0]-1):
for j in range(img_pad.shape[1]-1):
# x grad
cut_x = img_pad[i,j:j+2]
grad_x = (simple_kernel_x*cut_x).sum()
x_list.append(grad_x)
# y grad
cut_y = img_pad[i:i+2,j]
grad_y = (simple_kernel_y*cut_y).sum()
y_list.append(grad_y)
return x_list, y_list
def img_save(name, img_array):
img_pil = Image.fromarray(img_array)
img_pil = img_pil.convert("RGB")
path_0, path_1 = os.path.split(sys.argv[1])
path_2, _ = os.path.splitext(path_1)
img_pil.save(path_0+path_2+"_"+name)
print("Save img success!")
if __name__ == "__main__":
if len(sys.argv) < 2:
print(__doc__)
exit(1)
img = read_img(sys.argv[1])
img_pad, length, width, length_pad, width_pad= pad_img(img)
print("Original length:{}\nOriginal width:{}".format(length, width))
print("Pad length:{}\nPad wodth:{}".format(length_pad, width_pad))
x_list, y_list = simple_convolute(img_pad, simple_kernel_x, simple_kernel_y)
img_grad_x = np.array(x_list).reshape((length, width))
img_grad_y = np.array(y_list).reshape((length, width))
print(img_grad_x.shape)
print(img_grad_y.shape)
img_save("img_grad_x.png", img_grad_x)
img_save("img_grad_y.png", img_grad_y)
img_grad_all = img_grad_x + img_grad_y
img_save("img_grad_all.png", img_grad_all)执行的效果：
origion image
padding and gray image
x_grad image
y_grad image
all_grad image
需要注意的点：
1.same padding
采用same padding,根据kernel的大小进行补边，代码中的padding 写死了，只补了一行一列，可以根据具体的kernel进行传参修改。
（效果在padding and gray image 中，仔细观察，在图的最右列，最下行，分别多了一全为0的黑边像素。）
2.x,y方向的梯度差异
x_grad image,求x方向的梯度，横向的边缘特征更加明显，与之对应的，y_grad image是y方向的梯度，不过在求梯度值的时候，采取unit8(保存时处理)
下面是另一个角度：
x_grad image uint8
y_grad image uint8
all_grad image unit8
x,y方向上的梯度求解差别，可以细微的观察出来（如果其他图片，效果可能会更好）
3.未加阈值
梯度未加阈值，所有的梯度都显示了出来，所以从unit8上图看，更像是月球的表面，显得坑坑洼洼，高低不平，越亮的地方，表示梯度差别越大。而具有边缘特征的一些像素点则组成了圆圆的边界。如果，加上阈值，则会显示的更加完美。
其他的算子
上面的算子是最简单的算子，每个算子只有两个元素（前向、后向），现在要将算子做扩充：变换成卷积核的形式——3*3
Roberts[1965]
在变成3*3前，还有一个Roberts[1965]算子，是最早检测对角性质的二维检测核。
135° and 45°
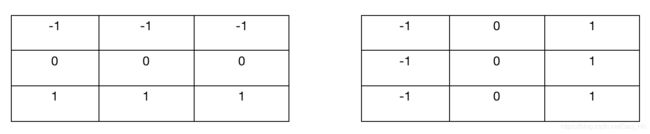
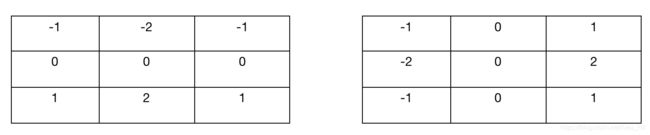
Prewitt[1970]
Prewitt(y,x)
Sobel[1970]
Sobel(y,x)
这些核之间的区别：
1.2*2不是关于中心对称的，3*3是关于中心对称的，3*3带有更多更丰富的边缘信息
2.Sobel相对Prewitt，为梯度算子的中心系数添加了权值，事实证明中心位置使用2可以平滑图像
Prewitt实现相对简单，Sobel具有更好的噪声抑制效果。
对于边缘检测来讲，噪声抑制对分割效果起到了很重要的作用。
二阶算子
有一阶算子就可能检测出一些边缘了，那要二阶导干嘛？
一阶导与二阶导的区别
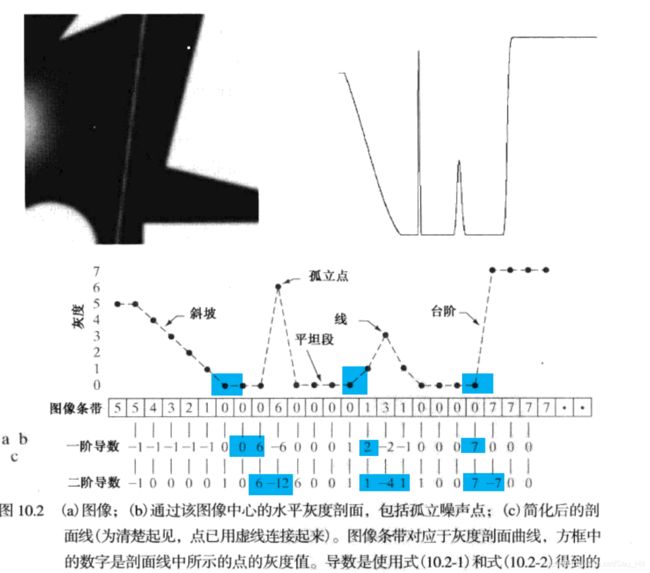
下面展示一副图像，来自论文：Eficient Graph-Based Image Segmentation
这幅图像大致分为三个区域，左侧灰度值连续升高，属于斜坡梯度，右侧有较为明显的台阶梯度。
如果对这幅图像进行一节求导，会发生什么？
图像左半部分的一阶导：恒为a
图像有半部分的一阶导：0,b,0,-b,0
就有这么几个阶段。
右半边一阶导表示还好，但是左半边梯度值恒定，无论是边缘检测还是阈值处理，这都是一个麻烦，怎么设置一个边界进行划分？
下面看一张图：
数字图像处理（冈萨雷斯）
二阶导的作用是什么？
是对导数求导，也就是：变化率的变化率——增长速度。
二阶导大于0：变化率升高
二阶导小于0：变化率降低
一阶导的效应：在灰度变化的过程中，求得的是灰度值的斜坡特性，在斜坡两端处阶跃，在斜坡上恒定
二阶导效应：斜坡两端阶跃，且符号不同，在斜坡上恒为0
于是二阶导对于有灰度值变化的阶梯处（斜坡两端），就会出现“双边效应”，如图：
也就是说，在斜坡表征方面，一阶导表征的是条恒定的宽边，而二阶导表征的是两条细边，而且二阶导的数值的正负分别表示了图像是从暗到亮，还是从亮到暗。
Laplace算子
二阶导：
中心差分：
偏x差分：
偏y差分:
对于x，y方向的梯度求和，本应用平方差公式求和，但可近似等于GRAD = |X|+|Y|
于是：
Laplace算子（基础，扩展）
代码如下（可直接由上更改、配合使用）：
import numpy as np
import PIL.Image as Image
import sys
import os
from SimpleKernel import read_img
from SimpleKernel import img_save
Laplace_Kernel = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]])
def pad_img(img_gray):
"""
img:type of PIL
"""
# transform to ndarray
img_array = np.array(img_gray, dtype=np.uint8)
# get length and width
length = img_array.shape[0]
width = img_array.shape[1]
padding_x = np.zeros((length,1))
padding_y = np.zeros(width+2)
img_pad = np.hstack((img_array, padding_x))
img_pad = np.hstack((padding_x, img_pad))
img_pad = np.vstack((img_pad, padding_y))
img_pad = np.vstack((padding_y, img_pad))
img_save("pad.png", img_pad)
return img_pad, length, width, img_pad.shape[0], img_pad.shape[1]
def laplace_convolute(img_pad, Laplace_Kernel):
grad_list = []
for i in range(img_pad.shape[0]-2):
for j in range(img_pad.shape[1]-2):
cut = np.array(img_pad[i:i+3,j:j+3]).reshape(3, 3)
# print(cut)
grad = (cut*Laplace_Kernel).sum()
grad_list.append(grad)
return grad_list
if __name__ == "__main__":
# read img and gray
img_gray = read_img(sys.argv[1])
# padding 1 + x + 1/ 1 + y + 1
img_pad, length, width, length_pad, width_pad = pad_img(img_gray)
print("Original length:{}\nOriginal width:{}".format(length, width))
print("Pad length:{}\nPad wodth:{}".format(length_pad, width_pad))
grad_list = laplace_convolute(img_pad, Laplace_Kernel)
img_grad = np.array(grad_list).reshape((length, width))
img_save("grad.png", img_grad)
效果如下：
origion image
padding iamge
Laplace grad image
下面，我们来对比下，最简单的算子检测与Laplace算子检测的区别：
这里均没做阈值处理！
1.左上角的那个球，印证了Laplace双边效应。
2.一阶导线更宽（斜坡），二阶导线更细（阶跃）
3.3*3核比2*2核能够检测到更多的边缘信息
4.Laplace左与上方的白边为padding的0梯度显示（可以自己设定padding以及convolution的方式，这里直接从左上角0,0开始，图像整体向右下角移动1Pixel）
5.对于噪声点/异常点，Laplace非常敏感。如果图像中含有噪声，那么对于二阶导的Laplace来讲，将会出现很多梯度爆炸的极值点。
噪声影响
既然说到了噪声对边缘检测的影响，那么，就顺带提一下。
数字图像处理（冈萨雷斯）
第一行：标准图像：纯黑-斜坡-纯白
第一行的波形显示是理想 状态下的灰度值变化情况。
第二行：加入0.1灰度级的高斯噪声
一阶导，局部变化较缓，阈值界限明显
二阶导，局部变化剧烈，阈值界限可判断
第三行：加入1灰度级的高斯噪声
一阶导：整体的界限还能分辨出，阈值界限可判断
二阶导：明确的双边效应已经消失，阈值界限消失
第四行：加入10灰度级的高斯噪声
一阶导：噪声过大
二阶导：噪声过大
过多的就不多叙述了，在边缘检测之前，尽量要先做消除噪声的操作，比如说高斯模糊等。
Canny边缘检测
常规检测区别
在常规的边缘检测中，在阈值方面，容易出现“高不成低不就”的情况。
也就是说，如果阈值设置的较低，则会出现过多的零碎、杂乱的噪声边界，没有一个清晰地整体边缘。
如果阈值设置的较高，则有可能想要的一些细节性的边缘又检测不到。
针对于这种情况，Canny[1986]边缘检测就出现了。（迄今为止最好的边缘算子检测）
每个点上的梯度可以进行向量化处理，基于x方向与y方向的梯度值，得到该点的梯度方向。(dy/dx)
Canny做了一件什么事情呢？
过程
下面，就来具体的阐述下原理与过程：
1.梯度方向的区域划分
如上图所示，(x,y)点的梯度方向属于哪个范围，就落在哪一类，就分为了8（4）个方向。
我们求完了所有的梯度值与梯度方向后，就需要对这些梯度进行筛选。
非极大值抑制
上面求到的梯度与一般梯度一样，不同的是有梯度方向与之对应。
且在一些局部边缘处，含有极大值周围的宽脊区域，对于我们来讲，我们更需要检测到更细，更精准的线，即：极大值
于是，我们需要在点x,y附近寻找极大值，判断的标准就是上面刚刚划分好的方向区域。
若x,y梯度属于45°~67.5°方向，则在相邻的点（1~2个）中，寻找这个方向的极大值。如果x,y已经属于最大，那么保持不变，如果小于某个梯度值，那么置为0.
设置高低阈值
处理好局部极大值后，我们得到了整体的局部最大值，但这仍然会存在一个问题，细节边缘的连续性。
边缘处可能存在低值边缘梯度，是边缘中的细节部分，这部分极有可能与高值部分脱节、断续，这个时候需要设置低阈值来保证细节部分的保留。
当然，这里有一个前提，并不是所有的低值部分都能保留——与高值边缘连通的低值部分
另一方面，如果太低了，就可以直接抛弃了。
高低阈值比例建议：2：1，3：1
Canny整体流程
另外，Canny是用Sobel算子实现的。
这里用opencv实现一下:
from cv2 import cv2 as cv
import sys
import os
import numpy as np
def save_img(name, img):
path_0, path_1 = os.path.split(sys.argv[1])
path_2, _ = os.path.splitext(path_1)
cv.imwrite(path_0+path_2+"_"+name, img)
if __name__ == "__main__":
# read
img = cv.imread(sys.argv[1], 0)
# Threshold
low_threshold = 30
high_threshold = 100
img_gaussian= cv.GaussianBlur(img, (5,5), 1)
img_canny = cv.Canny(img_gaussian, low_threshold, high_threshold)
save_img("grad.png", img_canny)
阈值处理后的结果：
canny（30，100）
边缘检测的部分先写到这里，后续不足继续更新。
下一篇写下基于阈值的分割方法。