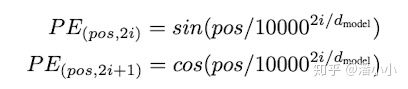transformer模型_【经典精读】Transformer模型深度解读

文字长度: ★★★★★

阅读难度: ★★☆☆☆

原创程度: ★★★★☆

---

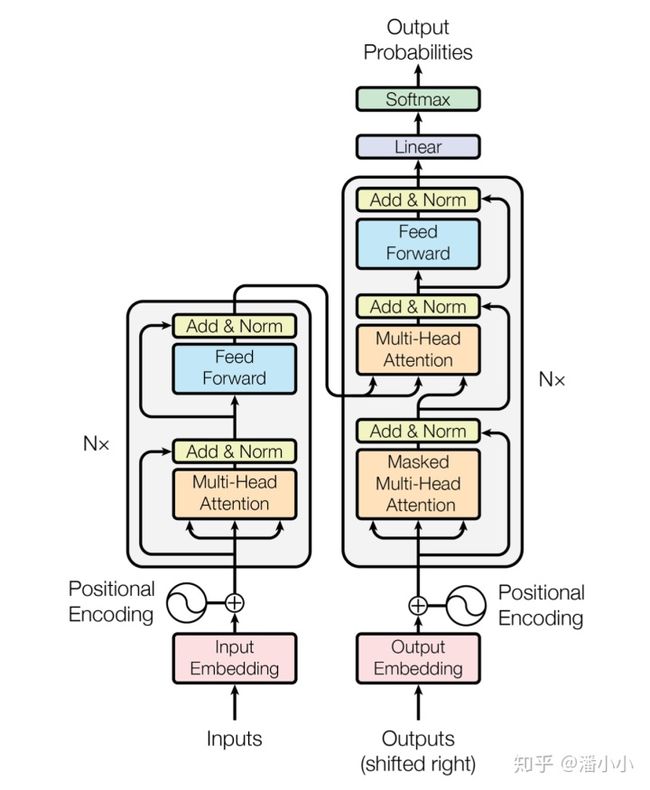
Transformer是2017年的一篇论文《Attention is All You Need》提出的一种模型架构，这篇论文里只针对机器翻译这一种场景做了实验，全面击败了当时的SOTA，并且由于encoder端是并行计算的，训练的时间被大大缩短了。

它开创性的思想，颠覆了以往序列建模和RNN划等号的思路，现在被广泛应用于NLP的各个领域。目前在NLP各业务全面开花的语言模型如GPT, BERT等，都是基于Transformer模型。因此弄清楚Transformer模型内部的每一个细节就显得尤为重要。

鉴于写Transformer的中英文各类文章非常之多，一些重复的、浅显的东西在本文里都不再赘述。在本文中，我会尽可能地去找一些很核心也很细节的点去剖析，并且将细节和整体的作用联系起来解释。

本文尽量做到深入浅出，力求覆盖我自己学习时的每一个困惑，做到“知其然，且知其所以然”。我相信通过我抽丝剥茧的分析，大家会对Transformer每个部分的作用有一个更加深入的认识，从而对这个模型架构整体的认知上升到一个新的台阶，并且能够深刻理解Transformer及其延伸工作的动机。

本文将按照下面的思路展开

0. Transformer整体架构

1. Attention的背景溯源(为什么要有attention?)
2. Attention的细节(attention是什么?)
   1. Query, Key, Value
   2. Multi-head Attention的本质
3. Transformer模型架构中的其他部分
   1. Feed Forward Network
   2. Positional Embedding
   3. Layer Normalization
4. Transformer和RNN的对比
5. 参考

---

0. Transformer架构

Transformer模型的架构

这里就不啰嗦encoder, decoder各自的含义以及模块了，直戳细节。以下将会重点解答的问题有:

• Attention是如何发挥作用的，其中的参数的含义和作用是什么，反向传播算法如何更新其中参数，又是如何影响其他参数的更新的？
• 为什么要用scaled attention？
• Multi-head attention相比single head attention为什么更加work，其本质上做了一件什么事？从反向传播算法的角度分析？
• Positional encoding是如何发挥作用的，应用反向传播算法时是如何影响到其他参数的更新的？同样的理论可以延伸到其他additional embedding，比如多语言模型中的language embedding
• 每个encoder/decoder layer中feed-forward部分的作用，并且从反向传播算法角度分析？
• decoder中mask后反向传播算法过程细节，如何保证training和inference的一致性？
  • 如果不一致（decoder不用mask）会怎么样?

1. Attention的背景溯源

想要深度理解Attention机制，就需要了解一下它产生的背景、在哪类问题下产生，以及最初是为了解决什么问题而产生。

首先回顾一下机器翻译领域的模型演进历史：

机器翻译是从RNN开始跨入神经网络机器翻译时代的，几个比较重要的阶段分别是: Simple RNN, Contextualize RNN, Contextualized RNN with attention, Transformer(2017)，下面来一一介绍。

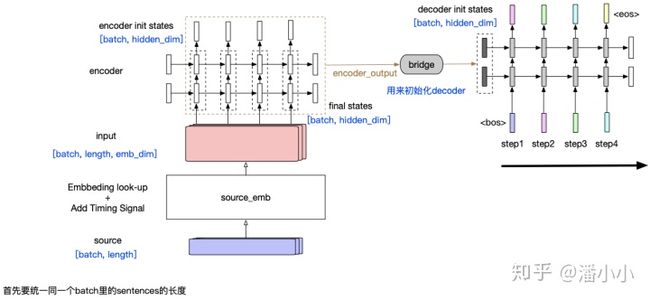
• Simple RNN：这个encoder-decoder模型结构中，encoder将整个源端序列(不论长度)压缩成一个向量(encoder output)，源端信息和decoder之间唯一的联系只是: encoder output会作为decoder的initial states的输入。这样带来一个显而易见的问题就是，随着decoder长度的增加，encoder output的信息会衰减。

Simple RNN (without context)

这种模型有2个主要的问题:

1. 源端序列不论长短，都被统一压缩成一个固定维度的向量，并且显而易见的是这个向量中包含的信息中，关于源端序列末尾的token的信息更多，而如果序列很长，最终可能基本上“遗忘”了序列开头的token的信息。
2. 第二个问题同样由RNN的特性造成: 随着decoder timestep的信息的增加，initial hidden states中包含的encoder output相关信息也会衰减，decoder会逐渐“遗忘”源端序列的信息，而更多地关注目标序列中在该timestep之前的token的信息。

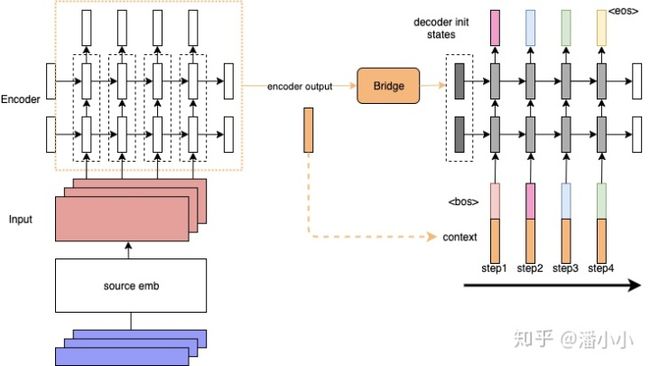
• Contextualized RNN：为了解决上述第二个问题，即encoder output随着decoder timestep增加而信息衰减的问题，有人提出了一种加了context的RNN sequence to sequence模型：decoder在每个timestep的input上都会加上一个context。为了方便理解，我们可以把这看作是encoded source sentence。这样就可以在decoder的每一步，都把源端的整个句子的信息和target端当前的token一起输入到RNN中，防止源端的context信息随着timestep的增长而衰减。

Contextualized RNN

但是这样依然有一个问题: context对于每个timestep都是静态的(encoder端的final hidden states，或者是所有timestep的output的平均值)。但是每个decoder端的token在解码时用到的context真的应该是一样的吗？在这样的背景下，Attention就应运而生了:

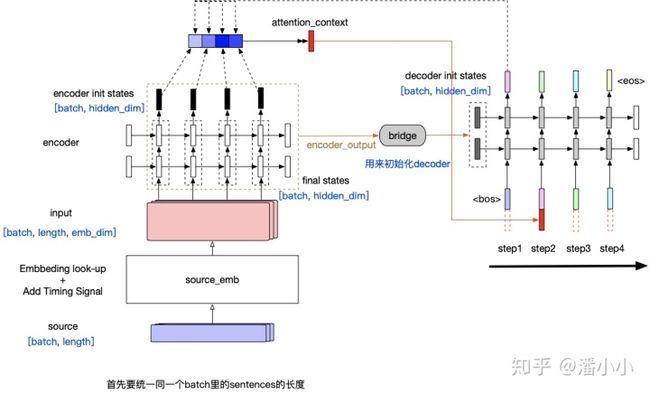
• Contextualized RNN with soft align (Attention) : Attention在机器翻译领域的应用最早的提出来自于2014年的一篇论文 Neural Machine Translation by Jointly Learning to Align and Translate

Contextualized RNN with Attention

在每个timestep输入到decoder RNN结构中之前，会用当前的输入token的vector与encoder output中的每一个position的vector作一个"attention"操作，这个"attention"操作的目的就是计算当前token与每个position之间的"相关度"，从而决定每个position的vector在最终该timestep的context中占的比重有多少。最终的context即encoder output每个位置vector表达的加权平均。

context的计算公式

2. Attention的细节

2.1. 点积attention

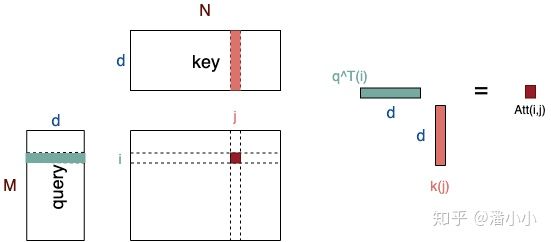
我们来介绍一下attention的具体计算方式。attention可以有很多种计算方式: 加性attention、点积attention，还有带参数的计算方式。着重介绍一下点积attention的公式:

Attention中(Q^T)*K矩阵计算，query和key的维度要保持一致

如上图所示，

,

分别是query和key，其中，query可以看作M个维度为d的向量(长度为M的sequence的向量表达)拼接而成，key可以看作N个维度为d的向量(长度为N的sequence的向量表达)拼接而成。

• 【一个小问题】为什么有缩放因子
  ?
  • 先一句话回答这个问题: 缩放因子的作用是归一化。
  • 假设
    ,
    里的元素的均值为0，方差为1，那么
    中元素的均值为0，方差为d. 当d变得很大时，
    中的元素的方差也会变得很大，如果
    中的元素方差很大，那么
    的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。总结一下就是
    的分布会和d有关。因此
    中每一个元素乘上
    后，方差又变为1。这使得
    的分布“陡峭”程度与d解耦，从而使得训练过程中梯度值保持稳定。

2.2. Attention机制涉及到的参数

一个完整的attention层涉及到的参数有:

• 把
  ,
  ,
  分别映射到
  ,
  ,
  的线性变换矩阵
  (
  ),
  (
  ),
  (
  )
• 把输出的表达
  映射为最终输出
  的线性变换矩阵
  (
  )

2.3. Query, Key, Value

Query和Key作用得到的attention权值作用到Value上。因此它们之间的关系是:

1. Query
   和Key
   的维度必须一致，Value
   和Query/Key的维度可以不一致。
2. Key
   和Value
   的长度必须一致。Key和Value本质上对应了同一个Sequence在不同空间的表达。
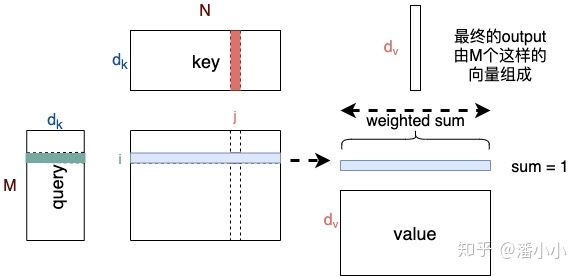
3. Attention得到的Output
   的维度和Value的维度一致，长度和Query一致。
4. Output每个位置 i 是由value的所有位置的vector加权平均之后的向量；而其权值是由位置为i 的query和key的所有位置经过attention计算得到的 ，权值的个数等于key/value的长度。

Attention示意图

在经典的Transformer结构中，我们记线性映射之前的Query, Key, Value为q, k, v，映射之后为Q, K, V。那么:

1. self-attention的q, k, v都是同一个输入, 即当前序列由上一层输出的高维表达。
2. cross-attention的q代表当前序列，k,v是同一个输入，对应的是encoder最后一层的输出结果(对decoder端的每一层来说，保持不变)

而每一层线性映射参数矩阵都是独立的，所以经过映射后的Q, K, V各不相同，模型参数优化的目标在于将q, k, v被映射到新的高维空间，使得每层的Q, K, V在不同抽象层面上捕获到q, k, v之间的关系。一般来说，底层layer捕获到的更多是lexical-level的关系，而高层layer捕获到的更多是semantic-level的关系。

2.4. Attention的作用

下面这段我会以机器翻译为例，用通俗的语言阐释一下attention的作用，以及query, key, value的含义。

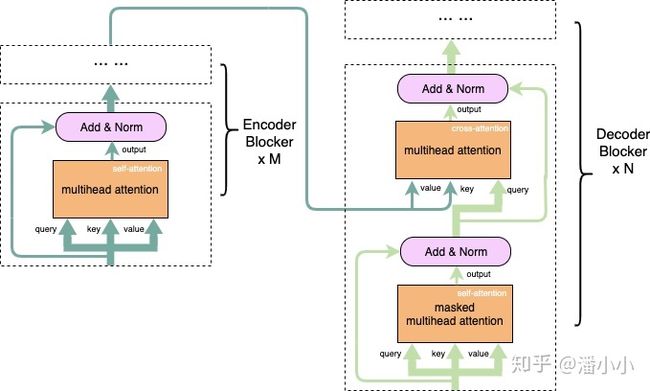
Transformer模型Encoder, Decoder的细节图（省去了FFN部分）

query对应的是需要被表达的序列(称为序列A)，key和value对应的是用来表达A的序列(称为序列B)。其中key和query是在同一高维空间中的(否则无法用来计算相似程度)，value不必在同一高维空间中，最终生成的output和value在同一高维空间中。上面这段巨绕的话用一句更绕的话来描述一下就是:

序列A和序列B在高维空间

中的高维表达

的每个位置

分别和

计算相似度，产生的权重作用于序列B在高维空间

中的高维表达

，获得序列A在高维空间

中的高维表达

Encoder部分中只存在self-attention，而Decoder部分中存在self-attention和cross-attention

【self-attention】encoder中的self-attention的query, key, value都对应了源端序列(即A和B是同一序列)，decoder中的self-attention的query, key, value都对应了目标端序列。

【cross-attention】decoder中的cross-attention的query对应了目标端序列，key, value对应了源端序列(每一层中的cross-attention用的都是encoder的最终输出)

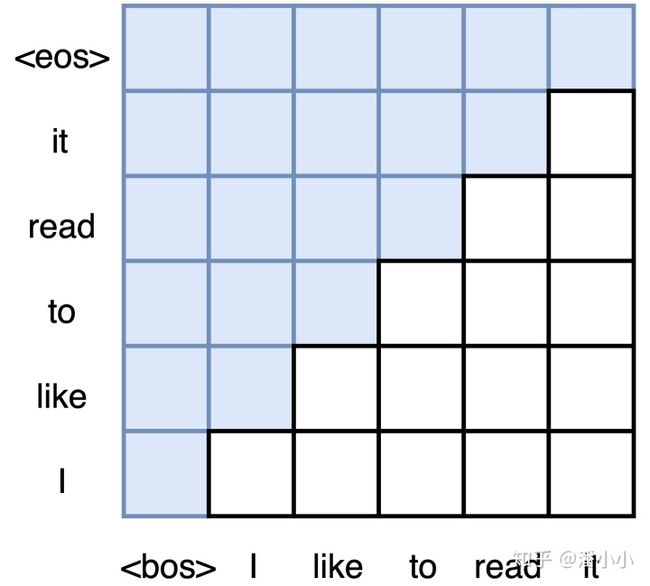
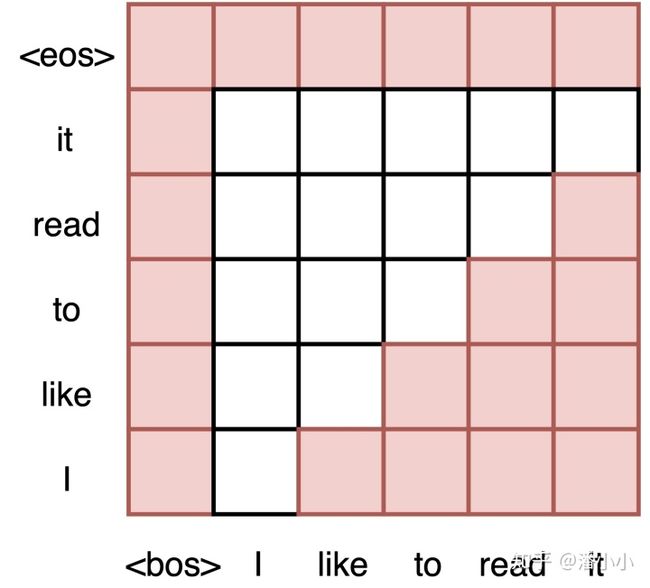
2.5. Decoder端的Mask

Transformer模型属于自回归模型（p.s. 非自回归的翻译模型我会专门写一篇文章来介绍），也就是说后面的token的推断是基于前面的token的。Decoder端的Mask的功能是为了保证训练阶段和推理阶段的一致性。

论文原文中关于这一点的段落如下：

We also modify the self-attention sub-layer in the decoder stack to prevent from attending to subsequent positions. This masking, combined with the fact that the output embeddings are offset by one position, ensures that the predictions for position i can depend only on the known outputs at positions less than i.

在推理阶段，token是按照从左往右的顺序推理的。也就是说，在推理timestep=T的token时，decoder只能“看到”timestep < T的 T-1 个Token, 不能和timestep大于它自身的token做attention（因为根本还不知道后面的token是什么）。为了保证训练时和推理时的一致性，所以，训练时要同样防止token与它之后的token去做attention。

2.6. 多头Attention (Multi-head Attention)

Attention是将query和key映射到同一高维空间中去计算相似度，而对应的multi-head attention把query和key映射到高维空间

的不同子空间

中去计算相似度。

为什么要做multi-head attention？论文原文里是这么说的:

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.

也就是说，这样可以在不改变参数量的情况下增强每一层attention的表现力。

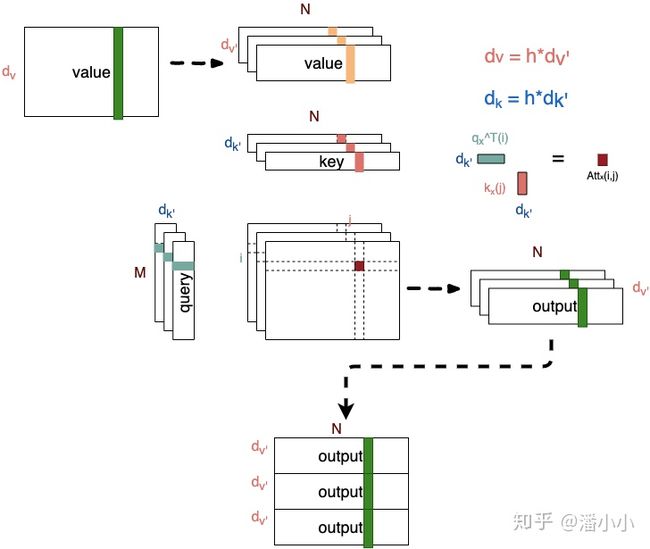
Multi-head Attention示意图

Multi-head Attention的本质是，在参数总量保持不变的情况下，将同样的query, key, value映射到原来的高维空间的不同子空间中进行attention的计算，在最后一步再合并不同子空间中的attention信息。这样降低了计算每个head的attention时每个向量的维度，在某种意义上防止了过拟合；由于Attention在不同子空间中有不同的分布，Multi-head Attention实际上是寻找了序列之间不同角度的关联关系，并在最后concat这一步骤中，将不同子空间中捕获到的关联关系再综合起来。

从上图可以看出，

和

之间的attention score从1个变成了h个，这就对应了h个子空间中它们的关联度。

3. Transformer模型架构中的其他部分

3.1. Feed Forward Network

每一层经过attention之后，还会有一个FFN，这个FFN的作用就是空间变换。FFN包含了2层linear transformation层，中间的激活函数是ReLu。

曾经我在这里有一个百思不得其解的问题：attention层的output最后会和

相乘，为什么这里又要增加一个2层的FFN网络？

其实，FFN的加入引入了非线性(ReLu激活函数)，变换了attention output的空间, 从而增加了模型的表现能力。把FFN去掉模型也是可以用的，但是效果差了很多。

3.2. Positional Encoding

位置编码层只在encoder端和decoder端的embedding之后，第一个block之前出现，它非常重要，没有这部分，Transformer模型就无法用。位置编码是Transformer框架中特有的组成部分，补充了Attention机制本身不能捕捉位置信息的缺陷。

position encoding

Positional Embedding的成分直接叠加于Embedding之上，使得每个token的位置信息和它的语义信息(embedding)充分融合，并被传递到后续所有经过复杂变换的序列表达中去。

3.2.1. 使用Positional Encoding带来的独特优势

优势1

不得不说，使用Positional Encoding作为每个token位置的唯一表示，这一思路很NB，为什么呢?

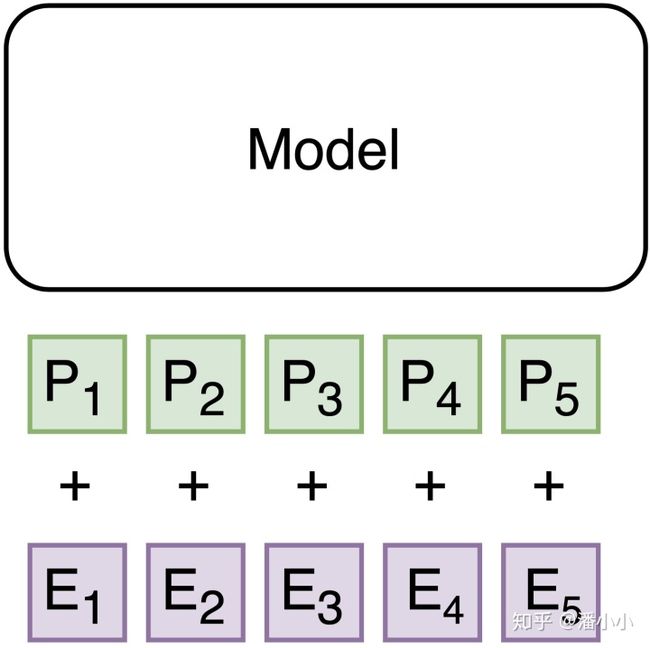
• 模型输入Encoder的每个token对应的向量有2部分:
  • Positional Encoding
  • Embedding Output
• Transformer的特性使得encoder的输入向量之间完全平等(不存在RNN那种recurrent结构)，token的实际位置和positional encoding唯一绑定，我们可以通过对positional encoding进行操作来改变token在序列中的实际位置。

[a] 输入等于Positional Encoding + Embedding Output

* 对inference阶段而言

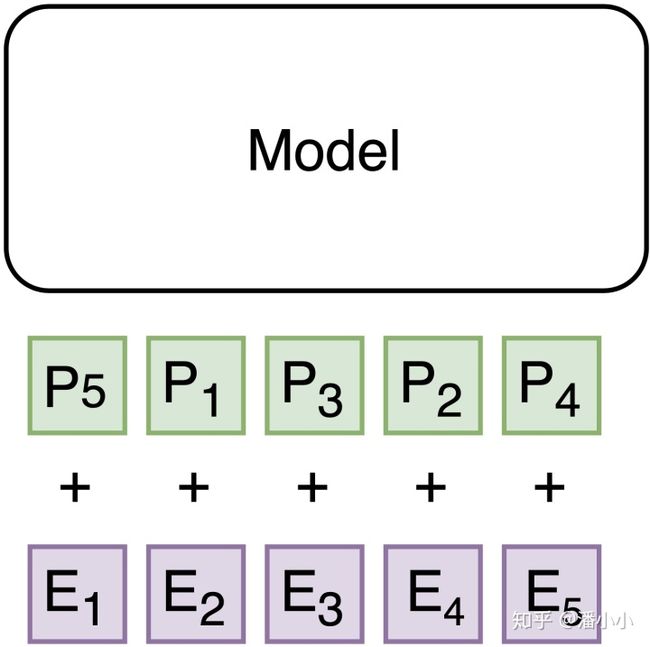
• 下图[b]中的输入Embedding部分没有变化，但是Positional Encoding部分被打乱了顺序
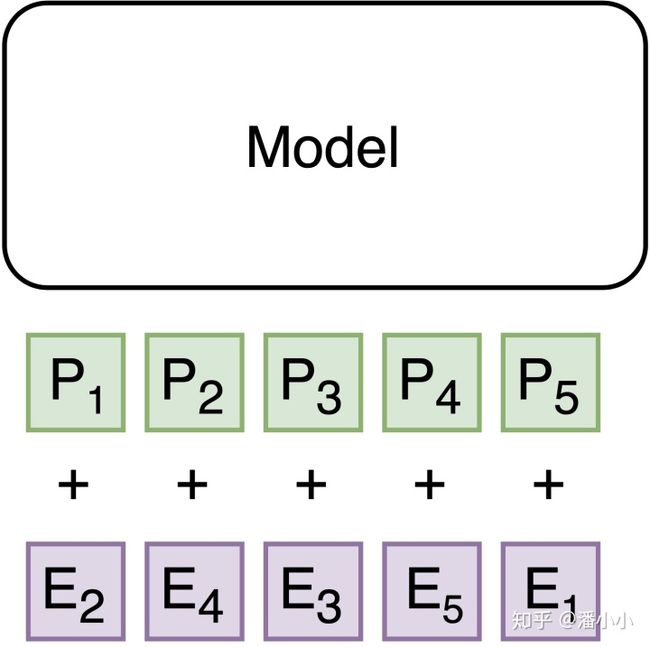
• 下图[c]中的Positional Encoding部分没有变化，但是Embedding部分被打乱了顺序
• 实际上[b]和[c]完全等价，因为在2种输入中E1-P5, E2-P1, E3-P3, E4-P2, E5-P4这个对应关系恒定。

[b] 输入token顺序不变，只改变positional encoding顺序

[c] 输入positional encoding顺序不变，token顺序改变

* 对train阶段而言(针对learned postional encoding的情况)

• 由于positional encoding是训练出来的，那么它在inference阶段代表哪个位置，完全由训练时的实际位置决定
• 举个例子，在decoder中，cross-attention模块是有mask的，目的是防止token与它之后的token去做attention，也就是left-to-right模型。如果这时我突然想要训一个right-to-left的模型，那么做法1是在预处理阶段将序列翻转过来(比较简单也比较容易想到)；做法2是在训练时将mask策略换一下

Left-to-Right模型训练时对应的decoder mask

Right-to-Left模型训练时对应的decoder mask

• 做法1和做法2训练出来的positional encoding是等价的
• 【延伸】有兴趣可以看看XLNet是如何利用mask来实现Permuted Language Model的: 潘小小：【论文串讲】从GPT和BERT到XLNet

优势2

论文中使用的Positional Encoding(PE)是正余弦函数，位置(pos)越小，波长越长，每一个位置对应的PE都是唯一的。同时作者也提到，之所以选用正余弦函数作为PE，是因为这可以使得模型学习到token之间的相对位置关系：因为对于任意的偏移量k，

可以由

的线性表示：

上面两个公式可以由

和

的线性组合得到。也就是

乘上某个线性变换矩阵就得到了

p.s. 后续有一个工作在attention中使用了“相对位置表示” (Self-Attention with Relative Position Representations) ，有兴趣可以看看。

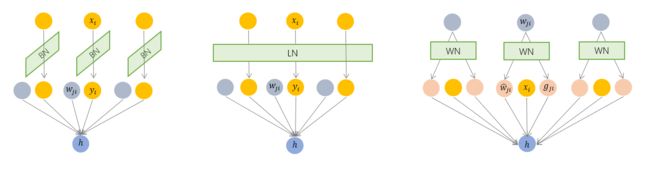
3.3. Layer Normalization

在每个block中，最后出现的是Layer Normalization。Layer Normalization是一个通用的技术，其本质是规范优化空间，加速收敛。

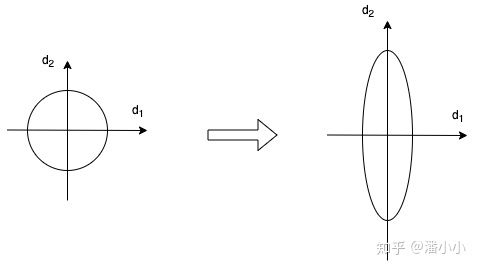
当我们使用梯度下降法做优化时，随着网络深度的增加，数据的分布会不断发生变化，假设feature只有二维，那么用示意图来表示一下就是：

数据的分布发生变化，左图比较规范，右图变得不规范

为了保证数据特征分布的稳定性（如左图），我们加入Layer Normalization，这样可以加速模型的优化速度。

4. 参考

How Much Attention Do You Need? A Granular Analysis of Neural Machine Translation Architectures​www.aclweb.org Attention is all you need; Attentional Neural Network Models | Łukasz Kaiser | Masterclass​www.youtube.com The Illustrated Transformer​jalammar.github.io

Juliuszh：详解深度学习中的Normalization，BN/LN/WN​zhuanlan.zhihu.com

其他......

本文只是重点介绍了一下Transformer，当前基于Transformer的各类后续研究正在自然语言处理的各大领域里大放异彩，本人还有一些其他的文章与Transformer有关:

潘小小：【论文串讲】从GPT和BERT到XLNet​zhuanlan.zhihu.com

潘小小：【论文串讲】从BERT和XLNet到MPNet 潘小小：【论文串讲】从GPT和BERT到XLNet​zhuanlan.zhihu.com

潘小小：【论文串讲】从BERT和XLNet到MPNet​zhuanlan.zhihu.com

---

本文已独家授权公众号浅梦的学习笔记发布在微信公众平台。

---

花絮！

终于写完啦～撒花

大家好，我叫潘小小（不是真名），是字节跳动AI-lab的一枚算法攻城狮～我的文章中绝大部分的图文都是原创，行文风格比较偏我个人学习和思考的习惯。欢迎大家关注我的技术专栏【小小的机器世界】