机器学习之线性回归(手推公式版)
文章目录
-
- 前言
- 1. 线性回归 ( L i n e a r (Linear (Linear M o d e l ) Model) Model)
-
- 1.1 一元线性回归
- 1.2 多元线性回归 ( M u l t i v a r i a t e (Multivariate (Multivariate L i n e a r Linear Linear M o d e l ) Model) Model)
- 2. 模型实现
- 3. 模型评估
- 结束语
前言
回归 ( R e g r e s s i o n ) (Regression) (Regression),用于预测输入变量(自变量)与输出变量(因变量)之间的关系,即当输入的值发生变化时,输出的值也随之变化。它属于监督学习,即需要给定一个训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\{(x_1,y_1),(x_2,y_2),\dots,(x_m,y_m)\} D={ (x1,y1),(x2,y2),…,(xm,ym)},就拿股票预测来说吧,将股票以往的历史数据作为训练集来学习一个模型,根据当前的股票信息来预测下一个时间的股票价格。学习得到的模型我们称之为回归函数 f ( x ) f(x) f(x)。
1. 线性回归 ( L i n e a r (Linear (Linear M o d e l ) Model) Model)
线性回归的基本形式:给定有 d d d个属性描述的示例 x = [ x 1 x 2 ⋮ x d ] \bm {x}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots\\ x_d\\ \end{bmatrix} x=⎣⎢⎢⎢⎡x1x2⋮xd⎦⎥⎥⎥⎤,其中 x i x_i xi是 x \bm {x} x在第 i i i个属性上的取值,线性模型试图学得一个由属性 x i x_i xi线性组合的预测函数,即 f ( x ) = w 1 x 1 + w 2 x 2 + ⋯ + w d x d + b f(\bm {x})=w_1x_1+w_2x_2+\dots+w_dx_d+b f(x)=w1x1+w2x2+⋯+wdxd+b
一般用向量形式表示为 f ( x ) = w T x + b f(\bm {x})=\bm {w^Tx}+b f(x)=wTx+b
其中 w = [ w 1 w 2 ⋮ w d ] \bm {w}=\begin{bmatrix} w_1 \\ w_2 \\ \vdots\\ w_d\\ \end{bmatrix} w=⎣⎢⎢⎢⎡w1w2⋮wd⎦⎥⎥⎥⎤,参数 w \bm {w} w和 b b b是通过学习得到的,这两个参数确定即代表模型就确定了。
1.1 一元线性回归
这应该是最基本的线性回归了,即输入的变量只有一个。对于给定的数据集 D = { ( x i , y i ) } D=\{(x_i,y_i)\} D={ (xi,yi)},其中 1 ≤ i ≤ m 1 \leq i \leq m 1≤i≤m,一元线性回归试图学得
f ( x i ) = w x i + b , 使 得 f ( x i ) 无 限 接 近 于 y i f(x_i)=wx_i+b,使得f(x_i)无限接近于y_i f(xi)=wxi+b,使得f(xi)无限接近于yi
确定参数 w w w和 b b b,关键在于如何衡量 f ( x ) f(x) f(x)与 y y y之间的差别,均方误差 ( M e a n (Mean (Mean S q u a r e Square Square E r r o r , M S E ) Error,MSE) Error,MSE)是回归任务中最常用的性能度量,试图让均方误差最小化来求得最优的 w w w和 b b b,即 ( w ∗ , b ∗ ) = a r g m i n ∑ i = 1 m ( f ( x i ) − y i ) 2 = a r g m i n ∑ i = 1 m ( y i − w x i − b ) 2 (w^*,b^*)=argmin\sum_{i=1}^m(f(x_i)-y_i)^2 \\ =argmin\sum_{i=1}^m(y_i-wx_i-b)^2 (w∗,b∗)=argmini=1∑m(f(xi)−yi)2=argmini=1∑m(yi−wxi−b)2
知识小提示:均方误差也称为
平均损失( S q u a r e (Square (Square L o s s ) Loss) Loss)
如何求解呢?对于上述公式来数,我们可以再次简化成 y = x 2 y=x^2 y=x2,求解使 y y y取最小值时的 x x x,很好办,上来就是求导,令倒数等于0,没错,就是这样。我们这里求解的是两个未知数,所以求的是偏导数,求解如下:
知识小提示:凸函数,即二阶导数在区间上非负,若恒大于0,称为严格凸函数,这和高数里面的定义正好相反。西瓜书上具体定义如下:
假设函数 f ( x ) f(x) f(x)的定义域为 [ a , b ] [a,b] [a,b],在其区间上任取两点,若 f ( x 1 ) + f ( x 2 ) 2 \frac {f(x_1)+f(x_2)} {2} 2f(x1)+f(x2) ≥ \geq ≥ f ( x 1 + x 2 2 ) {f(\frac {x_1+x_2} {2})} f(2x1+x2),则称 f ( x ) f(x) f(x)为凸函数。
1.2 多元线性回归 ( M u l t i v a r i a t e (Multivariate (Multivariate L i n e a r Linear Linear M o d e l ) Model) Model)
即输入的变量有多个,正如最上面的基本形式。多元线性回归试图学得
f ( x i ) = w T x i + b , 使 得 f ( x i ) 无 限 接 近 于 y i f(\bm {x_i})=\bm {w^Tx_i}+b,使得f(\bm {x_i})无限接近于y_i f(xi)=wTxi+b,使得f(xi)无限接近于yi
同样,可以利用最小二乘法进行上述求解,为了方便,这里把 w \bm {w} w和 b b b吸收入向量形式 w ^ = [ w b ] \bm {\hat {w}}=\begin{bmatrix} \bm {w} \\ b \\ \end{bmatrix} w^=[wb],则 w ^ ∗ = a r g m i n ∑ i = 1 m ( f ( x i ) − y i ) 2 = a r g m i n ∑ i = 1 m ∣ ∣ y − X w ^ ∣ ∣ 2 2 = a r g m i n ∑ i = 1 m ( y − X w ^ ) T ( y − X w ^ ) \bm {\hat {w}^*}=argmin\sum_{i=1}^m(f(\bm {x_i})-\bm {y_i})^2 \\ =argmin\sum_{i=1}^m||\bm {y}-\bm {X\hat {w}}||_2^2 \\ =argmin\sum_{i=1}^m(\bm {y}-\bm {X\hat {w}})^T(\bm {y}-\bm {X\hat {w}}) w^∗=argmini=1∑m(f(xi)−yi)2=argmini=1∑m∣∣y−Xw^∣∣22=argmini=1∑m(y−Xw^)T(y−Xw^) 具体求解如下:
知识小提示:基于均方误差最小化进行求解的方法称为
最小二乘法。在统计学中,使用最小二乘法来求解线性回归的方法是一种无偏估计的方法,这种无偏估计要求因变量(即标签 y y y)必须服从正态分布,所以当线性回归模型效果不好时,考虑正态化处理来改变一下因变量的分布。
2. 模型实现
这里使用sklearn.linear_model里的LinearRegression进行线性回归建模,数据集为sklearn自带的糖尿病数据集diabetes,数据集详情大致如下:

| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 |
|---|---|---|---|---|---|---|---|---|---|
| 年龄 | 性别 | 体重指数 | 平均血压 | T细胞数 ( t c ) (tc) (tc) | 低密度脂蛋白 ( l d l ) (ldl) (ldl) | 高密度脂蛋白 ( h d l ) (hdl) (hdl) | 促甲状腺激素 ( t c h ) (tch) (tch) | l a m o t r i g i n e ( l t g ) lamotrigine(ltg) lamotrigine(ltg) | 血糖含量 ( g l u ) (glu) (glu) |
详情可打印
diabetes.DESCR
from sklearn import linear_model
from sklearn import model_selection
from sklearn import datasets
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
import pandas as pd
import matplotlib.pyplot as plt
# 加载糖尿病数据集
diabetes = datasets.load_diabetes()
# print(diabetes.DESCR)
# data = pd.DataFrame(diabetes.data)
# data.columns = diabetes.feature_names
# data['target'] = diabetes.target
data = diabetes.data
target = diabetes.target
# 划分训练集和测试集
x_train, x_test, y_train, y_test = model_selection.train_test_split(data, target, test_size=0.3, random_state=512)
# 创建线性回归模型
model= linear_model.LinearRegression()
# 训练这个模型
model.fit(x_train, y_train)
# score = model.score(x_test, y_test)
# 使用模型做预测
y_pred = model.predict(x_test)
# 查看各个特征的系数
w = model.coef_
b = model.intercept_
print('w: {0}\nb: {1}'.format(w, b))
各个特征对应的系数如下:

由上可以看出,s5与糖尿病有很大的关联,其次是s2,而s1和性别与糖尿病的关联很小(额(⊙o⊙)…这样分析总感觉有点…)。
有关
LinearRegression的详细参数说明可参考官方手册
3. 模型评估
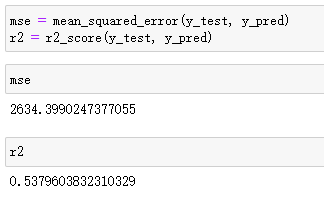
在线性回归的模型评估中常用两种方法,一种就是上面所述的均方误差 M S E MSE MSE,另一种就是 R R R方值 R 2 _ s c o r e R2\_score R2_score。 M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 MSE=\frac {1} {m} \sum_{i=1}^m(y_i-\hat {y}_i)^2 MSE=m1i=1∑m(yi−y^i)2 可见, M S E MSE MSE衡量的是模型对样本数值的拟合能力, M S E MSE MSE越小,表示模型对数据拟合的越好,但它有可能对部分数值拟合的很好,而对数据的分布可能拟合的不好,尤其是在数据上下界限附近。 R 2 _ s c o r e = 1 − ∑ i = 1 m ( y i − y ^ i ) 2 ∑ i = 1 m ( y i − y ‾ ) 2 R2\_score=1-\frac {\sum_{i=1}^m(y_i-\hat {y}_i)^2} {\sum_{i=1}^m(y_i-\overline {y})^2} R2_score=1−∑i=1m(yi−y)2∑i=1m(yi−y^i)2 分式上的分子表示真实值和预测值之间的差值,也就是模型没有捕捉到的,分母是真实标签所带的信息量,可见, R 2 _ s c o r e R2\_score R2_score衡量的是模型对捕获到的信息量占真实标签中所带的信息量的比例。 R 2 _ s c o r e R2\_score R2_score越接近于1,表示模型对数据拟合的越好。
方差可以用来衡量数据上的信息量,如果方差越大,代表数据上的信息量越多,这些信息量不仅包括数值的大小,还包括数据中隐藏的规律,比如,数据的分布规律。
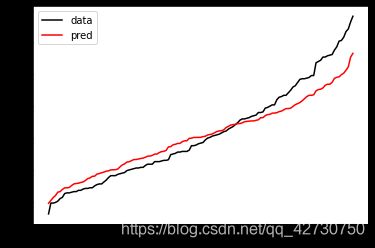
# 绘制输出
plt.plot(range(len(y_test)), sorted(y_test), color='black', label='data')
plt.plot(range(len(y_pred)), sorted(y_pred), color='red', label='pred')
plt.legend()
plt.show()
结束语
持续充电中,博客内容也在不断更新补充中,如有错误,欢迎来私戳小编哦!共同进步,感谢Thanks♪(・ω・)ノ