李宏毅机器学习2020春季作业一hw1

作业介绍

题目要求：利用每天的前9个小时的18个特征（包括PM2.5），来预测第10个小时的PM2.5的值。

特征包括为： AMB_TEMP, CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL, RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR，总计18种。、

tset.csv、train.csv、相关作业更详细的介绍视频、图片等已上传

资料下载方式请戳链接（免费）https://download.csdn.net/download/qq_46126258/14157237
也可以从网站上直接下载（需要外网VPN，因为是台湾链接地址）
https://drive.google.com/open?id=1El0zvTkrSuqCTDcMpijXpADvJzZC2Jpa

train.csv 的资料为 12 个月中，每个月取 20 天，每天 24 小时(0-23)的资料(每个小时有 18 个 features)

作业介绍的视频可以参考B站视频：bilibili.com/video/BV1LE411T7ns?from=search&seid=11523587886734781073
或者直接解压免费的资料

步骤分析：

注：所有代码是在jupyter notebook上运行的

1、Load ‘train.csv’

导入需要的包

import sys
import pandas as pd
import numpy as np
data = pd.read_csv('hw1-regression-20210111T040736Z-001\hw1-regression/train.csv', encoding = 'big5')

train.csv内的数据如下：

2、Preprocessing

处理数据：
思路：用WPS打开train.csv查看数据的格式：

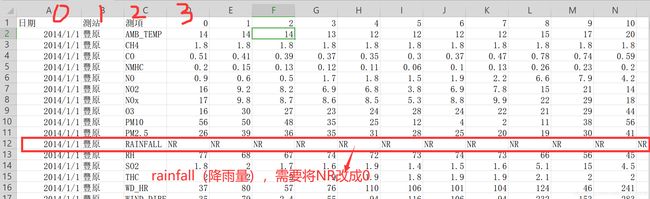
发现有一栏特征叫RAINFALL，有降雨量的时候写了数据，没有降雨的时候写的NR（Not Rain），所以我们做处理的时候要 data[data == 'NR'] = 0，并且取所有行的第3列到最后1列的数据
代码实现：

data = data.iloc[:, 3:]
data[data == 'NR'] = 0
raw_data = data.to_numpy()#将DataFrame转换为NumPy数组,才能进行相应运算

3、Extract Features (1)

思路：查看train.csv的我们观察到：去掉第一行表头，在表中共有12个月中前20天的数据。每天24小时记录18行的feature（那么每天可以由18╳24的矩阵表示），所以我们进行下图的操作，以便后续操作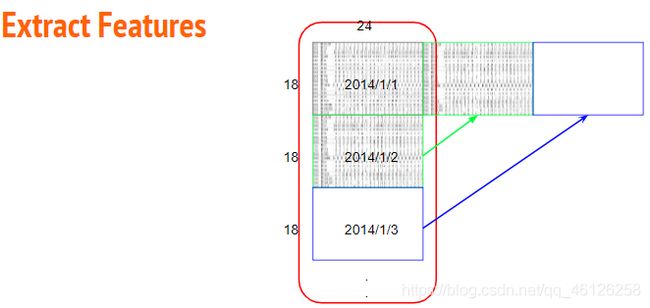
即将一个月抽取的20天里代表每天的矩阵放在一行，方便后续处理。每个月有20天，每天有24小时，一个月480个小时，所以一个月由18╳480的矩阵表示，12个月由18行╳12*480列的矩阵表示
range(12)是从0开始，11结束；range(20)是从0开始，19结束
步骤：
（1）先从raw_data中取表示一天的矩阵：raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
例：在raw_data中找2.2日的数据，每天有18行，2.2日前有21天即起始点18 * (20 * 1 + 1)， 中间间隔18行，结束点18 * (20 * 1 +1 + 1)
（2）将取好的矩阵赋值给month_data：
首先找month_data的对应位置，month_data中是20天一赋值，例：找到2.2日的位置（长24宽18）每天占24列，2.2日前有21天（20天为前一个月）即起始点1 * 24，间隔24列，终止点(1 + 1) * 24）
（3）同（2）取好每天的矩阵，再将20天的数据整合在一个月month_data中：
sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]

month_data = {
     }##按照month做索引，方便以后的数据查找
for month in range(12):##求12个每月
    sample = np.empty([18, 480])##初始化每月：18X480
    for day in range(20):##每个月的20天
        sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
    month_data[month] = sample##将求好的单月赋值

具体的矩阵移位建议在纸上演算一遍

3、Extract Features (2)

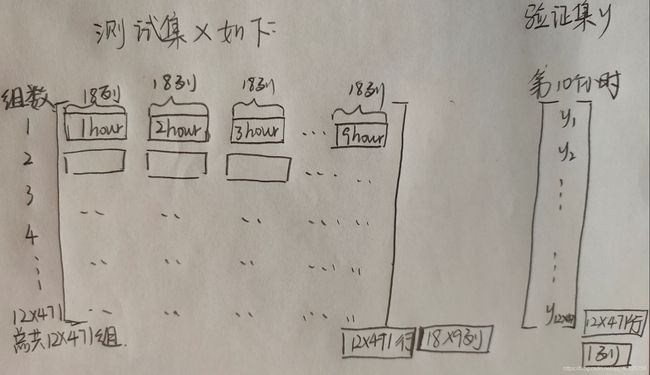
根据题意，为训练集分组，前9个小时做训练集，第10个小时做验证集，所以将10个小时划为一组数据。现在我们每个月有480个小时，共12个月。分组方式为每间隔一个小时取一组。
思路：按照上述方法每个月会得到 471 组数据（最后一组需要时长9小时），一年12个月会有 471 * 12 = 5652 组数据（即 472 * 12 个测试集x，每个测试集有 9 * 18的 features ；对应472 * 12 个验证集y：PM2.5的值）直观的方式见下图

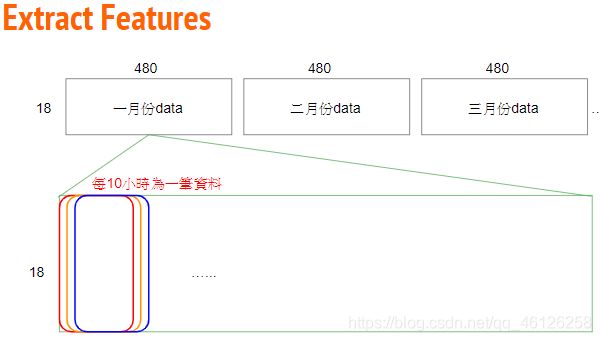
处理好的结果见下：

实现代码如下：
这里说明一下$.reshape(1,-1)：$
我希望赋值的时候是一行一行的即每次1行x列（x表示未知），如果不想手算x，可以用.reshape(1, -1)解决这个问题。也可以手算后用.reshape(1,18)
Numpy允许给新排布的参数设置为 -1，它指的是未知的维数，前提是已知另一维度（如(2, -1), (-1, 3)，但是不允许(-1, -1)），Numpy自己会根据输入值的排布，用reshape()方法得出未知维数的值，使得输出值符合np.reshape()的规范。详细说明见另一博主链接

x = np.empty([12 * 471, 18 * 9], dtype = float)
y = np.empty([12 * 471, 1], dtype = float)
'''
注释掉的这部分为老师的做法
for month in range(12):##12个月
    for day in range(20):##每个月20天
        for hour in range(24):##每天24小时（0-23）
            if day == 19 and hour > 14:
                continue
            x[month * 471 + day * 24 + hour, :] = month_data[month][:,day * 24 + hour : day * 24 + hour + 9].reshape(1, -1) 
            #vector dim:18*9 (9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9)
            y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9] #value
            '''
#由于已经将一个月的数据合并，那么天与小时都已经是次要的信息。
#因此，此处对于1个月，只需要一个index，从0到471取到就可以了            
for month in range(12):
    for index in range(471):
        x[index + 471 * month, :] = month_data[month][:, index:index + 9].reshape(1, -1)
        y[index + 471 * month, :] = month_data[month][9, index + 9]
print(x)
print(y)
'''
[[14.  14.  14.  ...  2.   2.   0.5]
 [14.  14.  13.  ...  2.   0.5  0.3]
 [14.  13.  12.  ...  0.5  0.3  0.8]
 ...
 [17.  18.  19.  ...  1.1  1.4  1.3]
 [18.  19.  18.  ...  1.4  1.3  1.6]
 [19.  18.  17.  ...  1.3  1.6  1.8]]
[[30.]
 [41.]
 [44.]
 ...
 [17.]
 [24.]
 [29.]]
 '''

4、Normalize (1)

数据标准化之后模型更容易收敛，也更快收敛，方法就是让其减去均值再除以标准差。

mean()函数功能：求取均值. np.std（标准差）同理
经常操作的参数为axis，以m × n矩阵举例：
axis 不设置值，对 m × n 个数求均值，返回一个实数
axis = 0：压缩行，对各列求均值，返回 1 × n 矩阵
axis =1 ：压缩列，对各行求均值，返回 m × 1 矩阵

mean_x = np.mean(x, axis = 0) #18 * 9 列均值
std_x = np.std(x, axis = 0) #18 * 9 # 列标准差
for i in range(len(x)): #12 * 471
    for j in range(len(x[0])): #18 * 9 
        if std_x[j] != 0:
        # 每个元素减去其所在列的均值，再除以标准差
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
x
'''
array([[-1.35825331, -1.35883937, -1.359222  , ...,  0.26650729,
         0.2656797 , -1.14082131],
       [-1.35825331, -1.35883937, -1.51819928, ...,  0.26650729,
        -1.13963133, -1.32832904],
       [-1.35825331, -1.51789368, -1.67717656, ..., -1.13923451,
        -1.32700613, -0.85955971],
       ...,
       [-0.88092053, -0.72262212, -0.56433559, ..., -0.57693779,
        -0.29644471, -0.39079039],
       [-0.7218096 , -0.56356781, -0.72331287, ..., -0.29578943,
        -0.39013211, -0.1095288 ],
       [-0.56269867, -0.72262212, -0.88229015, ..., -0.38950555,
        -0.10906991,  0.07797893]])
'''

5、Training

模型：线性函数
输入：一次18×9个数据
参数：18×9个权重+一个偏置
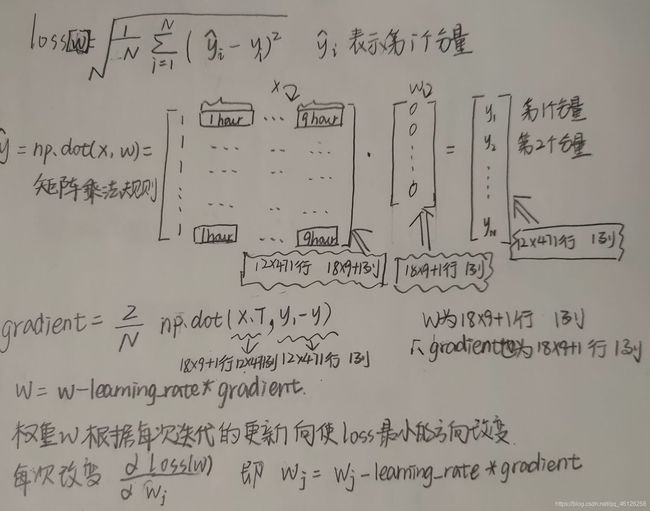
损失函数：均方根误差（见下图）
优化算法：gradient（梯度下降）、Adagrad
np.concatenate((a,b),axis=1) ： 进行行拼接，拼接结果是[a,b]，相当于在x矩阵的左侧第一列添加同等行数的1。
np.dot(a,b)：a与b进行矩阵乘法
详细的numpy——np.array、np.matrix、np.mat的区别及（*）、np.multiply、np.dot乘法的区别，请戳链接
np.power(a,b)：a的b次方根
x.T等价于x.transpose()：求矩阵x的转置

（1）梯度下降法（BGD）优化

代码实现如下：

dim = 18 * 9 + 1 # w的行数，w为18*9+1行：1列
w = np.ones([dim, 1]) 
#不要写成w = np.zeros([dim, 1])，否则会梯度爆炸或消失使loss值为nan
x = np.concatenate( (np.ones([12 * 471, 1]), x), axis=1).astype(float)
N = 12 * 471 # x的行数，也是计算得出的y冒的行数

learning_rate = 0.03
iter_time = 1000
loss = np.zeros([iter_time, 1]) # 每次迭代loss更新，所以与迭代次数相同
for i in range(iter_time):
    y1 = np.dot(x, w) #w和x的顺序不能反(5652, 163)*(163, 1)=(5652, 1)
    loss[i] = np.sqrt(np.sum(np.power(y1-y, 2)) / N)
    gradient = (2/N) * np.dot(x.T, y1-y)
    w = w - learning_rate * gradient

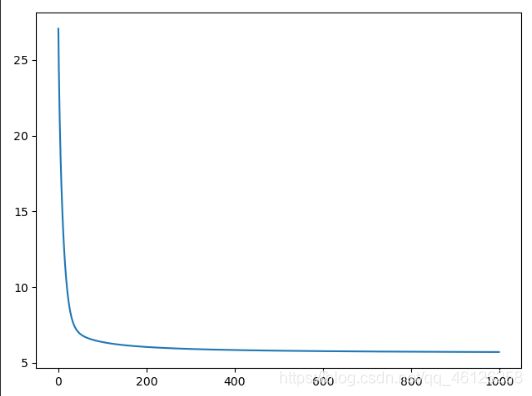
plt.plot(loss)
plt.show()

从左到右依次是0.01，0.03，0.05和的学习率，迭代了1000次，较高的学习率无法收敛，较低的学习率收敛慢

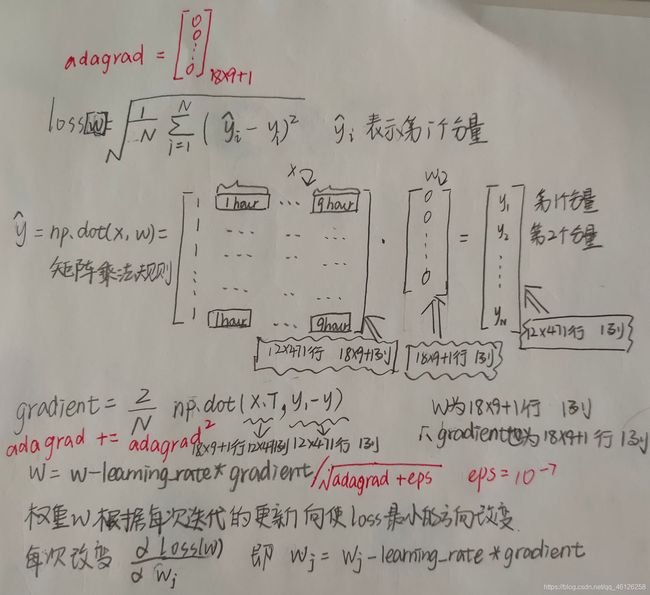
（2）AdaGrad优化

在上一个算法中的learning_rate是凭借试验和经验设置的，那么可不可以让他自己根据每一步求出的$w^t$自己更新，自动地调节学习率呢？答案是有的——AdaGrad算法：一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢

在这里我们单独考虑每一个$w^t$，对于不同的$w^t$会有不同的学习效率，首先提出两个公式：
其中${\eta }^t$为学习率，$g^t$为gradient，表示参数的偏微分。

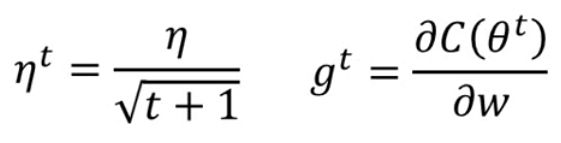
这里是BGD和Adagrad在更新参数$w^t$时的对比：

其中${\sigma }^t$是之前所有$w^t$的标准差（平方和开根号），也就是下图这样

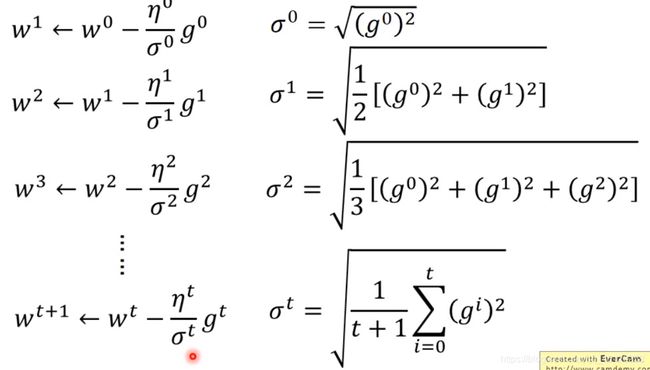
然后我们发现最终$w^t$更新的式子可以化简为这样

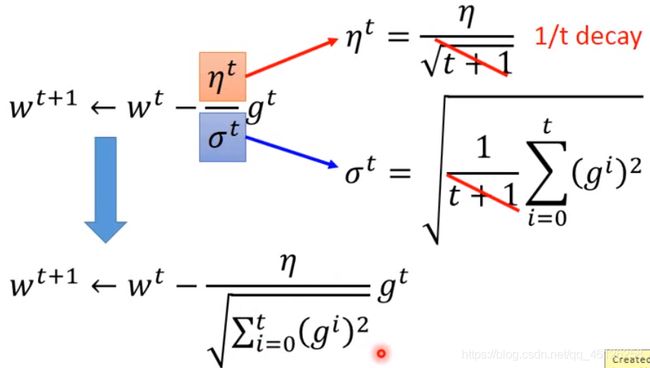
比起BGD，这种优化方法，在更新参数时，除了乘学习率外，还除了过往所有梯度平方和的平方根，可动态的改变学习率。并且不会因为某时梯度太大而导致模型发散

下图的红色部分为二者的区别

dim = 18 * 9 + 1 # w的行数，w为18*9+1行：1列
w = np.ones([dim, 1]) 
x = np.concatenate((np.ones([12 * 471, 1]), x), axis = 1).astype(float)
learning_rate = 100 
iter_time = 1000
adagrad = np.zeros([dim, 1])
eps = 0.0000000001# 小常数，为了数值稳定通常设置在10的-9次方
for t in range(iter_time):
    loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y,2)) / 471 / 12) #w和x的顺序不能反(5652, 163)*(163, 1)=(5652, 1)
    if(t%100==0):
        print(str(t) + ":" + str(loss))
    gradient = 2 * np.dot(x.transpose(), np.dot(x,w) - y)
    adagrad += gradient ** 2 #求adagrad的平方power(adagrad,2)
    w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
np.save('weight.npy',w)

随着迭代次数的增加，我们可以得到逐渐减小的loss

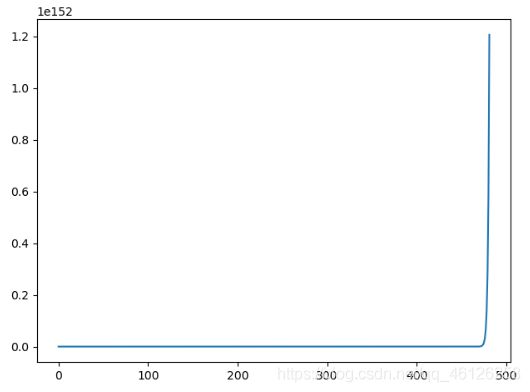
在初始化w时使用w = np.zeros([dim, 1]) 会得到下图loss下降的结果，速度没有w = np.ones([dim, 1])下降的快

6、PreTesting

将训练集按8：2比例分为组内训练集与测试集，手动测试模型训练效果，也就是拿出20%做测试集按照之前w求出对应的ans_y，通过与真实的y_validation求取loss

import math
x_train_set = x[: math.floor(len(x) * 0.8), :]#约为4521
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8): , :]#约为1131
y_validation = y[math.floor(len(y) * 0.8): , :]

w = np.load('weight.npy') #提取训练好的参数w
x_validation = np.concatenate((np.ones([1131, 1]), x_validation), axis=1).astype(float)
ans_y = np.dot(x_validation, w)
loss = np.sqrt(np.sum(np.power(ans_y - y_validation, 2)) / 1131)
print(loss) #输出误差

得到

5.486249843833246

但这些数据终归还是在自己手里已知答案的数据，还不知道对于新加入的数据的真实拟合效果，所以我们打开test.csv，对准确度进行下一步估算

7、Testing

打开test.csv，观察到一共有240天（0-239）的数据，开始分离测试集（test_x,test_y），但是发现没有关键的第10列（正常应该是前9列作为test_x，第10列作为test_y），也就是说没有给出test_y，那么接下来做出的预测结果是没办法计算准确率的，根据视频描述可以通过上传kaggle检验预测的准确率（但是本人暂时不会操作这个，所以接下来的预测结果没办法保证准确率）

接下来开始提取test_x，提取出的格式应该和做训练时的x保持一样的格式：将一天中每个小时的18列数据横摆放（下图是之前的格式）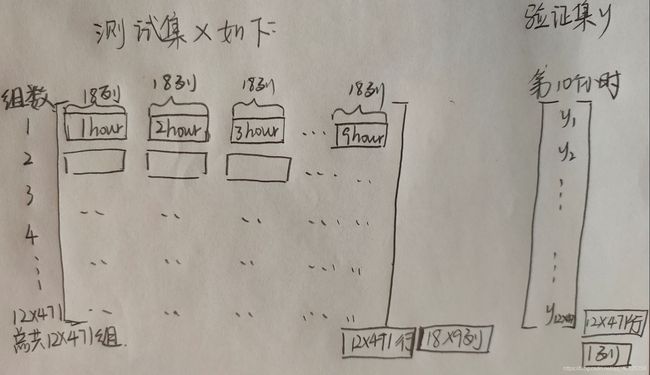
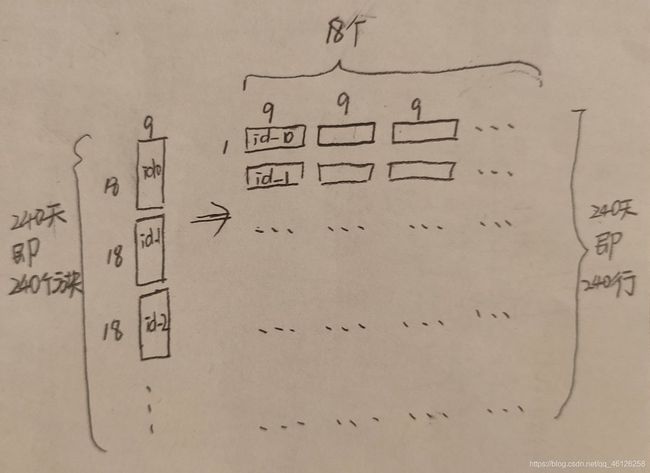
同理我们也将test_x每天的18项数据横排摆放，那么每天就有18×9列，就会得到有240行，18×9列的横排摆放的长条小方块（如下图）

代码如下：

test_data = pd.read_csv('hw1-regression-20210111T040736Z-001\hw1-regression/test.csv', header = None, encoding = 'big5')
test_data = test_data.iloc[:, 2:]
test_data[test_data == 'NR'] = 0
test_data = test_data.to_numpy()
test_x = np.empty([240, 18*9],dtype=float)
for i in range(240):#将每天的18项数据横排摆放
    test_x[i, :] = test_data[18 * i:18 * (i + 1), :].reshape(1,-1)

之前的代码已经定义：
mean_x = np.mean(x, axis = 0) 列均值
std_x = np.std(x, axis = 0) 列标准差

同样我们根据mean_x、std_x 对其进行标准化：

   for i in range(len(test_x)):#遍历每行
    for j in range(len(test_x[0])):#遍历每列
        if std_x[j]!=0:#确保分母不为0
            test_x[i][j] = (test_x[i][j] - mean_x[j])/std_x[j]

test_x = np.concatenate((np.ones([240, 1]), test_x), axis = 1).astype(float)

7、Prediction（上交作业）

算出ans_y

w = np.load('weight.npy')
ans_y = np.dot(test_x, w)
ans_y

得下图

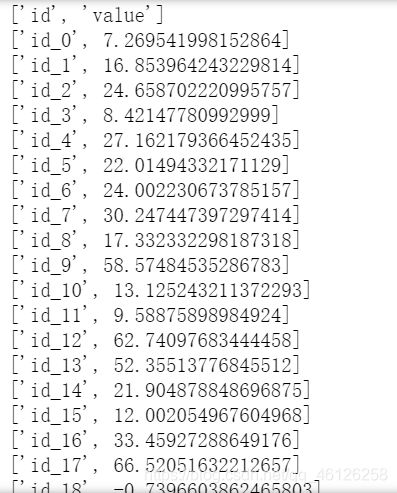
8、Save Prediction to CSV File

规范自己得出的结果，得到下图

import csv
with open('submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ['id_' + str(i), ans_y[i][0]]
        csv_writer.writerow(row)
        print(row)

有条件的小伙伴可以上传kaggle检验预测的准确率