计算几何入门 1.1:凸包的概念
一、什么是计算几何:
计算几何学(computational geometry)发展于二十世纪七十年代末,是一个正在飞速发展的新型学科。作为一个计算机算法类学科的分支,计算几何讨论更多的是计算而非几何,几何只是它的表现形式,核心还是算法。现代意义上的计算几何起源于1978年M.I.Shamos的博士论文,是计算机图形学、CAD、人工智能等多领域理论基础。计算几何可以简单理解为“算法设计与分析”课程的一个分支,是一个融入离散几何、组合几何,用几何的思想来解决问题的学科。
二、预备知识:
- 语言:C/C++
- 数据结构与算法:大O表示法,简单的复杂度分析方法,基础排序、查找等算法
- 数学:基本的高等数学、线性代数、概率论知识,离散数学基础
三、基本概念:凸包
计算几何领域几乎所有的问题都可以“归约”为凸包问题,因此学习凸包问题对整个计算几何体系至关重要。
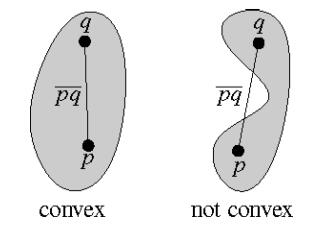
凸包(Convex Hull)定义为:
平面的一个子集S被称为是“凸”的,当且仅当对于任意两点p,s∈S,线段ps都完全属于S。(平面凸包定义)
如下图所示:
上图左边集合中任意两点组成的线段都属于该集合,因此是一个凸集,而右边集合则不是。
集合S的凸包CH(S),就是包含S的最小凸集——即包含S的所有凸集的交。
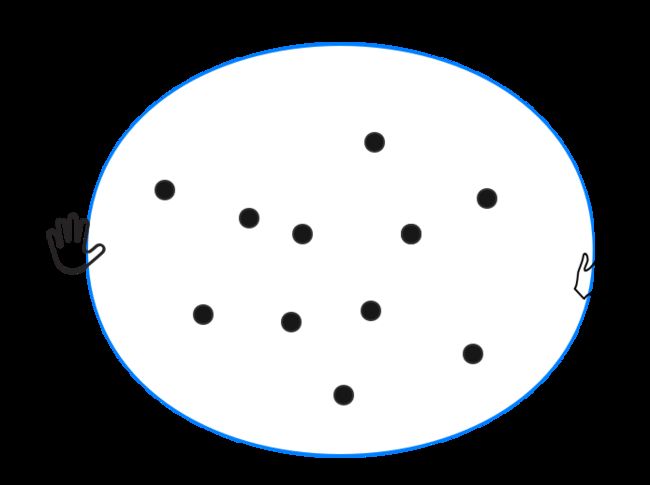
举个形象的例子来直观理解凸包。假设一个板子上有许多钉子,你撑开一个橡皮筋要去套住它们:
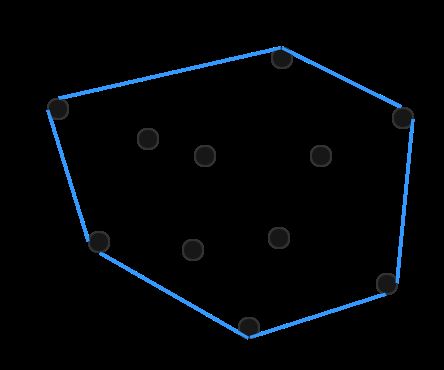
当你松手的时候橡皮筋就会变成这种状态:
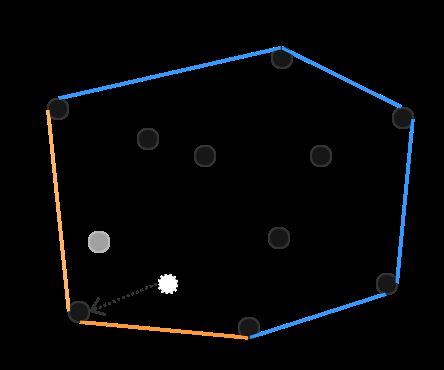
橡皮筋的状态就可以看作所谓的“凸包”。它的范围是由“外部”的一些钉子来决定的,而“内部”的钉子并不起作用。当然内部与外部都是相对而言的,若某个钉子能移动位置,就可能使某些点“起作用”,也可能使某些点失去“作用”:
1、凸包应用举例
画家绘画时经常会将几种颜料按比例混合,以得到想要的某种颜色。而所有颜色都能由红、绿、蓝三种基色混合得到(实际上是色光三原色而非美术),简化起见我们只考虑红色(R)和绿色(G)两种颜色,每种颜色可以看成红色和绿色的函数:C = (R, G)。
例如某种颜色可以表示为 X = (10%, 35%),另一种颜色为 Y = (16%, 20%)。假设我们需要的颜色为U = (12%, 30%),怎样的X和Y的比例能“勾兑”得到U呢?
答案是:两份的X加上一份的Y即可得到U,即 X:Y = 2:1。
试探性的凑出一个比值显然有些麻烦,更大的问题在于很多时候答案是凑不出来的。例如 V = (13%, 22%),无论如何是无法通过X和Y的混合得到的。此时我们可以加入另一种颜色Z = (7%, 15%),这三种颜色能否勾兑出U呢?答案是 X:Y:Z = 1:3:1。
现在的问题就能归结为:
- 给定某些颜色X, Y, Z...能否通过他们勾兑出特定颜色U
- 若能勾兑,如何计算原料比例
这就能用凸包来解决了。
凸包是一种几何模型,而几何最基础的概念就是空间,我们将颜色的欧氏空间定义为一种“颜色空间”。我们将每一种颜色都对应到颜色空间的一个点。
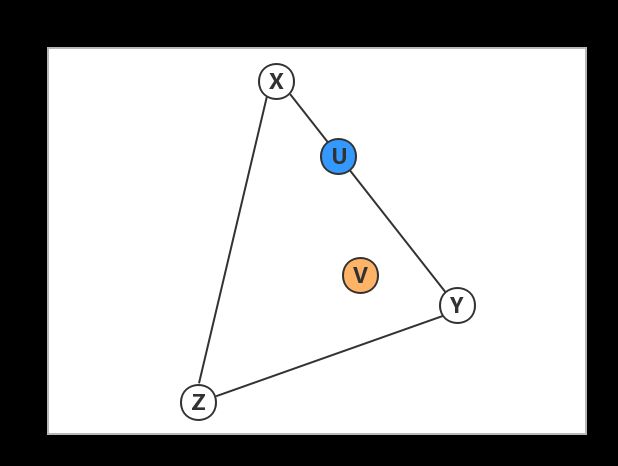
上述颜色X,Y,Z、U和V用点表示为:
X = (10, 35), Y = (16, 20), Z = (7, 15) U = (12, 30), V = (13, 22)
横轴表示红色分量数值,纵轴表示绿色分量数值,将这些点在图像上表示为:
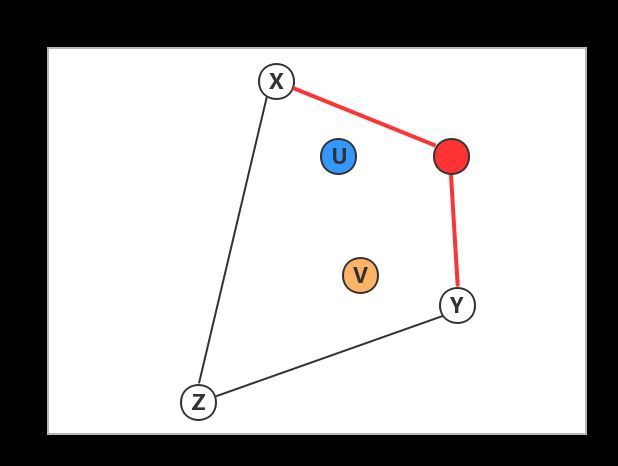
观察U和V的位置,我们发现:
U在线段XY上,并且 XU:UY = 1:2,是勾兑比例的反比,并且U的勾兑不需要X和Y之外的颜色参与(可以考虑极端情况,U在线段XY的端点上,只需要一种颜色即可);
而V并不在线段XY上,但是在X, Y, Z缩圈定的范围内,所以V能被这三种颜色勾兑出来,而V到三个原料点距离的反比正好也是勾兑比例1:3:1;
2、凸包的数学推导
上述发现有着更严格的推导证明其正确性,推导的理论基础正是凸包:
对于二维空间中点集 S = {p1, p2, ... , pn},p能被其他点的线性组合表示出来:
p = [p1, p2, ... , pn]λ = λ1p1 + λ2p2 + ... + λnpn
其中λ为一个矢量,由n个分量组成,即各点的系数(相当于勾兑比例)。其中有些组合(相当于勾兑方案)被称为凸组合(convex combination),具体来讲就是λ要满足:
λ1 + λ2 + ... + λn = 1,并且min{λ1, λ2, ... ,λn} ≥ 0
即各点系数非负(相当于所用颜料量不可能是负的)且总和为1。
如果我们新加入的颜色Z落在线段XY上,显然Z本身就能通过X和Y来勾兑,新加入Z对于勾兑出V是毫无帮助的。这种关系被称为:凸相关。当Z与X, Y不是凸相关的时候就会组成上图所示的三角形平面区域,区域内的所有颜色都能被X, Y和Z勾兑出来。若继续加入一个新的点,并且这个点与X, Y, Z凸无关,就能改变这个区域:
这和一开始我们加入新的钉子本质是一样的,点相当于钉子,而橡皮筋圈定的范围就是凸包。
本文是学堂在线课程《计算几何》的笔记,参考资料:《计算几何——算法与应用》Mark de Berg等著,邓俊辉译;《计算几何——算法设计与分析》 周培德著