排序算法
排序算法
- 1 什么是排序以及排序算法的分类
-
- 1.1 排序的概念
- 1.1 排序的分类
- 2 都有哪些排序算法
-
- 2.1 插入排序
-
- 2.1.1 直接插入排序
- 2.1.2 希尔排序
- 2.2 选择排序
-
- 2.2.1 直接选择排序
- 2.2.2 堆排序
- 2.3 交换排序
-
- 2.3.1 冒泡排序
- 2.3.2 快速排序
- 2.4 归并排序
- 2.5 计数排序
- 3 排序算法的性能评价和小结
-
- 3.1 都有哪些性能评价指标
- 3.2 总结
1 什么是排序以及排序算法的分类
1.1 排序的概念
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
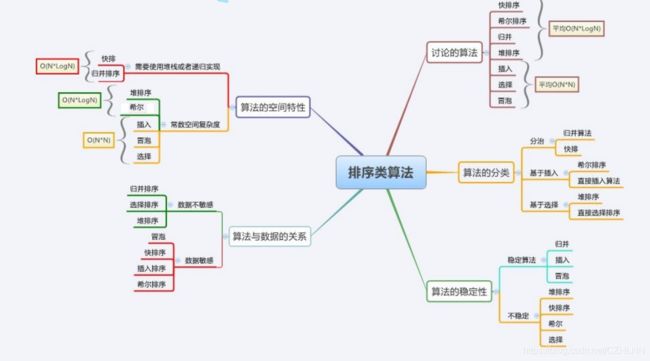
1.1 排序的分类
2 都有哪些排序算法
2.1 插入排序
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一
个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想。

2.1.1 直接插入排序
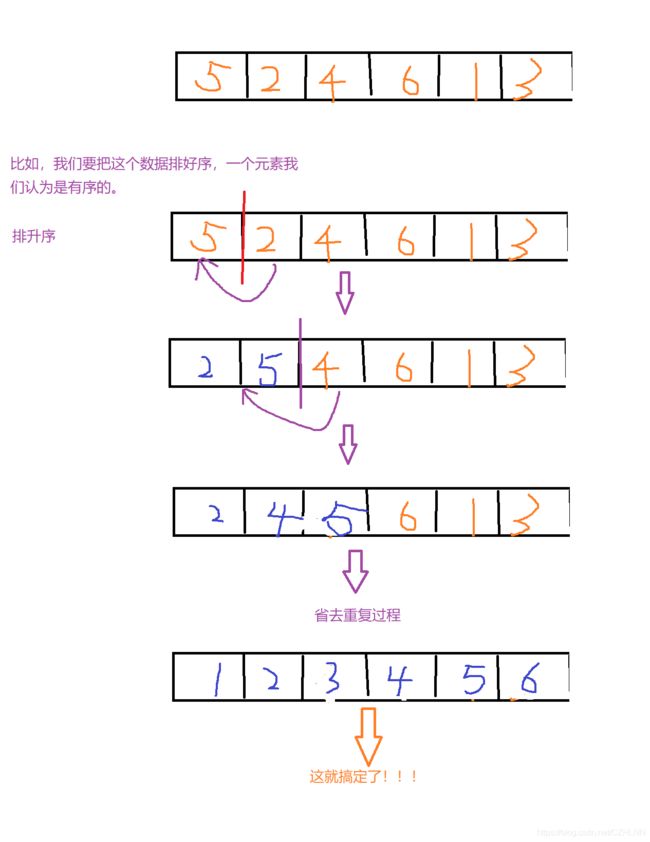
当插入第i(i>=1)个元素时,前面的array[0],array[1],、、、array[i-1]已经排好序,此时用array[i]与arr[i-1]、array[i-2]、、、、进行比较,找到插入的位置将array[i]插入,原来位置上的元素后移。
为了更好的说明问题,看下图
代码实现:
void InsertSort(int* arr, int n)
{
assert(arr);
//排升序
//把[0,end] 把下标为end+1的元素往里面插,则end最大为倒数第二个,endMin = 0,endMax = n-2;
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end>=0)
{
if (tmp < arr[end])
{
//向右移动数据
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}
特性:
1、元素结合越接近有序,直接插入排序算法的时间效率就越高。
2、时间复杂度
最好的情况是比如升序,恰好数据就是升序的此时不用移动数据直接在后面插入即可:O(N)
最坏的情况是逆序,比如排升序数据却是降序,需要每次移动数据从代码也能看出来是:O(N^2)
3、空间复杂度,不需要借助辅助空间:O(1)
4、稳定性:稳定(稳定性的概念在后面的章节)
2.1.2 希尔排序
希尔排序又称缩小增量法。希尔排序的基本思想是:先选定一个整数gap,把待排序数组中的所有数据分成整数gap组,所有距离为gap的数字被分到了一个组,对没一组内的数据进行插入排序,对全部数据分组排序完,缩小gap,重复上述过程,此时全部数据已经接近有序,此时gap==1,进行真正的插入排序,因为此时的数据已经接接近有序,所以直接插入排序的效率就很高。
为了更加清晰明了说明问题我做了下图:

代码实现:
//希尔排序
void ShellSort(int* arr, int n)
{
assert(arr);
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}
特性
1、希尔排序是对直接插入排序的优化。
2、当gap>1时都是预排序,目的是让数据接近有序。当gap==1时,数组已经接近有序了,这样就会很快。这样整体而言就会达到优化的效果。
3、其时间复杂度不好计算,为O(N1.3)到O(N2)
4、空间复杂度为O(1),因为没有借助辅助空间
5、稳定性:不稳定
因为在分组的时候可能会把相同的元素分到不同的组中,在进行排序时不能保证相同元素的相对顺序。
2.2 选择排序
每次从待排序的数据序列中选出最大(或者最小)的数据,放在序列的起始位置或者末尾位置,直到全部排序的数据元素排完。
2.2.1 直接选择排序
因为选择排序的思想很简单,所以不过多解释。直接干图
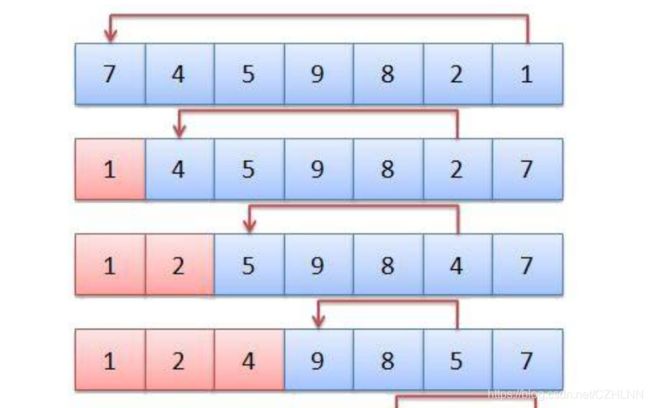
代码实现:
升级版本:一次选两个数一个最大一个最小
简单版本:一次选一个最大或者最小
//1、直接选择排序 ---升级版-----每次选两个数一个最大的,一个最小的 vvvvvvvvvvvvvvv
void SelectSort1(int* arr, int n)
{
int begin = 0, end = n - 1;
//在[begin,end]中最大数和最小数
while (begin < end)
{
int mini = begin;
int maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
Swap(&arr[begin], &arr[mini]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&arr[end], &arr[maxi]);
begin++;
end--;
}
}
void SelectSort2(int* arr, int n)
{
assert(arr);
//[0,end]中找到一个最大的数,和数组最后的元素交换
int end = n - 1;
while (end > 0)
{
int maxi = 0;
for (int i = 1; i <= end; i++)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
//程序走到这里选出一个最大的数
//交换最大的数和最后的数
Swap(&arr[maxi], &arr[end]);
end--;
}
}
直接选择排序的特性:
1、思想简单,效率低,很少用。
2、时间复杂度:O(N^2)
3、空间复杂度:O(1),因为没有借助辅助空间。
4、稳定性:不稳定。
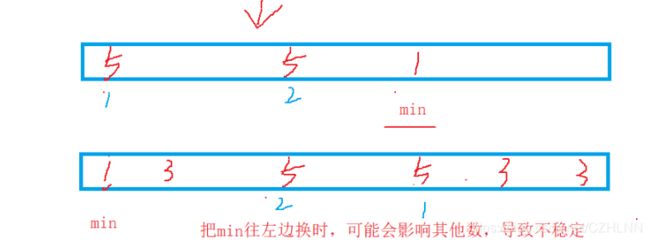
要想明白不稳定的话其实可以举个反例。
2.2.2 堆排序
这里不介绍了哦,之前写过一篇堆的文章里有堆排序,https://blog.csdn.net/CZHLNN/article/details/112481962
理解堆排序的关键是完全二叉树的顺序存储和向下调整算法。
特性总结:
1、堆排序使用堆来选择数,效率就高很多。
2、时间复杂度:O(N*logN)
3、空间复杂度:O(1)
4、稳定性:不稳定
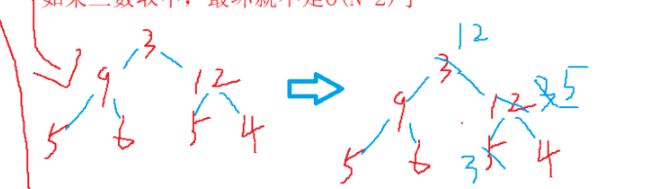
两个5之前的相对顺序在排序后改变了,所以不稳定。
这里我想写一个关于堆的应用,求TopK问题,假设硬盘里有10亿个数字序列,求最小的前10个数。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//topk问题
//思路:求最小的前K个数,建前k个数的大堆,从第k+1个数开始和堆顶的数据比较比堆顶小的就替换堆顶的数据,直到把所有的数据都遍历完
//这个堆里面的数据就是最小的前K个,堆顶的数据就是第k个数据。
//同理如果是求最大的前K个数,是建小堆
void AdjustDown(int* arr,int n,int root)
{
int parent = root;
int child = 2*parent +1;
while(child<n)
{
if(child+1<n && arr[child+1]>arr[child])
{
child++;
}
if(arr[child]>arr[parent])
{
int tmp = arr[child];
arr[child] = arr[parent];
arr[parent]=tmp;
parent = child;
child = 2*parent+1;
}
else
{
break;
}
}
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
//1、建前k个数的大堆
*returnSize = k;
if(k==0)
{
return NULL;
}
int* retArr = (int*)malloc(sizeof(int)*k);
//把原始数据中前k个数放进retArr中
for(int i = 0;i<k;i++)
{
retArr[i] = arr[i];
}
//建大堆
for(int i = (k-1-1)/2;i>=0;i--)
{
AdjustDown(retArr,k,i);
}
//2、建完堆后开始和原始数组中的数据进行比较
for(int i = k;i<arrSize;i++)
{
if(arr[i]<retArr[0])
{
retArr[0]=arr[i];
AdjustDown(retArr,k,0);
}
}
return retArr;
}
2.3 交换排序
基本思想:所谓交换,就是跟根据数据序列中两个记录键值的比较结果,交换两个位置的键值,将键值较大的记录向尾部移动,键值较小的记录向序列的前部移动。
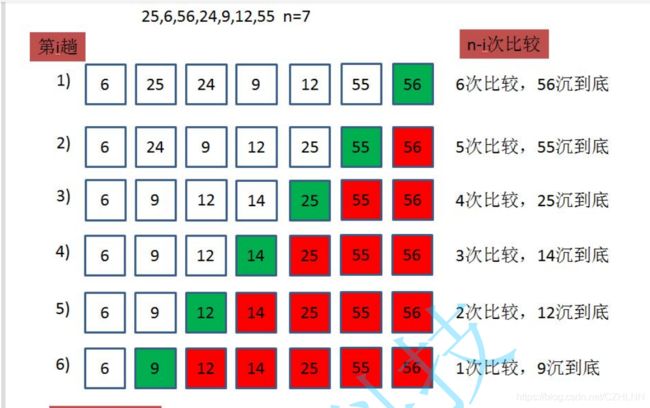
2.3.1 冒泡排序
//冒泡排序
void BubbleSort(int* arr, int n)
{
assert(arr);
int end = n;
while (end > 1)
{
int exchange = 0;
for (int i = 1; i < end; i++)
{
if (arr[i]>arr[i - 1])
{
Swap(&arr[i], &arr[i - 1]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
end--;
}
}
特性:
1、时间复杂度:O(N^2)
2、空间复杂度:O(1),因为没有借助额外的空间
3、稳定性:稳定
2.3.2 快速排序
快速排序是C/C++库中排序函数的实现方式。
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,基本思想是:任取排序元素序列中某元素作为基准值,按照该元素的值将待排序集合分成两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,比如[0,end]选出中间的div则变为[0,div-1] div [div+1,end]。左右子序列重复该过程,直到所有元素都排列在相应的位置上。
将区间按照所选的基准值划分为左右两半部分的常见方式有:
1、hoare版本(左右指针法)
//左右指针法
int PartSort1(int* arr, int begin, int end)
{
assert(arr);
//三数选中优化
int mid = GetMidIndex(arr, begin, end);
Swap(&arr[mid], &arr[end]);
int keyIndex = end;
while (begin < end)
{
//左边找比key大的值
while (begin < end && arr[begin] <= arr[keyIndex])//等号必须要带否则可能死循环
{
begin++;
}
//右边找比key小的值
while (begin < end && arr[end] >= arr[keyIndex])//等号必须要带否则可能死循环
{
end--;
}
Swap(&arr[begin], &arr[end]);
}
//出循环后begin == end是一个位置
int div = begin;
Swap(&arr[div], &arr[keyIndex]);
return div;
}
2、挖坑法
//挖坑法(挖坑法和双指针法相似,但是前后指针法不太一样)
int PartSort2(int* arr, int begin, int end)
{
assert(arr);
int mid = GetMidIndex(arr, begin, end);
Swap(&arr[mid], &arr[end]);
//选出key作为坑
int key = arr[end];
while (begin < end)
{
//排升序从左开始找比key大的数,直接放到坑里。
while (begin < end && arr[begin] <= key)
{
begin++;
}
arr[end] = arr[begin];
//begin的坑(位置空出来了)等待从右向左找的比key小的数填上
while (begin < end && arr[end] >= key)
{
end--;
}
arr[begin] = arr[end];
}
arr[begin] = key;
return begin;
}
3、前后指针法
//前后指针法(较难理解画画图就理解了)
int PartSort3(int* arr, int begin, int end)
{
assert(arr);
int prev = begin - 1;
int cur = begin;
//还是要进行三数选中进行优化
int mid = GetMidIndex(arr, begin, end);
Swap(&arr[mid], &arr[end]);
int keyIndex = end;
while (cur < end)
{
if (arr[cur] < arr[keyIndex] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
Swap(&arr[++prev], &arr[keyIndex]);
return prev;
}
而且快速排序可以用递归的方法写,也可以用非递归的方法写。
1、递归版本
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
//小区间优化,当区间长度<10,区间内元素已经接近有序,可以使用插入排序进行优化
if (right - left > 10)
{
int div = PartSort2(arr, left, right);
QuickSort(arr, left, div - 1);
QuickSort(arr, div + 1, right);
}
else
{
InsertSort(arr + left, right - left + 1);
}
}
2、非递归版本
需要借助栈这个数据结构的先进后出的特性,模拟实现递归的过程。
非递归相比于递归的优势:
1)提高效率(递归建立栈帧还是有消耗的,但是对于现代的计算机,这个优化微乎其微可以忽略不计)
2)递归最大缺陷是,如果栈帧的深度太深,可能会导致栈溢出。因为系统栈空间一般不大在M级别,用栈这种数 据结构来模拟递归,数据是存储在堆上的,堆是G级别的空间,足够大去折腾
代码实现:
//过程和二叉树的递归遍历相似
//把要操作的区间下标存在栈中
void QuickSortNonR(int* arr, int left, int right)
{
assert(arr);
Stack st;
StackInit(&st);
//非递归代码
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int div = PartSort2(arr, begin, end);
//[begin, div-1] div [div+1, end]
if (div + 1 < end)
{
StackPush(&st, end);
StackPush(&st, div + 1);
}
if (begin < div - 1)
{
StackPush(&st, div - 1);
StackPush(&st, begin);
}
}
StackDestory(&st);
}
特性总结:
1、快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序。
2、时间复杂度:O(N*logN)
3、空间复杂度:O(logN)
4、稳定性:不稳定
2.4 归并排序
基本思想:归并排序是建立在归并操作上的一种有效的排序算法,该算法采用分治法的一个典型的应用。将已经有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。把两个有序表合并成一个有序表,称为二路归并。
过程如图所示:
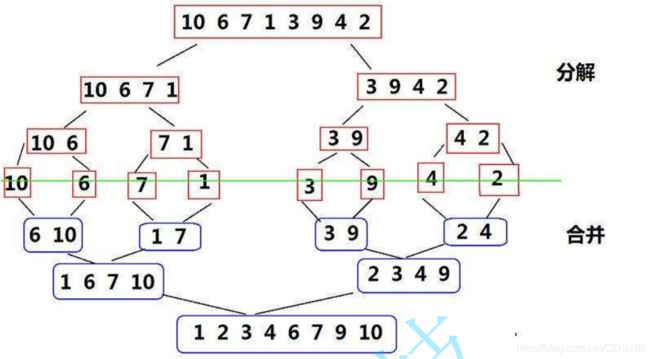
需要和原数组相同大小的辅助空间来操作。
代码实现:
1、递归实现
void MergeArr(int* arr, int begin1, int end1, int begin2, int end2, int* tmp)
{
int left = begin1;
int right = end2;
//保存begin1和end2是为了最后拷数据的时候有首尾下标
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
//走到这里较短的区间肯定处理完了,把较长区间剩下的有序数据放到tmp中
//因为不知道哪个区间是先处理完的,所以两个区间都拷贝一下
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//把tmp的数据拷贝到原数组
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
void _MergeSort(int* arr,int left, int right,int* tmp)
{
//不断拆分直到不能再拆分
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//[left,mid][mid+1,right]
//这个递归过程是拆分的过程
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
//这是把两个有序的区间合并成一个有序的区间的过程,即归并过程
MergeArr(arr, left, mid, mid + 1, right, tmp);
}
// 归并排序递归实现
void MergeSort(int* arr, int n)
{
assert(arr);
int* tmp = (int*)malloc(sizeof(int)*n);
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
}
2、非递归实现
//归并排序非递归实现(这个需要再重新看一下)
void MergeSortNonR(int* arr, int n)
{
assert(arr);
int* tmp = (int*)malloc(sizeof(int)*n);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//合并时只有第一组,第二组不存在就不需要合并
if (begin2 >= n)
{
break;
}
//如果第二组只有部分数据需要修正end2的边界为n-1
if (end2 >= n)
{
end2 = n - 1;
}
MergeArr(arr, begin1, end1, begin2, end2, tmp);
}
gap *= 2;
}
free(tmp);
}
特性
1、归并的缺点是在于需要O(N)的时间复杂度,归并排序的思考更多的是解决磁盘中的外排序问题。
2、时间复杂度:O(N*logN)
3、空间复杂度:O(N)
4、稳定性:稳定
2.5 计数排序
计数排序是为数不多的非比较排序,又称为鸽巢原理,是对哈希定址法的变形应用。操作步骤:
1、统计相同元素出现的次数
2、根据统计的结果将序列回收到原来的序列中。
代码实现;
//计数排序
//计数排序在数据分布密集,最大最小值的差距不是很大的时候的效率很高
void CountSort(int* arr, int n)
{
assert(arr);
//遍历数组找到最大值和最小值
int max = arr[0];
int min = arr[0];
for (int i = 1; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
int range = max - min + 1;
int* countArr = (int*)malloc(sizeof(int)*range);
memset(countArr, 0, sizeof(int)*range);
//arr[i]-min是countArr中的下标
//在countArr数组中统计出arr数组中数字出现的次数
for (int i = 0; i < n; i++)
{
countArr[arr[i] - min]++;
}
//把countArr中的数据对照着复制给arr
int index = 0;
for (int j = 0; j < range; j++)
{
while (countArr[j]--)
arr[index++] = j + min;
}
free(countArr);
}
特性:
1、计数排序在数据范围(最大值与最小值之差)集中时,效率很高,但是使用范围及场景有限。
2、时间复杂度:O(max(N,范围))
3、空间复杂度:O(范围)
4、稳定性:稳定
3 排序算法的性能评价和小结
3.1 都有哪些性能评价指标
时间复杂度
空间复杂度
稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次
序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
3.2 总结
完整代码请点击这里
https://github.com/CZH214926/C_repo