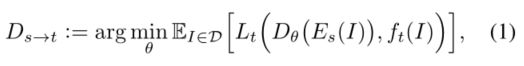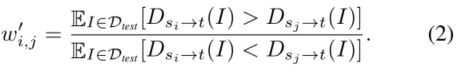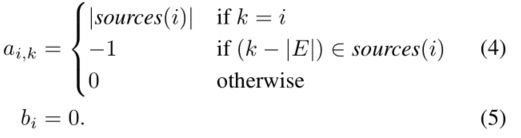【论文学习记录】Taskonomy: Disentangling Task Transfer Learning
这篇是CVPR 2018的best paper，论文原文《Taskonomy: Disentangling Task Transfer Learning》。主要是研究视觉任务之间的关系，根据得出的关系可以帮助在不同任务之间做迁移学习。
作者首先提出视觉任务之间是否有关系？还是他们是相互独立的？其实我觉得迁移学习之所以可行，其实是默认了任务之间是有关系的，所以答案当然是肯定的。
传统大多尝试将视觉任务逐一击破。这种方法造成了两个问题：第一， 逐一击破需要为每一项任务收集大量数据，随着任务数量的增多，这将会是不可行的；第二，逐一击破会带来不同任务之间的冗余计算和重复学习。所以希望能有效测量并利用视觉任务之间的关联来避免重复学习，从而用更少的数据学习我们感兴趣的一组任务。
Taskonomy（task taxonomy）是一项量化不同视觉任务之间关联、并利用这些关联来最优化学习策略的研究。如果两个视觉任务A、B具有关联性，那么在任务A中习得的representations理应可为解决任务B提供有效的统计信息 。作者通过迁移学习计算了26个不同视觉任务之间的一阶以及高阶关联。
Taskonomy方法分为两个大阶段，四个小步。
第一大阶段涉及前三小步，量化不同视觉任务之间的关联，并将任务关联表达成一个affinity matrix（关联矩阵）。第二大阶段，也就是最后一步，对求得的affinity matrix进行最优化，求得如何最高效地去学习一组任务。这个最高效的策略会由一个指向图 (directed graph) 来表示，称此指向图为Taskonomy。
下面看一下怎么来描述这个问题。
在有限的监督预算
下最大化在一组目标任务 (target tasks)
上的表现。同时，有一组起始务 (source tasks) S，其定义为可从零学习的任务。监督预算 的定义为多少起始任务愿意从零开始学习。 
代表感兴趣但不能从零学习的任务，比如一个只能有少量数据的任务。
代表不感兴趣但可以从零学习的任务。
代表感兴趣也能从零学习的任务，但因为从零学习会消耗监督预算，我们希望从中选择出符合预算的一组从零学习，余下的通过少量数据的迁移学习来实现。称
为任务词典 (task dictionary)。最后，我们对视觉任务
的定义为一个基于图片的方程
。
作者收集了一个有四百万张图片的数据集，每张图片均有26个不同视觉任务的标注(ground truth)。这26个任务涵盖了2D的、3D的和语义的任务，构成了本项research的任务词典。因为这26个任务均有标答，S也为这26个任务。
下面过一下两大阶段的四个小步。
一、从零开始学习
为每一个任务训练一个单独的神经网络。为了能更好地控制变量从而比较任务关联，每个任务的神经网络具有相似的encoder decoder结构。所有的encoder都是相同的类ResNet 50结构。因为每个任务的output维度各不相同，decoder的结构对不同的任务各不相同，但都只有几层，远小于encoder的大小。
二、迁移学习
给定一个起始任务
和一个目标任务
，将以 s 的统计计算作为输入来学习 t 。则学习目标是Readout function
最小化损失
。
其中，
是图像I在encoder s的统计表达，
是图像I关于任务t的ground truth。
对于所有s和t组合，均训练了一个。对于t，不同的 会对 的表现造成不同的影响。更具关联的s会为t提供更有效的统计信息；相反不具备关联的s则并不能有此表现。因此，作者认为 在t任务中的表现可以很好地代表了s之于t的关联性。
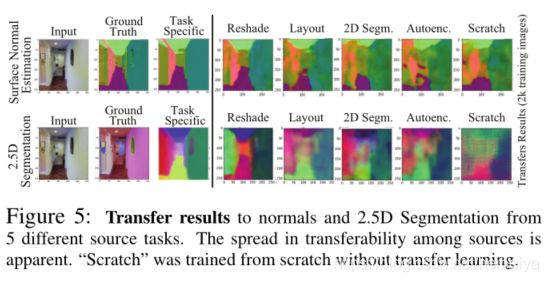
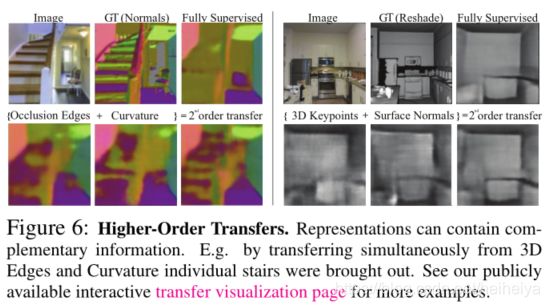
除了上述一阶关联，作者还研究了高阶关联，就是几个任务之间可能具有互补性，结合几个起始任务会对解决目标任务起到帮助，就是多对一的关联。因为高阶的任务组合数量太大，作者基于一阶表现选择了一部分的组合进行迁移学习。对于小于五阶的高阶，作者根据一阶的表现，将前五的所有组合作为输入。对于n>5阶，作者们选择结合一阶表现前n的起始任务作为输入。
三、序数归一化Ordinal Normalization
这一步的目标为用一个 affinity matrix 量化任务之间的关联。虽然在迁移网络中获得了很多的loss 
，但是因为这些loss来自不同的网络使用的是不同的loss函数，因此它们的值域差别很大。直接使用这些loss来构建 affinity matrix会导致矩阵内的值分布极其不均匀，不能有效反应任务之间的关联。同时，简单的线性规范化也并不能解决问题，因为任务的loss值和表现并不构成线性关系。因此，作者采用Ordinal Normalization（基于序数的规范化）来将loss值转换为关联度。该方法基于运筹学中的 AHP (Analytic Hierarchy Process)。概括来讲，affinity matrix中的第（i，j）个值为利用第i 个起始任务迁移后，其网络有多大的几率表现好于用第j个网络。
对于每个目标任务t，构建成对的矩阵
，其值在[0.001，0.999]之间，服从拉普拉斯平滑，其纵轴和横轴均对应所有的起始任务及我们计算过的高阶组合。给定一个测试集
， 的（i，j）项为
在 的所有图片输入中有多大的几率表现好于
，计算
，
的（i，j）项 
现在代表着 表现好于几倍。这样：
在把 规范化成数值和为1的矩阵后，将 相对于t的关联性（或者可迁移性）定义为的第i项principal eigenvector。将所有目标任务的合并起来，我们获得最终的affinity matrix P。
四、计算全局Taxonomy
最后要基于affinity matrix求得如何最有效地学习一组我们感兴趣的任务。
选择一些任务从零学习，剩下的任务用少量数据进行迁移学习，具体迁移学习的策略由subgraph中的edge来决定（对一条directed edge，起始点代表从零学习的一个任务，终点代表要进行迁移的目标任务）。因此，可以通过解如下BIP最优化问题来得到最优解：
迁移的每个元素
是其目标任务的重要性和迁移性能的乘积：
所有目标的集体表现是他们各自的AHP表现pi的总和，由用户指定的重要性ri加权。
要解决最优解有三个限制条件：
1. 如果选择了一个迁移，那么迁移的起始任务（可能为高阶起始集）和目标任务均要出现在subgraph中；
2. 每个目标任务有且仅有一个迁移（将从零学习在途中定义为从自己到自己的迁移，即一条自己到自己的edge）；
3. 不超过监督预算。
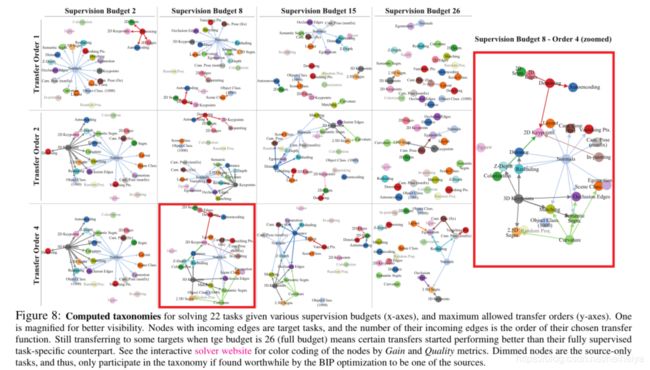
下图是作者解最优subgraph selection从而获得了最有效迁移学习策略。
