LeetCode题解——142. 环形链表 II

题目相关

题目链接

LeetCode中国，https://leetcode-cn.com/problems/linked-list-cycle-ii/。

题目描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例

示例1

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例2

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例3

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

进阶

你是否可以不用额外空间解决此题？

题目分析

LeetCode 给出本题难度中等。是学习数据结构链表的基础题目。本题是 141 的升级版本。141 只需要找有没有环，142 需要找出环的起点。所以本题包含了两个子问题：

子问题 1：链表中有环。

子问题 2：找到环的起点。

样例数据分析

样本数据是否有环，已经在 141 的题解报告中分析过，链接为：https://blog.csdn.net/justidle/article/details/106438974。这里我们用图解来分析，如何找到环的起点。样本数据继续使用样例数据 1。

初始状态

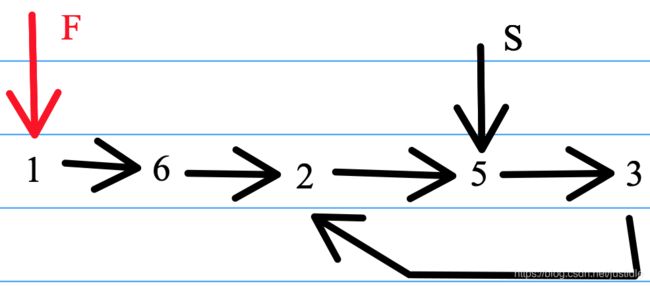
我们已经确定有环。如下图所示。

那么，我们将快指针（fast）指向链表的头指针，这样对应的指针状态如下图所示。

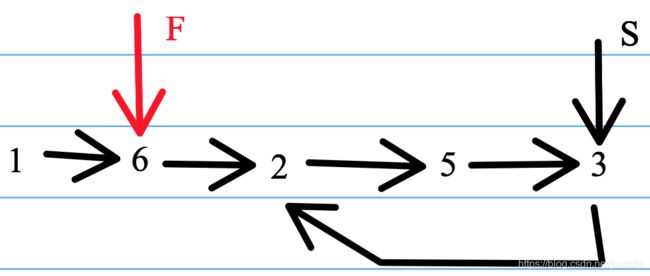
下面我们快慢指针的移动策略变为同速，也就是快慢指针都每次向后移动一位。由于样例数据只需要移动一下就找到环的起点。我们改用下面的样例来说明。

2、由于慢指针（slow）和快指针（fast）不相等。我们将慢指针（slow）和快指针（fast）各自向后移动一位。如下图所示。

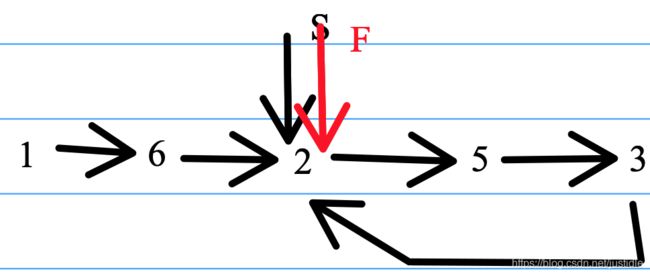
3、由于慢指针（slow）和快指针（fast）不相等。我们将慢指针（slow）和快指针（fast）各自向后移动一位。如下图所示。

4、如上图所示，我们发现两个指针重合，这样我们就找到了环的起点。

数学相关

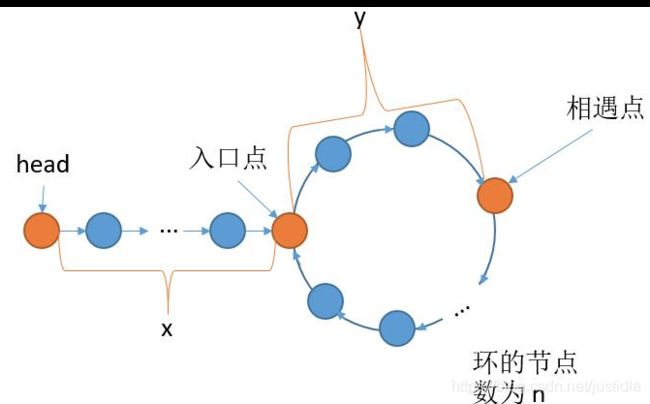
其实在相关的数据结构教程中，已经证明了这个方法的可行性。如下图所示的数据结构。

 

设快慢指针第一次相遇时，慢指针移动距离为 ，快指针移动距离为 。

进过变换我们可得：

左边的含义是从 head 到达入口点；右边的含义，n-y 就是相遇点到入口点的距离， 就是转  圈。
也就是说，从相遇点走到入口点，然后转  圈后再次回到入口点的这段时间内，刚好就等于从 head 走向入口点的时间。

AC 参考代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        //特例判断
        if (NULL==head) {
            return NULL;
        }
 
        ListNode *slow = head;//慢指针
        ListNode *fast = head;//快指针
        while (NULL!=fast && NULL!=fast->next && NULL!=fast->next->next) {
            //修改位置
            slow = slow->next;
            fast = fast->next->next;
            //判断有环
            if (slow==fast) {
                fast = head;
                while (slow!=fast) {
                    fast = fast->next;
                    slow = slow->next;
                }
                return fast;
            }
        }

        //无环
        return NULL;
    }
};