离散时间信号处理/Week1

离散时间信号处理/Week1

教材：Oppenheim离散时间信号处理（第三版） 课程：MITx 6.341x（来源于edX）

edX学习资料地址：https://courses.edx.org/courses/course-v1:MITx+6.341x_2+2T2016/course/

第一周课程学习整理如下

Unit 1: Signals and systems in the time and frequency domains

---

特别关注：差分方程如何与系统的脉冲响应相关联

---

概览

三个非常重要的，将在整个课程中使用相当多的主题：

1. LTI系统的差分方程
2. 频率响应幅度、振幅、相位和群延迟
3. 对窄带和宽带信号群延迟的解释
   

---

特别关注：差分方程如何与系统的脉冲响应相关联

关联并不是直接的，例如：有限脉冲响应可以被描述为递归或者非递归的差分方程；一个线性差分方程可以对应多个不同的脉冲响应，有时甚至会导致一个非线性的系统，这取决于初始条件。

为何了解相位： 我们已经熟悉了系统的频率响应幅度如何影响信号。例如通过一个因果性的LTI系统来处理我的语音，它的频率响应幅度恒定，而相位响应则是一种频率的极端非线性函数。所以一个LTI系统，它的幅度响应和简单的游戏一样，但相位响应却大不相同。

一、LTI系统的差分方程

1. 引言

一大类LTI系统的输入输出关系用线性常系数差分方程(LCCDE)来表征。LCCDE几个特性：

LCCDE本身并不能为任何给定的输入指定唯一的输出，因为输出包含齐次解。具体的解可以通过明确的边界条件，如初始条件或初始静止条件来确定，或者更隐含地通过另外指定系统是LTI和因果的或LTI和稳定的，或者它是LTI，脉冲响应（即系统函数）的z-变换有指定收敛区域（ROC）

LTI系统可以是FIR（有限脉冲响应）或IIR（无限脉冲响应）系统。当然无论哪种情况下，脉冲响应都是从-∞延伸到∞，但如果是FIR系统，那么只有有限的脉冲响应值是非零的。

以LCCDE为特征的LTI系统可以是递归式或非递归式的。递归方程意味着当前输出的计算递归地依赖于以前的输出值，当然也依赖于输入值。非递归意味着当前值的计算直接依赖于有限数量的输入值，而不是之前的输出值。

对于IIR LTI系统，LCCDE总是递归的。然而FIR系统也可以用递归差分方程来实现，这实际上是在传递函数中加入了极零消除。

鼓励阅读教材第2章第2.1至2.4节，特别是仔细阅读文中的第2.5节。

2. 教材2.1-2.5、5.2

(其余相关内容见离散时间信号处理/Week1_Appendix
含教材第二章离散时间信号与系统、第三章z变换部分内容)

2.1 离散时间信号

基本概念：采样周期、单位样本序列（离散时间脉冲、脉冲）、频率、相位

n总是整数——导致离散时间复指数和正弦序列与连续时间复指数和正弦信号之间的重大区别：

• 考虑一个频率为（${\omega }_0$+2$\pi$）的序列，$$x[n]=A{e}^{j({\omega }_0+2\pi )n}=A{e}^{j{\omega }_{0}n}$$
  频率为（${\omega }_0$+2$\pi r$）的复指数序列（r为任意整数）相互间无法区分，这一点对正弦序列也成立。
  当讨论具有$x[n]=A{e}^{j{\omega }_{0}n}$的复指数信号或者具有$x[n]=Acos({\omega }_{0}n+\varphi )$的实正弦信号时，只需要考虑范围为2$\pi$的一般频率就够了，一般取$-\pi <{\omega }_0\le \pi$。
• 关于n的周期性问题：连续时间的正弦信号和复指数信号都是时间上的周期信号，周期等于2$\pi$除以频率。离散时间要求$${\omega }_{0}N=2\pi k$$
  k为整数。如此，复指数和正弦序列对n来说并不一定是周期为$（2\pi /{\omega }_0）$的周期序列，在n上受到整数限制就会引起某些正弦信号根本就表示周期的。
  增大一个离散时间正弦信号的频率${\omega }_0$并不一定就会减小信号的周期。
  结合一个周期序列应满足$x[n]=x[n+N]$和${\omega }_0$和（${\omega }_0$+2$\pi r$）是不可区分的频率，存在N个可区分开的频率，对应这些频率的序列都是周期的，且周期为N。这些频率中的一组就是${\omega }_k=2\pi k/N,k=0,1,...,N-1$。
• 对于连续时间和离散时间正弦和复指数信号的高低频率的解释稍许有些不同：
  $e^{j{\omega }_{0}n}$ 不具有随${\omega }_0$在数值上的增加而不断增加其振荡速率的特性，随着${\omega }_0$从0开始增加，其振荡速率越来越快，直到${\omega }_0=\pi$ 为止，若继续增加${\omega }_0$，振荡速率就会下降，直到${\omega }_0=2\pi$为止，此时又得到${\omega }_0=0$时同样的结果。因此，离散时间复指数的低频部分（也就是慢变化）位于${\omega }_0=0$，±2π，±4π，…附近，高频部分位于${\omega }_0=$ ±π，±3π，…附近，特别值得注意的是$e^{j\pi n}=(e^{j\pi }{)}^n=(-1{)}^n$ ，以至于信号在每一点上都改变符号，产生剧烈振荡。
  

2.2 离散时间系统

概念：理想延迟系统、滑动平均、无记忆系统、线性系统（含累加器系统）、非线性系统（不满足齐次性和可加性）、时不变系统（包含累加器系统）、压缩器系统（为时变系统）、因果性、前向差分系统（非因果）、后向差分系统（因果）、稳定性

2.3 线性时不变（LTI）系统

概念：卷积和

2.4 线性时不变系统的性质

1. 卷积运算满足交换律、相加上满足分配律（用于LTI系统并联连接时等效与一个单一的系统，该系统的单位脉冲响应是各系统单位脉冲响应之和）、结合律（LTI系统课按照任意脉冲响应顺序级联，等效的整体脉冲响应为各脉冲响应做卷积运算）
2. 稳定性：有界输入产生有界输出（BIBO）
   当且仅当单位脉冲响应是绝对可加时，LTI系统才是稳定的，即$$B_h=\sum _{k=-\infty }^{\infty }|h[k]|<\infty$$
3. 因果性：对LTI系统的因果性，下述条件成立：$$h[n]=0,n<0$$将$n<0$时其值为零的序列称为因果序列，因果序列可以作为因果系统的单位脉冲响应。
4. 注意：卷积公式、表示稳定性和因果性的式子不能用于非线性或时变系统

LTI系统的性质如何在它们的单位脉冲响应中得到反映：

5. 通过计算单位脉冲响应的绝对值之和来检查系统的稳定性，对于理想延迟、滑动平均、前后向差分，显然$B_h<\infty$，因为这些单位脉冲响应都只有有限个非零样本。通常情况下，一个具有有限长度单位脉冲响应的系统（FIR系统）总是稳定的。
6. 累加器的单位脉冲响应是无限长的，属于无限长脉冲响应（IIR）系统，单位脉冲响应$h[n]=a^{n}u[n],|a|<1$的系统就是IIR系统中为为稳定系统的一个例子。
7. 累加器和后向差分系统是因果的，而前向差分系统是非因果的。
8. 两个序列之间的卷积运算会带来很多涉及系统问题的简化：

• 一个移位单位样本序列与任何信号$x[n]$的卷积：只需将$x[n]$作相同的移位。
• 非因果前向差分系统通过级联一个延迟系统能将它转换成因果系统。一般来说，任何非因果的FIR系统都能够称为因果的，只要与它级联一个足够长的延迟系统即可。
• 一个累加器后面紧跟着一个后向差分（反之亦然）的级联连接产生一个单位脉冲响应为一个单位样本（即$\delta [n]$）的系统，该级联系统的输出总等于输入。后向差分系统完全补偿（或反演）了累加器的效果，即后向差分系统是累加器的逆系统，由卷积的可交换性，累加器也是后向差分系统的逆系统。

2.5 线性常系数差分方程

对于一个系统，其输入和输出满足一个线性常系数差分方程，则有：

1. 对于一个输入，其输出表示唯一的，需要一些辅助信息和条件。
2. 如果辅助信息一N个顺序输出值的形式给出，则后面的值可以将差分方程重新安排成以n的前向计算的递推关系来求出；前面的值可以将差分方程安排成以n的后向运算的递推关系求出。
3. 系统的线性、时不变性和因果性将依赖于辅助条件，如果一个附加条件是使系统初始松弛的，则该系统就是线性、时不变和因果的。

5.2 用线性常系数差分方程表征方程

离散时间滤波器几乎都是通过形如如下常系数差分方程的形式来实现：$$\sum _{k=0}^N{a}_{k}y[n-k]=\sum _{m=0}^M{b}_{m}x[n-m]$$其系统函数：$$H(z)=\frac{Y(z)}{X(z)}=\frac{{\sum }_{k=0}^M{b}_k{z}^{-k}}{{\sum }_{k=0}^N{a}_k{z}^{-k}}$$也可以表示成如下形式$$H(z)=(\frac{b_0}{a_0})\frac{{\Pi }_{k=1}^M(1-c_k{z}^{-1})}{{\Pi }_{k=1}^N(1-d_k{z}^{-1})}$$分子因式$(1-d_k{z}^{-1})$中的每一项都在$z=c_k$提供一个零点和在$z=0$提供一个极点。类似地，分母因式$(1-d_k{z}^{-1})$中的每一项都在$z=0$提供一个零点和在$z=d_k$提供一个极点。

1. 稳定性和因果性

• 为了从常系数差分方程表达式得到系统函数表达式，曾假设系统是LTI的，但未对稳定性和因果性作假设。从差分方程可得系统函数的代数表达式，但无法得到收敛域（有几种收敛域的选择），使系统函数表达式成立就是要求$X(z)$和$Y(z)$有重合的收敛域，和第2章差分方程不能唯一确定一个LTI系统的单位脉冲响应一致。
• 但若假定系统是因果的，$h[n]$必须是右边序列，此时$H(z)$的收敛域位于最外面极点的外面；若为稳定的，$H(z)$的收敛域包括单位圆。

2. 逆系统

• 系统函数为$H_i(z)$的逆系统与$H(z)$级联后，总的系统函数是1，即$$G(z)=H(z)H_i(z)=1$$，若该系统的频率响应存在，则有$$H_i(e^{j\omega })=\frac{1}{H(e^{j\omega })}$$该逆系统的对数幅度，相位和群延迟都是原系统相应函数的负值，不是每一个系统都有逆系统，例如理想低通滤波器就没有逆系统，也就是说没有任何办法去恢复被理想低通滤波器置到零的（即位于截止频率以上的）频率分量。
• $H_i(z)$的极点就是$H(z)$的零点；反之亦然。 $H_i(z)$和$H(z)$的收敛域必须重合。
• 若$H(z)$是零点在$c_k$的一个因果系统，当且仅当$H_i(z)$的收敛域为$$|z|>ma{x}_k|c_k|$$时，其逆系统是因果的，若要求逆系统稳定，则要求$H(z)$全部的零点必须在单位圆内。
• 当且仅当$H(z)$的零点和极点都在单位圆内，一个稳定因果LTI系统也有一个稳定因果的逆系统，这样的系统称为最小相位系统

3. 有理系统函数的单位脉冲响应
   任何具有一阶极点的、以$z^{-1}$为幂给出的有理函数可以表示成：$$H(z)=\sum _{r=0}^{M-N}{B}_r{z}^{-r}=\sum _{k=1}^N\frac{A_k}{1-D_k{z}^{-1}}$$区分两类系统

• IIR：至少有一个$H(z)$的非零极点未被某个零点抵消，此时$h[n]$不是有限长的
• FIR：$H(z)$除$z=0$外，没有任何极点，即N=0，因此不可能进行部分因式展开。$H(z)$就只是$z^{-1}$的多项式：$$H(z)=\sum _{k=0}^M{b}_k{z}^{-k}$$$h[n]$可直观看出$$h[n]=\sum _{k=0}^M{b}_k\delta [n-k]=\{\begin{array}{rc}{b}_n,& 0\le n\le M\\ 0,& 其他\end{array}$$

3. MITx T1.1: Difference equations for LTI systems

LTI系统中一种重要的子系统，其输入和输出满足N阶线性常系数差分方程（LCCDE），形式为$$\sum _{k=0}^N{a}_{k}y[n-k]=\sum _{m=0}^M{b}_{m}x[n-m]$$

1. 实现中，所需的延迟寄存器的数量是N或M的较大值，而最典型的是，N大于M，所以这就是为什么叫N阶。
2. 如果给定系数$a_k$和$b_m$系统的输入$x[n]$，这个方程是否唯一指定输出？不是。

• 一个原因是，存在整个问题的初始条件。这与同质解有关（可以在任何解的基础上加一个同质解，仍然满足方程），所以这个方程是输入和输出之间的一个约束，而非从输入到输出的映射。
• 怎么让它成为唯一的？指定了一些东西，把同质的解决方案定下来。现在，输入和输出之间有了一个独特的关系。
• 在这种情况下，它是否对应于一个线性系统？它是否对应于一个时不变的系统？
• 除了指定差分方程之外，还告诉你，这个系统是线性的，时不变的，可以断定这个系统是因果关系吗？不可以。能否得出结论，有了这些信息，知道$x[n]$，$y[n]$是唯一指定的吗？不可以。
• 将等式重新写成$$y[n]=-\sum _{k=1}^N{a}_{k}y[n-k]+\sum _{m=0}^M{b}_{m}x[n-m]$$
  只用$y$的过去值、$x$的现在值和过去值，在任何n处生成$y[n]$。那么，它是因果的吗？显然不是，因为如果原方程不是，这个等式与原方程是同一个等式，那么只做了移位变化的等式也不是因果的。
• 对于$N=0$，$$\sum _{k=0}^0{a}_{k}y[n-k]=\sum _{m=0}^M{b}_{m}x[n-m]$$即$$a_{0}y[n]=\sum _{m=0}^M{b}_{m}x[n-m]$$即$$y[n]=\sum _{k=0}^M(\frac{b_k}{a_0})x[n-k]$$这是一种卷积形式，其对应的单位脉冲响应为$$h[n]=\sum _{k=0}^M(\frac{b_k}{a_0})\delta [n-k]$$或$$h[n]=\{\begin{array}{rc}(\frac{b_k}{a_0}),& 0\le n\le M\\ 0,& 其他\end{array}$$显然，单位脉冲响应为有限长。
  任何FIR系统的输出都能非递推地计算出来，且式中的系数就是单位脉冲响应序列的值。

T1.1清单

• 差分方程规定了系统输入和输出之间的约束条件，但不是输入到输出的映射。

• 由线性恒定系数差分方程（LCCDE）约束的系统不一定是LTI系统。

• 对于一个给定的LCCDE和系统输入，输出不是唯一指定的，因为总是可以添加一个同质解。

• 辅助条件如初始松弛或初始条件可以指定同质解，在这种情况下，输出将是唯一的。

• 如果系统输入和输出由线性常系数差分方程约束，并且系统被指定为LTI，那么给定输入的响应仍然不是唯一的，需要额外的信息。

• 如果系统输入和输出满足LCCDE，并且系统已知是LTI和因果关系（或LTI和稳定），那么对于给定输入的响应是唯一的。

• 一个LTI系统可以是FIR或IIR，这取决于脉冲响应是有限长度还是无限长度。FIR系统也是IIR但只有有限的非零值。

• FIR系统的差分方程可以是递归式或非递归式的。

• 非递归差分方程总是对应于FIR系统，而递归差分方程不一定意味着系统是IIR系统。

二、频率响应幅度、振幅、相位和群延迟

1. 引言

通常在研究LTI系统的频率响应时，我们会分别考虑频率响应幅度和频率响应相位的影响。振幅通常很容易解释，特别是当系统是一个频率选择滤波器或均衡器时。系统相位响应的影响通常较难解释，原因有很多：包括相位是以2π为模数计算的。此外，如果频率响应在任何频率上过零，当使用幅度/相位表示时，会导致π的相位不连续。

在本专题中，我们探讨了表示和解释相位的其他方法。为了避免频率响应通过零时引入的相位不连续，我们引入了幅度/相位表示法。此外，我们还引入了相位“去卷绕”（unwrapping）的概念，以消除通过计算相位模数2π引入的不连续性。在振幅/相位表示法中进行相位去卷绕后，相位将在ω=0和ω=π之间成为频率的连续函数。
即使在振幅/相位表示中进行了相位去卷绕，频率响应相位对输入信号的影响也很难解释。通过考虑卷绕相位的导数或等价的群延迟，可以得到更有意义的解释。在主题1.2中，当群延迟为常数时，群延迟被定义和解释，这对应于线性相位。专题1.3讨论了非线性相位的影响，它对应于非恒定的群延迟。

教材中第5.1节讨论了 "卷绕"与 "去卷绕"相位的概念，以及群延迟的定义和一些影响。第5.1节中的一些讨论也许在专题1.3之后会更有意义，但初步看一下第5.1.2节可能会对专题1.3中的讨论有所帮助。

2. 教材5.0-5.1、5.3

5.0 引言

第二章建立了离散时间信号与系统的傅里叶变换表示，第三章推广至z变换，这两章重点在变换本身及其性质上。第五章建立利用傅里叶变换和z变换来表示和分析LTI系统。
频率响应是系统函数在单位圆上的取值，而系统函数则更一般地作为复变量$z$的函数。从频率响应和系统函数能够容易推出系统的很多性质，两者在LTI系统的分析和表示中都极为有用。

5.1 LTI系统的频率响应

5.1.1 频率响应相位和群延迟

系统的输入输出的傅里叶变换的幅度和相位联系：$$|Y(e^{j\omega })|=|H(e^{j\omega })|\cdot |X(e^{j\omega })|$$$$\angle Y(e^{j\omega })=\angle H(e^{j\omega })+\angle X(e^{j\omega })$$$\angle H(e^{j\omega })$为系统的香味相应或相移，$$\angle H(e^{j\omega })=ARG[H(e^{j\omega })]+2\pi r(\omega )$$
连续相位函数$arg[H(e^{j\omega })]$超出了$-\pi$到$\pi$的范围。若将相位曲线纳入主值范围内，必须在某些区域减去整数倍的$2\pi$，故具有$2\pi$一跳的特点。
相位另一种特别有用的表示形式是通过定义群延迟：$$\tau (\omega )=grd[H(e^{j\omega })]=-\frac{d}{d\omega }arg[H(e^{j\omega })]$$为了解一个线性系统相位，特别是群延迟的影响，首先考虑理想延迟系统$$h_{id}[n]=\delta [n-n_d]$$频率响应是$$H_{id}(e^{j\omega })=e^{-j\omega n_d}$$有$$arg(\omega )=-\omega n_0,|\omega |<\pi$$频率响应是周期的，周期为$2\pi$，时延（或者是超前，如果$n_d<0）$与相位有关，而相位是频率的线性函数。
延迟失真被认为是相位失真的一种很轻微的形式，因其影响只是在序列时间上的移位，在设计近似理想滤波器或其他LTI系统时，往往用线性相位响应而不是零相位响应作为理想模型。如一个具有线性相位的理想低通滤波器：$$H_{lp}(e^{j\omega })=\{\begin{array}{rc}{e}^{-j\omega n_d},& |\omega |<{\omega }_c\\ 0,& {\omega }_c<|\omega |\le \pi \end{array}$$响应的单位脉冲响应是$$h_{lp}[n]=\frac{sin{\omega }_c(n-n_d)}{\pi (n-n_d)},-\infty <n<\infty$$
群延迟给出了对相位线性度的方便度量。下面考虑一个系统频率响应为$H(e^{j\omega })$，对窄带输入$x[n]=s[n]cos({\omega }_{0}n)$的系统输出（见习题5.63），作如下假定：$X(e^{j\omega })$仅在$\omega ={\omega }_0$附近非零，且系统的相位效果在$\omega ={\omega }_0$附近的一个较窄频带内可以近似为表达式：$$arg[H(e^{j\omega })]\approx -{\varphi }_0-\omega n_d$$可证明对$x[n]=s[n]cos({\omega }_{0}n)$的响应近似为$$y[n]=|H(e^{j\omega })|s[n-n_d]cos({\omega }_{0}n-{\varphi }_0-{\omega }_0{n}_d)$$一般地，可以把一个宽带信号看成具有不同中心频率的窄带信号的叠加，如果群延迟$n_d$不随频率变化，则每个窄带分量具有相同的时延。如果群延迟$n_d$不是常数（即相位非线性），不同频率包络$s[n]$有不同的时延，这导致了输出信号能量的时间色散特性。

5.3 有理系统函数的频率响应

如果一个稳定的LTI系统有一有理的系统函数（即输入输出满足常系数差分方程表达式），那么其频率响应（系统函数在单位圆上求值，即$h[n]$的傅里叶变换）具有形式：$$H(e^{j\omega })=\frac{{\sum }_{k=0}^M{b}_k{e}^{-j\omega k}}{{\sum }_{k=0}^N{a}_k{e}^{-j\omega k}}$$$$H(e^{j\omega })=(\frac{b_0}{a_0})\frac{{\Pi }_{k=1}^M(1-c_k{e}^{-j\omega })}{{\Pi }_{k=1}^N(1-d_k{e}^{-j\omega })}$$

5.7 广义线性相位的线性系统

在设计滤波器和其他信号处理系统中，很希望在某一频带范围内频率响应幅度近似恒定和相位为零，使得信号通过这部分频带时不失真。对因果系统，零相位不可能得到，因此必须容许有某种相位失真。具有整数斜率线性相位的影响就是一种单纯的延迟，非线性相位在信号的形状上有很大的影响。下面考虑具有恒定群延迟的一类系统的线性相位和理想时间延迟。

5.7.1 线性相位系统

考虑一理想延迟系统的频率响应$$H(e^{j\omega })=|H(e^{j\omega })|e^{-j\omega \alpha },|\omega |<\pi$$可解释为序列$x[n]$经零相位频率响应$H(e^{j\omega })$滤波，然后将滤波后的输出延迟（或提前）量$\alpha$（整数或非整数）

• 具有线性相位的理想低通滤波器，当$\alpha$为整数时，$\alpha =n_d$，单位脉冲响应对$n=n_d$是对称的，即$h_{lp}[2n_d-n]=h_{lp}[n]$，此时对称点为$\alpha$，此情况可以定义一个零相位系统${\hat{H}}_{lp}(e^{j\omega })=|H_{lp}(e^{j\omega })|$，原来的单位脉冲响应向左移$n_d$个样本，得到一个偶序列$${\hat{h}}_{lp}[n]=\frac{sin{\omega }_{c}n}{\pi n}={\hat{h}}_{lp}[-n]$$
• 若$\alpha$为一个整数再加1/2（或者$2\alpha$为整数）时，此时对称点为$\alpha$，它不是整数。由于对称不是对应序列中的一点，所以要将序列移位还能得到一个具有零相位的偶序列是不可能的。
• 若$\alpha$为其他情况，说明一个单位脉冲响应不是对称的，但具有线性相位，或等效说有恒定群延迟。

5.7.2 广义线性相位

如果系统能表示为$$H(e^{j\omega })=A(e^{j\omega })e^{j\alpha \omega +j\beta }$$就说明该系统是一个广义线性相位系统。这里$\alpha$和$\beta$都是常数，而$A(e^{j\omega })$是$\omega$的实（可正可负）函数，相位由常数项加上线性函数$-\omega \alpha$所组成，即$-\omega \alpha +\beta$是一个直线方程。若忽略相位不连续性，这类系统也可以用恒定群延迟来表征$$\tau (\omega )=\alpha$$更一般的相位形式为$$arg[H(e^{j\omega })]=\beta -\omega \alpha$$线性相位系统的单位脉冲响应在$2\alpha$为整数时，对$\alpha$可以具有对称性，在广义线性相位系统中导出一个对恒定群延迟$h[n],\alpha ,\beta$都必须满足的方程$$\sum _{n=-\infty }^{\infty }h[n]sin[\omega (n-\alpha )+\beta ]=0,对全部\omega （5.130）$$这个方程对于具有恒定群延迟的系统是关于$h[n],\alpha ,\beta$的一个必要条件，它必须对所有$\omega$都成立，但它不是充分条件，并且由于隐含性，没有说明如何去找一个线性相位系统。

• 广义线性相位系统的一类例子满足$$\begin{gathered} \beta =0或\pi \\ 2\alpha =M=一个整数 \\ h[2\alpha -n]=h[n] \end{gathered}$$有了$\beta =0或\pi$，式（5.130）就变成
  $$\sum _{n=-\infty }^{\infty }h[n]sin[\omega (n-\alpha )]=0（5.132）$$可以证明如果$2\alpha$为整数，式（5.132）中各项能配对，每一对求和后对全部的$\omega$都恒定为零,此处$$H(e^{j\omega })=A(e^{j\omega })e^{j\alpha \omega +j\beta }$$$\beta =0或\pi$而$A(e^{j\omega })$是$\omega$的偶（当然也是实）函数
• 另外一类满足$$\begin{gathered} \beta =\pi /2或3\pi /2 \\ 2\alpha =M=一个整数 \\ h[2\alpha -n]=-h[n] \end{gathered}$$有了$\beta =0或\pi$，式（5.130）就变成
  $$\sum _{n=-\infty }^{\infty }h[n]cos[\omega (n-\alpha )]=0$$此处$$H(e^{j\omega })=A(e^{j\omega })e^{j\alpha \omega +j\beta }$$$\beta =\pi /2$而$A(e^{j\omega })$是$\omega$的奇（当然也是实）函数

3. MITx T1.2: Frequency response magnitude, amplitude, phase, and group delay

1. 通过允许振幅为正负摆脱$\pi$的跳变
   $$H(e^{j\omega })=|H(e^{j\omega })|e^{j{\varphi }_M(\omega )}=A(\omega )e^{j{\varphi }_A(\omega )}$$
   幅度（magnitude，即$|H(e^{j\omega })|$）与相位和振幅（amplitude，即$A(\omega )$）与相位之间唯一真正的区别是，在幅度（magnitude）相位描述中，你显然要求幅度是一个非负数，而在振幅（amplitude）相位描述中，振幅可以是正数，也可以是负数。
   注意：在振幅/相位表示法中，振幅是实值，但可以是正值或负值。在幅值/相位表示法中，幅值必须始终是非负值。因此，在振幅为负值的频率上，必须在振幅/相位表示法中通过在相位上添加π的奇数倍来反映。
   
   

   当你在单位圆上绕过0的时候，会得到一个符号的变化，而这个符号的变化会通过$\pi$的跳跃反映在相位特性上。
   所以如果不看幅度和相位，而看振幅和相位，振幅和相位只是简单的排序，当经过了0，这里就是振幅中的负数。但当然，它的幅度必须是正值。所以当你把它整理出来后，你会得到这样一条曲线（第二张图）。所以在振幅相位描述中，这些对应于频率响应通过0的$\pi$的跳变就被剔除了，你允许振幅为正或负。

2. 通过去卷绕摆脱$2\pi$的跳变
   
   上图为振幅相位描述中的卷绕。卷绕可以从$\pi$绕到$-\pi$，或者是从$-\pi$绕到$\pi$。而这原则上很容易解开。为什么这条曲线会有$2\pi$的跳跃？原因当然是，当你用MATLAB或其他计算器进行相位计算时，它将给你的是模为$2\pi$的相位。而很显然，在任何频率下都可以加上$2\pi$的整数倍，而不会改变频率响应的样子。

3. 群延迟
   我们要看的不是相位曲线，而是相位曲线的导数。在谈论相位曲线的时候，$ARG[H(e^{j\omega })]$指卷绕相位（因为对$2\pi$取模的计算可以被想成让相位绕着单位圆环绕），$arg[H(e^{j\omega })]$指去卷绕相位。
   所以群延迟有一个相当简单的定义。它是去卷绕相位对频率的导数的负值，即$$\tau (\omega )=grd[H(e^{j\omega })]=-\frac{d}{d\omega }arg[H(e^{j\omega })]$$除了在不连续点上$ARG[H(e^{j\omega })]$的导数会存在冲激以外，$arg[H(e^{j\omega })]$的导数和$ARG[H(e^{j\omega })]$的导数是相同的。
   注意：$$-{\int }_{-\pi }^{\omega }{\tau }_g(\theta )d\theta =arg(\omega )$$
   如果我有一个信号，它的频率内容高度集中在这个频率附近，那么这个信号会发生什么，如果这是我的系统的输入，输出将是这个信号的大约120个样本延迟。

4. 线性相位与延迟的关系
   考虑一个系统（理想延迟系统）$$H(e^{j\omega })=e^{-j\omega n_0}$$有$$arg(\omega )=-\omega n_0$$$$h[n]=\delta [n-n_0]$$$${\tau }_g(\omega )=n_0$$

• 线性相位
  当一个系统，其幅度相位表示中，相位等于0，意味着脉冲响应是一个偶函数。更广泛地讲，谈论一个脉冲响应，或者一个序列，它的对称性不是围绕着0，而是围绕着其他一些整数值，或者一些非整数值。但我们所说的围绕一个非整数值的对称性是什么意思呢？有一个脉冲响应$h[n]=h[2\alpha -n]$，其中$2\alpha$是一个整数， 那么相位将是线性的，以$\alpha$为斜率。所以在这种情况下，群延迟将是$\alpha$。
• 广义线性相位
  当脉冲响应为奇数对称，考虑$h[n]=-h[2\alpha -n]$，如果$\alpha$等于0，傅立叶变换就不是纯实数，而是纯虚数，故必须添加另一个相位因子$e^{+j\frac{\pi }{2}}$。所以在这种情况下，将有一个频率响应$$H(e^{j\omega })=A(\omega )e^{-j\alpha \omega }{e}^{+j\frac{\pi }{2}}（0<\omega <\pi ）$$振幅为$A(\omega )$，线性相位项为$e^{-j\alpha \omega }$，然后它将被乘以$j$，即添加相位因子$e^{+j\frac{\pi }{2}}$。
• 我们经常会讨论滤波器设计，讨论线性相位系统，广义线性相位系统。我们会讨论群延迟是一个整数的系统。我们会讨论群延迟为非整数的系统。有时我们会讨论群延迟是一个整数加半个整数的系统。有时甚至可以比这更笼统地谈论它。下面给出具有线性相位的理想低通滤波器的例子。
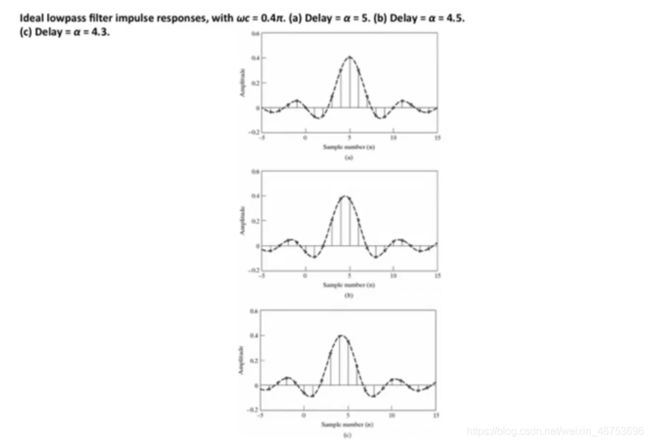
  图中x轴为样本数$(n)$，y轴为振幅。一个是群延迟是整数5，另一个是整数加半整数（4.5），还有一个是以上都不是（4.3）。一个理想的低通滤波器，给一个脉冲激励。如果它是0相位，你会得到一个同步函数；但如果群延迟为5，就会得到一个延迟为5的同步函数；如果是整数加半整数，那么还是有对称性的，但是脉冲响应的对称性在半整数；如果群延迟既不是整数也不是半整数，那么对称性就消失了。
• 从零极点图推断群延迟信息
  

就相位而言，看零向量的相位减去极向量的相位（因为相位响应完全由$H(z)$的零点和极点决定）。在思考群延迟的时候，极向量角度是如何变化的？或者说，当绕着单位圆移动时，相角的角度变化率是多少？当绕着单位圆移动过极点时，导数会发生什么？如果那个极点离单位圆更远或更近，导数会发生什么？接下来要记住的是群延迟是导数的负值。当极向量角度在增加，但是它在分母里。所以它的意思是相位在减小。但是群延迟是相位的导数的负值，所以群延迟是正值。这个极点离单位圆越近，这个角度的变化率就越快。所以当你看零极点的群延迟图时，你希望看到的是，当你越过这个极点时，群延迟会达到峰值。

T1.2 清单：频率响应幅度、振幅、相位和群延迟

• LTI系统的频率响应可以用幅度和相位或幅度和相位来表示。

• 系统的频响相位对输入信号的影响，往往很难从相位图中解释。与群延迟相对应的相位导数的影响，则比较容易解释。

三、窄带和宽带信号的群时延解读

1. 引言

在主题1.2中，线性相位，或者等价于恒定的群延迟，对应于 “时间上的移动”。当然，对于离散时间信号和系统，如果群延迟是恒定的，但不是整数，那么时间上的偏移需要更复杂的解释。

在专题1.3中，我们考虑非线性相位对窄带信号和宽带信号的影响。

窄带信号可以很自然地被看作是一个由单一正弦载波调制的低通包络。通过使用载波频率周围的非线性相位的泰勒级数展开，相位的影响可以解释为载波频率处的群延迟使包络发生 “时移”，载波的时移量称为相位延迟。

宽带信号当然可以解释为许多窄带信号在连续范围的载波频率的叠加。因此，每个窄带频率群在该群的每个中心频率上都会经历与非线性相位相关的群延迟和相位延迟。如果群延迟是非恒定的，即在不同的频率上是不同的，那么不同的频率群将在不同的时间出现在输出端，这对应的是时间色散。例如考虑一个脉冲作为非线性相位的全通系统的输入。该脉冲是窄带频率群的叠加，它们都相干地加在一起形成时间上的脉冲。然而对于非线性相位，不同的频率群一般会有不同的延迟（或提前），因此在时间上会分散。因此，它们将不再在系统输出处叠加成一个脉冲。这种效应在文中的5.1.2节中进行了说明。

符号解析：在课程教材中以及在整个6.341x的大部分时间里，我们用$\omega$来表示离散时间的频率变量，用$\Omega$来表示连续时间的频率变量。在专题1.3中，我们讨论相位为非线性时的群延迟的解释，主要是为了方便进行连续时间系统的讨论，但频率变量用$\omega$表示。

2. MITx T1.3: Interpretation of group delay for narrow-band and wide-band signals

先只关注一个窄带信号$$\begin{gathered} x[n]narrowband：x[n]=s[n]cos({\omega }_{0}n+\theta ) \\ BWofs[n]\ll {\omega }_0 \end{gathered}$$当相位特性是非线性的，不同的频率下有不同的相位，在不同的频率下，斜率也不同。如果信号是窄带的，那么在${\omega }_0$附近，假设我用泰勒展开来逼近相位曲线，所以第0项，这只是值，然后第一阶项，这将捕获相位曲线的斜率。从信号和输出的角度来看，你将无法区分下面这两个系统，换句话说，我只需要通过泰勒系列展开就可以取代$\pm {\omega }_0$下的这个相位，所以这就是基本的想法。可以把这个（下图左下图）看成是两个系统的级联，

等效的两系统级联如下：

所以第一个系统只是表示偏移，这是为了说明原泰勒展开图线与$y$轴交于$+{\varphi }_0$和$-{\varphi }_0$而不是在0处，然后用相位曲线级联，这个相位曲线的斜率是该频率的负群延迟。所以这只是简单的分两块来描述，因为如果我有两个系统级联，级联的相位就是两个系统的相位之和。很明显，相位在系统相乘时是相加的。
那么$H_2(j\omega )$对输入$x_1(t)$做了什么？假设$H_2(j\omega )$是一个全通系统， 所以我们只需要一个等于1的幅度，所以输出$x_2(t)$只是输入$x_1(t)$的延时，$x_1(t)$被群延时。（这里之所以用连续时间而不是离散时间来描述这幅图，是因为这样可以暂时避免这样的问题：如果这个斜率是非整数，它的延迟的问题。）
一个窄带信号$x[n]=s[n]cos({\omega }_{0}n+\theta )$，此处先忽略相位因子$\theta$，有$$x[n]=s[n]cos{\omega }_{0}n=s[n]\frac{1}{2}(e^{j{\omega }_{0}n}+e^{-j{\omega }_{0}n})$$第一个系统$H_1(j\omega )$在做什么呢？将$e^{-j{\varphi }_0}$与$s[n]\frac{1}{2}{e}^{j{\omega }_{0}n}$相乘，将$e^{j{\varphi }_0}$与$s[n]\frac{1}{2}{e}^{-j{\omega }_{0}n}$相乘，因此有
$$\begin{gathered} y[n]=s[n]\frac{1}{2}(e^{-j{\varphi }_0}{e}^{j{\omega }_{0}n}+e^{j{\varphi }_0}{e}^{-j{\omega }_{0}n}) \\ =s[n]cos({\omega }_{0}n-{\varphi }_0) \\ =s[n]cos[{\omega }_0(n-\frac{{\varphi }_0}{{\omega }_0})] \end{gathered}$$这样写的话，可以把它解释为一个延迟。而这种延迟最终被称为相位延迟，所以是与相位相关的延迟。
（这里请允许我使用引号，这样我们就不必钻研群延迟不是整数时的含义了。）所以结果是简单地以群延迟来延迟$x_1[n]$，所以这只是用n减去群延迟来代替n。最终效果是常数偏移加上斜率的组合。
结果是对于窄带信号有两个影响。一个影响是对信号的包络：$$s[n-{\tau }_g({\omega }_0)]$$包络被群延迟延时；
另一个影响是对信号的相位：$$n-{\tau }_g({\omega }_0)-\frac{{\varphi }_0}{{\omega }_0}$$被定义为相位延迟。

现有一个宽带信号，我可以把它看作是窄带信号的线性组合。这里可以想象把我的信号放到一个带通滤波器组里，假设是一个可完美重构的滤波器组，换句话说，把所有这些输出加起来，这将是等于原始输入。这里只是把信号拆烂成了多个非常窄的窄带部分，任何一个宽带信号都是窄带信号的叠加。下面宽带信号的傅里叶变换中，有$X(e^{j\omega })={\sum }_m{X}_m(e^{j\omega })$

把一个宽带信号通过一个系统，有非线性相位（非恒定群延迟），这些窄带频率组的每一个将经历：包络将经历一个不同的延迟，即$s_m[n-{\tau }_g({\omega }_m)]$，载波也会经历不同的延迟（相位延迟），即$(n-{\tau }_p)$。
如果我把一个脉冲放入系统中，经过傅立叶变换器，在所有频率下都是一个常数。但是，如果我把恒定的频率内容分解成小的窄带部分，或者小的窄带频率组， 每一个频率组它的包络会经过不同的延迟。
所以这里是我的滤波器的群延迟，它表明上面这些频率附近的频率基本上不会有任何延迟。

而这个频率组和这个频率组相比，和这个频率组相比，这个频率组要经过一个相当大的延时。所以我希望在脉冲响应中看到的是，高频首先出现。然后看到延迟后的一个频率组出现，再看到延迟后的一个频率组出现。这里说的是一个全通系统，你会认为，一个全通系统， 如果一个脉冲进去， 脉冲要出来，全通系统通过一切，问题是全通系统能以相同的振幅通过所有的频率，它不会以相同的相位通过所有的频率。所以你得到的是这种效果，从一个脉冲开始，所有的频率组都相加。你把脉冲通过一个非线性相位的全通信道，然后发生的事情是，脉冲响应在时间上被分散了，不同的频率在不同的时间出来。
举例来说，如果你把语音通过一个全通系统播放，而这个全通系统有很多的色散，就很难理解所讲的内容，即使傅里叶变换的幅度没有受到任何影响。

T1.3 清单

• 非线性相位对于窄带信号的影响可以通过窄带信号中心频率（载波）周围的相位的泰勒级数展开来解释。
• 对于窄带信号，相位的影响是通过群延迟来延迟包络，通过相位延迟来延迟载波。
• 对于宽频带信号，群延迟的作用是通过群延迟来延迟每个频率 “群”。因此，在不同频率上不是常数的群延迟会导致色散。