2019 高教社杯数模竞赛A题 高压油管的压力控制 题解

初见这道题目的时候真是一头雾水。由于和队友们都没有建模的经历，初次作业就碰上了于这种硬核的物理题，属实劝退（

本文是从最终的latex论文摘要出来的，公式因为katex不完全兼容的问题没有显示序号QAQ

问题一题解

分析

要使高压油管内的燃油压力稳定在给定值100MPa，我们的切入点应该是将压力转换成可直接计算的量。附录三中已经给出了已知燃油的压力与弹性模量的关系，我们又已知燃油的压力变化量与密度变化量满足一微分方程，根据这两个条件我们可以得到燃油压力与密度的关系。再根据进出口的流量函数，我们可以推出计算出油管内燃油密度的变化规律。到此，我们就可以将原问题转化为对燃油密度优化的问题了。

（关于求解微分方程这一步骤，我觉得直接近似求解和拟合都可以，但是拟合的话最好不要用线性，二次和指数的效果相对可能好一丢丢。）

问题一的第二小问，可以在第一小问的工作上求解。第一小问是优化因变量压力，第二小问则是优化自变量时间，我们需要系统达到稳定的时间精确控制在指定数值左右。

求解

求解微分方程

因为燃油的压力变化量与密度变化量成正比，易知微分方程：

$$\frac{dP}{d\rho }=\frac{E}{\rho }$$

即$$\frac{dP}{E}=\int \frac{d\rho }{\rho }+C$$

由附录三知$$E=0.029P^2+3.08P+1571.6$$

根据已知条件当压力为100 MPa时，燃油的密度为$0.850mg/m{m}^3$解得$$P=\frac{\rho -0.80853816}{0.001859637768-0.00170\rho }\times 10^{-3}$$
$$\rho =0.80853816+0.80853816\frac{0.0006P}{1+0.0017P};$$

求解管内燃油密度变化

根据流量计算公式$$Q=CA\sqrt{\frac{2\Delta P}{\rho }}$$

可以得到燃油进出速度$$v(t)=CA\sqrt{\frac{2\Delta P}{\rho }}$$

燃油进入时的速度(一个周期内)
$$I(t)=\{\begin{array}{ll}CA\sqrt{\frac{2[P_1(t)-P_2(t)}{{\rho }_1}}& ,t\in \left(0,t_1\right)\\ 0& ,t\in \left(t_1,T_1\right)\end{array}$$
燃油喷出时的速度(一个周期内)
$$O(t)=\{\begin{array}{ll}100t& ,t\in \left(0,0.2\right)\\ 20& ,t\in \left(0.2,2.2\right)\\ -100t+240& ,t\in \left(2.2,2.4\right)\\ 0& ,t\in (2.4,T_2)\end{array}$$

油管增加的质量
$$m_1(t)={\rho }_{1}I(t)\Delta t$$

油管减少的质量
$$m_2(t)={\rho }_{2}O(t)\Delta t$$

油管内质量的变化
$$m_1(t)-m_2(t)={\rho }_{1}I(t)\Delta t-{\rho }_{2}O(t)\Delta t$$

油管内密度的变化
$${\rho }_2(t+\Delta t)-{\rho }_2(t)=\frac{1}{V}\left[{\rho }_{1}I(t)-{\rho }_{2}O(t)\right]\Delta t$$
所以给定单向阀开启时长的值，我们就能通过燃油进出流量的函数来求得油管内质量的变化，进而求得密度的变化。再根据密度与压力的关系函数，我们就能求得压力的变化。当我们取很小的时间间隔为步长时，压力可以取离散值，那么原问题可以看作优化
$$min\frac{{\sum }_{i=1}^N\left|P\left(t_k\right)-P_0\right|}{N}$$

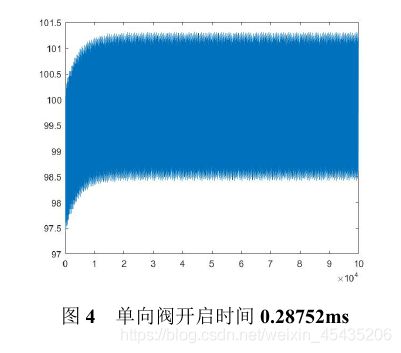
因为单向阀每次开启结束后需要关闭10ms，考虑到周期的数量级，我们先将最优解的查找范围限定在(0.10ms)之间，步长为0.5ms。取100s中后5s压力稳定值的平均值作为结果，画出图像如图1所示。

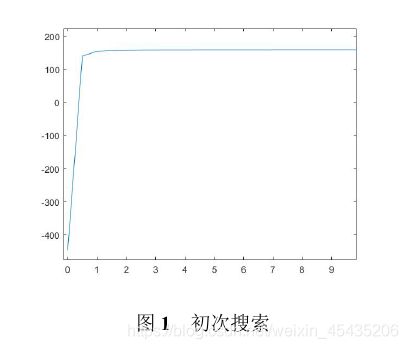
由图1可以看出压力稳定在100Mpa时时间区间应该是(0.27ms,0.29ms)，我们在此区间再次搜索最优解。步长为0.01ms。结果如图2所示。

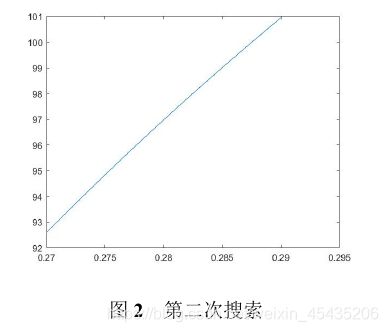
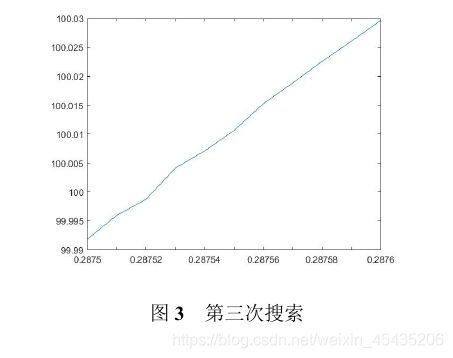
由图2可以进一步缩小区间至(0.2875ms,0.2876ms)，我们在此区间再次搜索最优解。步长为0.00001ms。结果如图3所示。

得到最后结果0.28752ms。对应压力变化图如图4所示。

问题二题解

分析

问题二与问题一一样都是压力控制，不同的是我们需要从几何图形上入手。进油时，在柱塞的压油过程中，柱塞被凸轮驱动上下运动，从而改变柱塞腔内的压力，决定高压油泵内的燃油是否进入。那么，由凸轮边缘曲线与角度的关系可以求得柱塞的运动情况，从而得到腔内的体积变化情况，进而求得腔内燃油的密度变化，由燃油压力与密度关系式得到其压力变化。喷油时，由已知喷油器的喷嘴结构及其工作条件和附录可以得到针阀与密封座之间的空隙面积。将问题一中给定的喷油器工作次数、高压油管尺寸和初始压力等条件代入模型求解，搜索凸轮的角速度，使高压油管内的压力尽量稳定在100 MPa左右。

求解

燃油的进入

由附件1给出的凸轮轮廓线极径、极角的关系，用插值法处理数据，经过三次差值后得到拟合轮廓线。对于凸轮的运动规律，可由对拟合曲线进行反解得到。在柱塞的运动过程中，我们关注其升程的最大值和最小值。其对应于凸轮轮廓线变化过程中的最高点与最低点。通过观察凸轮轮廓线发现，两个最值对应于凸轮轮廓线上的两端圆弧。以水平和竖直方向建立直角坐标系，将柱塞与轮廓接触点标为M，则该点对应坐标由式(18)计算
$$\{\begin{array}{l}x=r\cdot \cos \theta \\ y=r\cdot \sin \theta \end{array}$$
图8为凸轮与柱塞连接驱动的几何示意图，M点为某时刻凸轮轮廓线上y坐标值最大的点。

初始位置时极角${\varphi }_0=0$。当凸轮运动到最大值点时，低压燃油将会在油泵作用下充满柱塞腔。设凸轮轮廓线上的点横坐标为$X_0=\left[x_{1,0},x_{2,0},\dots ,x_{m,0},\dots ,x_{n,0}\right]$,相应的纵坐标为$Y_0=\left[y_{1,0},y_{2,0},\dots ,y_{m,0},\dots ,y_{n,0}\right]$

为了求任意时刻对应的x，y坐标值，设凸轮转动角度${\varphi }_k$，由上文坐标的计算公式可得，转角为${\varphi }_k$时的坐标为：

$$\{\begin{array}{l}{x}_{m,k}=x_{m,0}\cdot \cos {\phi }_k-y_{m,0}\cdot \sin {\phi }_k\\ y_{m,k}=x_{m,0}\cdot \sin {\phi }_k-y_{m,0}\cdot \cos {\phi }_k\end{array}$$

由此可得当凸轮转角为${\varphi }_k$时，凸轮轮廓线的横坐标为$X_k=\left[x_{1,k},x_{2,k},\dots ,x_{m,k},\dots ,x_{n,k}\right]$对应的纵坐标为$Y_k=\left[y_{1,k},y_{2,k},\dots ,y_{m,k},\dots ,y_{n,k}\right]$

若凸轮结构中的基圆半径为$R_0$，则当凸轮转角为${\varphi }_k$时，柱塞的升程$s_k$为$s_k=\max \left(Y_k\right)-R_0$,由求得的升程，根据$V=\left(h_2-s_k\right)S$可得该时刻高压油泵内的燃油体积。上式中S为柱塞腔的底面积，$h_2$为柱塞运动到下止点时，柱塞底端与高压油泵顶端的距离。根据问题2中题设中的信息，柱塞运动到下止点时，低压燃油的压力为0.5MPa，根据燃油压力与密度对应关系的表达式，即可得到高压油泵内低压燃油的密度${\rho }_0$。

凸轮运动到下止点，柱塞腔内燃油体积为$V_0=S{h}_2$，则腔内的燃油质量为$m={\rho }_0{V}_0$。凸轮转角为${\varphi }_k$时，腔内燃油质量不变，体积因柱塞的升降变为$V_1$，当没有再次进油时，腔内燃油密度为${\rho }_1=\frac{m}{V_1}=\frac{{\rho }_0{h}_2}{h_2-s_k}$

现考虑凸轮转速与转角间关系。设凸轮转动角速度为$\omega$，则在$\Delta t$时间内凸轮转过角度为${\varphi }_{k+1}-{\varphi }_k=\omega \Delta t$

设凸轮转角为${\varphi }_k$时腔内压力为$P_1(t)$,根据问题2题设，高压油管内的压力$P_2(t)$若小于腔内压力，则高压油泵开始往油管内进油，进油量为$I(t)=CA\sqrt{\frac{2\left[P_1(t)-P_2(t)\right]}{{\rho }_1}}$

燃油的喷出

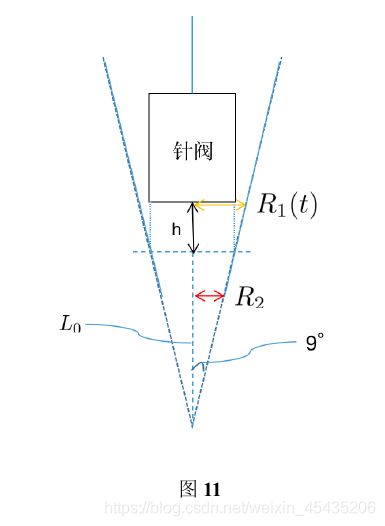
对喷油器喷嘴的示意图分析，将针阀与密封座之间的空隙面积记为S1，密封座底部面积记为S2。图9、图10分别为喷油嘴的的纵向截面和横向截面的各部分面积示意图。

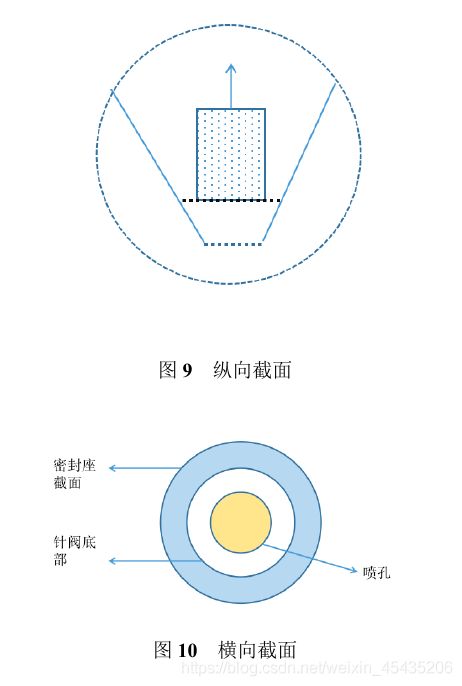
根据附件2提供的针阀升程和时间的关系可以发现，针阀升程在[0,0.45]区间递增，在[0.45,2]区间稳定在2mm，在[2,2.46]区间内递减到0，在接下来的时间内恒为0。令针阀在某时刻的升程为$h(t)$，密封座的截面半径为$R_1(t)$，喷孔半径$R_2=0.7mm$，由下图的几何关系图，底座圆锥半角为9度，将喷孔与圆锥订点的距离记为$L_0$。其几何关系如图11所示。

根据上图的几何关系，密封座截面半径为：$$R_1(t)=\left[h(t)+L_0\right]\tan 9$$

对应的针阀与密封座之间的面积S1为：$$S_1(t)=\pi {\left[h(t)+L_0\right]}^2{\tan }^{2}9$$

喷孔面积$s_2$为 $\pi R_2^2$，故燃油喷出时，喷出燃油的流经面积$S(t)$，则$$S(t)=\min \left\{S_1(t),S_2\right\}$$

假设喷油嘴外部压强等于一标准大气压$P_N$，高压油管内压力为$P_2(t)$，则由高压油管的流量计算公式，可得燃油喷出的流量$O(t)$为$$O(t)=CS(t)\sqrt{\frac{2\left[P_2(t)-P_N\right]}{{\rho }_2}}$$

同理问题一，当我们取很小的时间间隔为步长时，压力可以取离散值，那么原问题可以看作优化
$$min\frac{{\sum }_{i=1}^N\left|P\left(t_k\right)-P_0\right|}{N}$$

求解该问题得到凸轮的角速度。

模型的求解

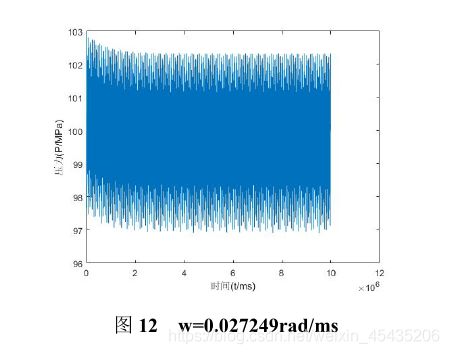
以0.01为步长搜索凸轮运动角速度，反复尝试使管内压力波动尽可能小。求得凸轮角速度为0.027249rad/ms时，高压油管压力稳定在100MPa左右。压力时间曲线如图12所示。

问题三题解

分析

问题三在问题二的基础上增加了一个喷油嘴，除此之外均与问题二相同，增加喷油嘴可以更快地将供油排出，从而减少高压油管内压力变化峰值，使油管内压力更加稳定。因为两个喷油嘴的喷油规律相同，所以我们可以直接在问题二基础上进行下一步工作。在原有模型的基础上考虑单向减压阀的引入。由单向减压阀的工作原理，设置单向减压阀的开启条件，设置阈值压强,管内压强大于阈值压强为减压阀开启条件，即此时燃油从油管内回流进减压阀，由流量计算公式求解减压阀中回流的燃油流量，从而得到高压油管内的燃油密度，进而得其压力，得到压力波动最小时的最优解。

求解

若要使高压油管内的压力稳定在100MPa左右，需调整喷油和供油策略。通过改变凸轮转速可以调整燃油的进入，通过单向减压阀调整高压油管内的压力；通过控制两个喷油嘴的喷油时间和调整针阀下止点来改变喷油策略。

要寻求合适的供油策略，相当于寻找一个合适的凸轮转动角速度$\omega$，在该部分的求解中，我们将$\omega$的值与其他参量联合起来进行求解。

喷油策略调整的主要目标为调节两个喷油嘴的喷油时间。这里假设每个喷油嘴的喷油规律与问题2中的相同，即1s喷射10次。由于两喷油嘴喷油存在时间间隔，故设两喷油嘴喷油时间间隔为$\Delta t$，喷油嘴1在t=0时刻开始喷射，喷油嘴2在$t=\Delta t$时刻开始喷射。

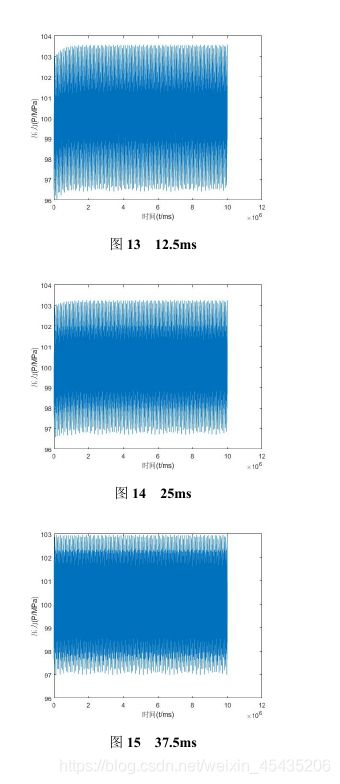
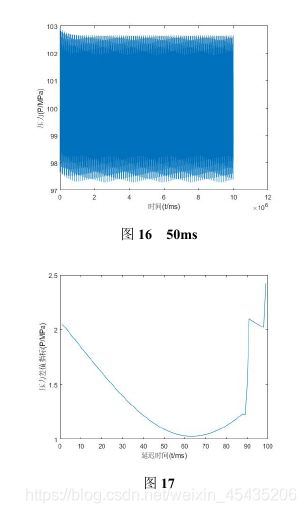
搜索两个喷油嘴的喷油间隙。当喷油嘴开始喷射时间间隔在0-50ms内变化时，取特征点12.5ms，25ms 37.5ms，50.0ms。其压力变化如图13-16所示。

由图可得，当喷油嘴开始喷射时间间隔在0-50ms内变化时，管内压力在稳定值附近的波动幅度逐渐减小借由前面的分析，可知道0-50ms时间间隔的大致趋势，我们画出0-100ms时压强差指标的图。如图17所示。

从图中可以看到，延迟时间在63ms附近压力差最小。

在上述调整策略的基础上引入单向减压阀，当高压油管内压力过高时降低压力。使用单向减压阀时，需设置一个压力阈值$P^{\prime }$，当管内压力大于阈值时开启减压阀，使得管内燃油回流至外部低压油路，从而减小管内压力。设回流的燃油流量为$Q_d$，单向减压阀单次开启时长为$t_d$，则
$$Q_d=CA\sqrt{\frac{2[P(t)-P_e(t)]}{\rho }}$$

当油管内压力小于阈值P’时，单向减压阀关闭。因此需求凸轮旋转角速度$\omega$和压力阈值$P^{\prime }$，最小化压力变化，即 $$min{P}_{max}-P_{min}$$

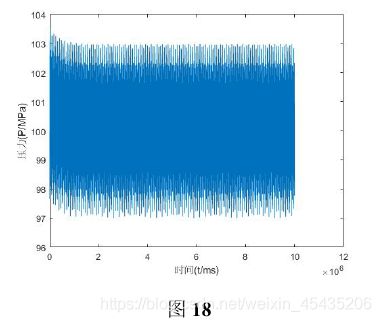
最终找到的最优解为角速度0.0545，$\Delta t=63ms$,对应压力变化如图18：

代码附录

Q1.1

%密度函数，压力函数，出油函数
P=@(x)(x-0.80853816)/(0.001859637768-0.00170*x);
density=@(x)0.80853816*(1+ (0.6*10^-3*x)/(1+0.0017*x));
O=@(x)100*x.*(x<=0.2)+20.*(x>0.2&x<=2.2)-(100*x-240).*(x>2.2&x<=2.4)+0.*(x>2.4);

%规定常量
delta_t=0.01;
C=0.85;
V=(5^2)*500*pi;
A=(1.4/2)^2*pi;
p0=100;        
m0=density(100)*V; 
ml=m0;

y_test=[]
x_test=[]
l=0;

for t=0.28752:0.28752

result=0;
t_out=0;t_in=0;flag=0;
x=[];y=[];   %画图坐标
l=l+1;

for i=0:delta_t:100000   


flag=flag+1;
x(flag)=i;
y(flag)=p0;


vin=0;
if t_in>t+10
t_in=t_in-(t+10);
end
if t_in<t
vin=(C*A*(2*(160-p0)/0.8696)^(.5));
end

t_in=t_in+delta_t;
m_in=0.8696*vin*delta_t; 
if t_out>100
t_out=t_out-100;
end

vout=O(t_out)*delta_t;
t_out=t_out+delta_t;
mout=vout*density(p0) ;
delta_m=m_in-mout;

rho_now=(m0+delta_m)/V;
p0=P(rho_now);

m0=m0+delta_m;

flag=flag+1;
x(flag)=i;
y(flag)=p0;
end 

%搜索判定条件
y_ave=0;k=0;
for j=9950000:10000000
k=k+1;
y_ave=y_ave+y(j);
end
y_ave=y_ave/k;
y_test(l)=y_ave;
x_test(l)=t;
end

plot(x,y)
%plot(x_test,y_test);

Q1.2

%密度函数，压力函数，出油函数
P=@(x)(x-0.80853816)/(0.001859637768-0.00170*x);
density=@(x)0.80853816*(1+ (0.6*10^-3*x)/(1+0.0017*x));
O=@(x)100*x.*(x<=0.2)+20.*(x>0.2&x<=2.2)-(100*x-240).*(x>2.2&x<=2.4)+0.*(x>2.4);

%规定常量
delta_t=0.01;
C=0.85;
V=(5^2)*500*pi;
A=(1.4/2)^2*pi;
p0=100;        
m0=density(100)*V; 
ml=m0;

y_test=[]
x_test=[]
l=0;
t=0;


result=0;
t_out=0;t_in=0;flag=0;
x=[];y=[];   %画图坐标
l=l+1;

for i=0:delta_t:20000   


flag=flag+1;
x(flag)=i;
y(flag)=p0;

%if i<5000
%   t=0.0001*i+0.26485;  
%end
%if i>=5000
%   t=0.76485;  
%end
%if i<2000
%   t=-0.0001*i+0.96685;  
%end
%if i>=2000
%   t=0.76485;  
%end
if i<10000
t=0.00004*i+0.36485;  
end
if i>=10000
t=0.76485;  
end

vin=0;
if t_in>t+10
t_in=t_in-(t+10);
end
if t_in<t
vin=(C*A*(2*(160-p0)/0.8696)^(.5));
end

t_in=t_in+delta_t;
m_in=0.8696*vin*delta_t; 
if t_out>100
t_out=t_out-100;
end

vout=O(t_out)*delta_t;
t_out=t_out+delta_t;
mout=vout*density(p0) ;
delta_m=m_in-mout;

rho_now=(m0+delta_m)/V;
p0=P(rho_now);

m0=m0+delta_m;

flag=flag+1;
x(flag)=i;
y(flag)=p0;
end 

%搜索判定条件
%y_ave=0;k=0;
%for j=9950000:10000000
%    k=k+1;
%    y_ave=y_ave+y(j);
%end
%y_ave=y_ave/k;
%y_test(l)=y_ave;
%x_test(l)=t;


plot(x,y)
%plot(x_test,y_test);

Q2

 %密度函数，压力函数
 density=@(x)0.80853816*(1+ (0.6*10^-3*x)/(1+1.7*10^-3*x));
 P=@(x)-(90071992547409920000*x-72826643121816530000)/(153122387330596864*x-167501279180178019);
 
 c=0.85;
 V=(5^2)*500*pi;
 A=(1.4/2)^2*pi;
 A_oil=(5/2)^2*pi;
 H=5.8446;
 Vmax=H*A_oil;
 M=Vmax*density(0.5);
 m0=density(100)*V; 
 delta_t=0.01;
 p_wai=0.1;
 theta=xlsread('附件1-凸轮边缘曲线','sheet1','A2:A629');
 r=xlsread('附件1-凸轮边缘曲线','sheet1','B2:B629');
 L0=0.7/tan(9/180*pi)*2.5/1.4;
 A_zhen=(2.5/2)^2*pi;
 A_kong=0.7^2*pi;
 k=[];x=[];y=[];
 al=xlsread('附件2-针阀运动曲线','sheet1','B2:B46');
 bl=2*ones(156,1);
 cl=xlsread('附件2-针阀运动曲线','sheet1','E2:E46');
 h_zhen=[al;bl;cl;zeros(9755,1)]';
 
 
 for i=1:628
 x(i)=sin(theta(i))*r(i);
 y(i)=cos(theta(i))*r(i);
 end
 s=[];u=1;
 
 for i=0:0.01:6.27
 xk=[];
 yk=[];
 for j=1:628
 xk(j)=x(j)*cos(i)-y(j)*sin(i);
 yk(j)=x(j)*sin(i)-y(j)*cos(i);
 end
 s(u)=max(yk)-2.4130;
 u=u+1;
 end
 
 s=interp1([0:0.01:6.27],s,[0:0.000001:6.27],'spline');
 w=0.027249;
 j=1;
 u=1;
 p0=100; 
 rho0=0.85;
 m_oil=M;
 fy=1;
 
 for i=0:delta_t:100000
 fy=fy+int32(w*delta_t/0.000001);
 while fy>6270001
 fy=fy-6270001;
 m_oil=M;
 end
 h_now=H-s(fy);
 V_now=A_oil*h_now;
 rho_now=m_oil/V_now;
 P_now=P(rho_now);
 vin=0;
 if P_now>p0
 vin=c*A*(2*(P_now-p0)/rho_now)^(.5);
 end
 m_in=rho_now*vin*delta_t;
 m_oil=m_oil-m_in;
 rl=(h_zhen(u)+L0)*tan(9/180*pi);h_z=h_zhen(u);
 A_out=pi*rl^2-A_zhen;
 if pi*rl^2-A_zhen-A_kong>0
 A_out=A_kong;
 end
 if h_zhen(u)==0
 A_out=0;
 end
 u=u+1;
 if u>10001
 u=u-10001;
 end
 vout=c*A_out*(2*(p0-p_wai)/rho0)^(.5);
 mout=vout*rho0*delta_t;
 delta_m=m_in-mout;
 rho0=(m0+delta_m)/V;
 k(j)=p0;
 p0=P(rho0);
 j=j+1;
 
 m0=m0+delta_m;
 end
 
 
 plot(k)
 xlabel('时间(t/ms)')
 ylabel('压力(P/MPa)')

Q3

%密度函数，压力函数
 density=@(x)0.80853816*(1+ (0.6*10^-3*x)/(1+1.7*10^-3*x));
 P=@(x)-(90071992547409920000*x-72826643121816530000)/(153122387330596864*x-167501279180178019);
 
 
 c=0.85;
 V=(5^2)*500*pi;
 A=(1.4/2)^2*pi;
 A_oil=(5/2)^2*pi;
 H=5.8446;
 Vmax=H*A_oil;
 M=Vmax*density(0.5);
 m0=density(100)*V; 
 delta_t=0.01;
 p_wai=0.1;
 theta=xlsread('附件1-凸轮边缘曲线','sheet1','A2:A629');
 r=xlsread('附件1-凸轮边缘曲线','sheet1','B2:B629');
 L0=0.7/tan(9/180*pi)*2.5/1.4;
 A_zhen=(2.5/2)^2*pi;
 A_kong=0.7^2*pi;
 k=[];x=[];y=[];
 al=xlsread('附件2-针阀运动曲线','sheet1','B2:B46');
 bl=2*ones(156,1);
 cl=xlsread('附件2-针阀运动曲线','sheet1','E2:E46');
 h_zhen=[al;bl;cl;zeros(9755,1)]';
 yanchi=5000;
 for i=10001:-1:yanchi+1
 h_zhenl(i)=h_zhen(i-yanchi);
 end
 for i=1:1:yanchi
 h_zhenl(i)=0;
 end
 
 for i=1:628
 x(i)=sin(theta(i))*r(i);
 y(i)=cos(theta(i))*r(i);
 end
 s=[];u=1;
 
 for i=0:0.01:6.27
 xk=[];
 yk=[];
 for j=1:628
 xk(j)=x(j)*cos(i)-y(j)*sin(i);
 yk(j)=x(j)*sin(i)-y(j)*cos(i);
 end
 s(u)=max(yk)-2.4130;
 u=u+1;
 end
 
 s=interp1([0:0.01:6.27],s,[0:0.000001:6.27],'spline');
 w=0.0545;
 j=1;
 u=1;
 p0=100; 
 rho0=0.85;
 m_oil=M;
 fy=1;
 
 for i=0:delta_t:100000
 fy=fy+int32(w*delta_t/0.000001);
 while fy>6270001
 fy=fy-6270001;
 m_oil=M;
 end
 h_now=H-s(fy);
 V_now=A_oil*h_now;
 rho_now=m_oil/V_now;
 P_now=P(rho_now);
 vin=0;
 if P_now>p0
 vin=c*A*(2*(P_now-p0)/rho_now)^(.5);
 end
 m_in=rho_now*vin*delta_t;
 m_oil=m_oil-m_in;
 rl=(h_zhen(u)+L0)*tan(9/180*pi);
 rl2=(h_zhenl(u)+L0)*tan(9/180*pi);
 
 A_out=pi*rl^2-A_zhen;
 if pi*rl^2-A_zhen-A_kong>0
 A_out=A_kong;
 end
 if h_zhen(u)==0
 A_out=0;
 end
 
 Al_out=pi*rl2^2-A_zhen;
 if pi*rl2^2-A_zhen-A_kong>0
 Al_out=A_kong;
 end
 if h_zhenl(u)==0
 Al_out=0;
 end
 u=u+1;
 if u>10001
 u=u-10001;
 end
 vout=c*(A_out+Al_out)*(2*(p0-p_wai)/rho0)^(.5);
 mout=vout*rho0*delta_t;
 delta_m=m_in-mout;
 rho0=(m0+delta_m)/V;
 k(j)=p0;
 p0=P(rho0);
 j=j+1;
 
 m0=m0+delta_m;
 end
 
 
 
 plot(k)
 xlabel('时间(t/ms)')
 ylabel('压力(P/MPa)')