Leetcode 889. 根据前序和后序遍历构造二叉树-105. 从前序与中序遍历序列构造二叉树-106. 从中序与后序遍历序列构造二叉树

题目

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7
后序遍历 postorder = [9,15,7,20,3]

解题思路

中序可以和前序、后序、层序的任意一个搭配来构建唯一的二叉树。
若没有中序，其他的序列搭配都无法构建唯一的二叉树，因为先序、后序、层序都用于提供根结点，只有中序才能区分左右子树。

根据中序、后序构造树

class Solution {
     
    private int[] post; //后序序列
    private Map<Integer, Integer> map; //哈希表记录结点值在中序里的下标

    public TreeNode buildTree(int[] inorder, int[] postorder) {
     
        post = postorder;
        map = new HashMap<>();
        for(int i = 0; i < inorder.length; i++)
            map.put(inorder[i], i);
        return helper(0, inorder.length - 1, post.length - 1);
    }

    /**
     * 根据中序始末下标构建树
     * @param begin 中序的起始下标
     * @param end 中序的结束下标
     * @param postidx 根结点在后序里的下标
     * @return 返回树的根结点
     */
    private TreeNode helper(int begin, int end, int postidx) {
     
        if(begin > end)    return null; //没有结点，返回空树
        int rootidx = map.get(post[postidx]); //根结点在中序里的下标，用于区分左右子树
        TreeNode root = new TreeNode(post[postidx]);
        int rightcnt = end - rootidx; //右子树结点数
        root.left = helper(begin, rootidx - 1, postidx - rightcnt - 1); //根据子树的中序构建子树
        root.right = helper(rootidx + 1, end, postidx - 1);
        return root;
    }
}

根据中序、前序构造树

class Solution {
     
    private int[] pre; //前序
    private Map<Integer, Integer> map; //哈希表用于记录结点值在中序里的下标

    public TreeNode buildTree(int[] preorder, int[] inorder) {
     
        pre = preorder;
        map = new HashMap<>();
        for(int i = 0; i < inorder.length; i++)
            map.put(inorder[i], i);
        return helper(0, inorder.length - 1, 0);
    }

    /**
     * 根据中序始末下标构建树
     * @param begin 中序起始下标
     * @param end 中序结束下标
     * @param preidx 根结点在前序里的下标
     * @return 返回树的根结点
     */
    private TreeNode helper(int begin, int end, int preidx) {
     
        if(begin > end)    return null; //没有结点，返回空树
        int rootidx = map.get(pre[preidx]); //根据根结点在前序里的下标求出根节点值后查询其在中序里的下标，用于区分左右子树
        TreeNode root = new TreeNode(pre[preidx]);
        root.left = helper(begin, rootidx - 1, preidx + 1); //根据子树中序构建子树
        int leftcnt = rootidx - begin; //左子树结点数
        root.right = helper(rootidx + 1, end, preidx + leftcnt + 1);
        return root;
    }
}

前序，后序构造树

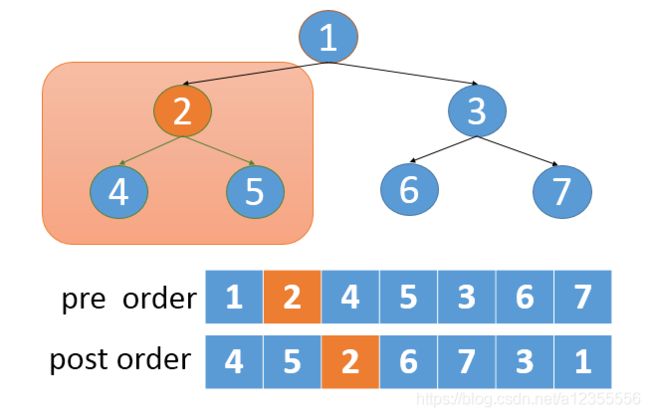
如果遍历这个左子树
前序遍历的结果是[2,4,5]
后序遍历的结果是[4,5,2]

我们根据2就可以确定出后序遍历的左子树范围
因为后序遍历的整棵树的结果是[4,5,2,6,7,3,1]
现在我们找到2了，根节点的位置是固定出现在最后的，那么右子树的范围也就可以确定了。
后序遍历数组下标是从0开始的，我们确定了2的位置，还需要+1，这样就得到了整个左子树的个数。

class Solution {
     
    private int[] pre; //前序
    private Map<Integer, Integer> map; //记录结点值在后序中的下标
    public TreeNode constructFromPrePost(int[] pre, int[] post) {
     
        this.pre = pre;
        map = new HashMap<>();
        for(int i = 0; i < post.length; i++)
            map.put(post[i], i);
        return build(0, pre.length - 1, 0);
    }
    /**
     * 根据前序后序构建树
     * @param begin 前序的起点下标
     * @param end 前序的终点下标
     * @param postBegin 后序的起点下标
     * @return 返回构建的树
     */
    private TreeNode build(int begin, int end, int postBegin) {
     
        if(begin > end)    return null; //没有结点，返回空树
        TreeNode root = new TreeNode(pre[begin]); //前序第一个结点就是当前根结点
        if(begin < end) {
      //若还有子结点
            int leftv = pre[begin + 1]; //默认一定有左子树，左子树根结点下标即begin + 1
            int leftcnt = map.get(leftv) - postBegin + 1; //计算左子树结点数
            root.left = build(begin + 1, begin + leftcnt, postBegin); //递归构建子树
            root.right = build(begin + leftcnt + 1, end, postBegin + leftcnt);
        }
        return root;
    }
}

中序存在与否对树的构建有什么影响

建议先完全掌握这篇题解中的两段代码。
中序+前序/后序

关键在于理解：前序和后序都只用于提供根结点，只有中序才能区分左右子树。
因为有了中序序列，得到根结点在中序中的位置后，根结点左边的一定都是左子树结点，右边的一定都是右子树结点，这是由中序定义的左->中->右遍历顺序决定好了的。
所以我们可以严格区分出左右子树，递归地构建出唯一的二叉树。

值得注意的是，本题的前序+后序是不能构建唯一的二叉树的。

或许会有人说，前序+后序似乎也能构建唯一的二叉树。
其实不能，那么本题中的什么东西使人产生这种错觉呢。
考虑下面代码中的这一段：

int leftv = pre[begin + 1]; //默认一定有左子树，左子树根结点下标即begin + 1
int leftcnt = map.get(leftv) - postBegin + 1; //计算左子树结点数
root.left = build(begin + 1, begin + leftcnt, postBegin); //递归构建子树
root.right = build(begin + leftcnt + 1, end, postBegin + leftcnt);

一上来就求左子树根结点的值leftv，和左子树结点数leftcnt，但是并不考虑是否存在左子树。这样的做法认为只要有子结点，就默认有左子树，没有考虑到可能压根就不存在左子树，可能仅仅只有右子树。因此，前序+后序是不能构建出唯一的二叉树的。

参考：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/marvelzhong-deng-de-xue-xi-bi-ji-106-by-tyanyone-2/