1631 最小体力消耗路径
题目描述:
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
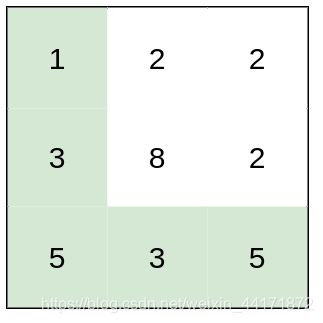
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路劲差值最大值为 3 。
示例 2:
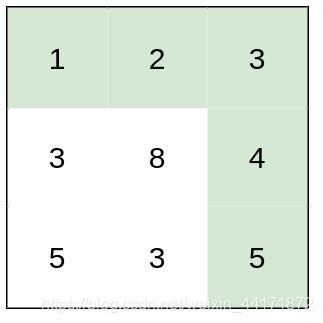
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
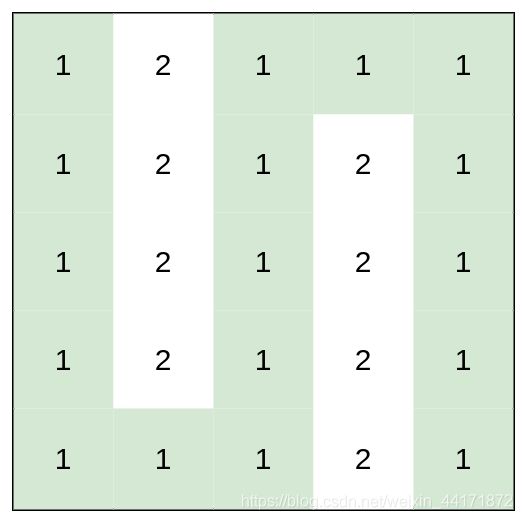
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
方法1:
主要思路:
(1)二分查找+dfs;
(2)将可能的体力值的范围作为二分查找的范围,找出其中的中间值,作为当前判断从左上角到右下角的可行路径的标准值;
(3)若在当前的中间值下,不存在可能的路径,则说明需要更大的中间值,故调整左边界, 既left=mid+1,若能到达右下角,则说明可能存在更小的值,则更新右边界, 既right=mid;
class Solution {
public:
const int step[4][2]={
{
1,0},{
-1,0},{
0,1},{
0,-1}};//每次前进的步骤
int minimumEffortPath(vector<vector<int>>& heights) {
//确定的初始的二分范围
int left=0;
int right=999999;
while(left<right){
//二分搜索
//标识访问过的路径
vector<vector<bool>> sign(heights.size(),vector<bool>(heights[0].size(),false));
//当前的体力中间值
int mid=left+(right-left)/2;
if(dfs(heights,sign,mid,0,0)){
//深度搜索,判断当前中间值下,是否可能到达右下角
right=mid;
}
else{
left=mid+1;
}
}
//返回
return left;
}
//深度搜索
bool dfs(vector<vector<int>>& heights,vector<vector<bool>>& sign,int& mid,int x,int y){
if(x==sign.size()-1&&y==sign[0].size()-1){
//说明到达了右下角,直接返回true
return true;
}
sign[x][y]=true;//标识当前访问过的路径
//可能前进的方向
for(int i=0;i<4;++i){
//当期可能踏出的下一步
int cur_x=x+step[i][0];
int cur_y=y+step[i][1];
//前四个条件满足该位置有效,第五个条件保证当前点之前没有访问过,第六个条件保证两点之间满足体力值要求
if(cur_x>=0&&cur_x<sign.size()&&cur_y>=0&&cur_y<sign[0].size()&&!sign[cur_x][cur_y]&&(abs(heights[x][y]-heights[cur_x][cur_y])<=mid)){
if(dfs(heights,sign,mid,cur_x,cur_y)){
//在新的位置进行深度搜索
return true;
}
}
}
return false;//跳出循环,说明不能到达右下角
}
};
方法2:
主要思路:
(1)二分查找+bfs;
(2)和方法1的主要差异点是将深度搜索变换成了广度搜索;
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
//确定的初始的二分范围
int left=0;
int right=999999;
const int step[4][2]={
{
1,0},{
-1,0},{
0,1},{
0,-1}};//每次前进的步骤
while(left<right){
//二分搜索
queue<pair<int,int>> q;//存储广度路径
q.push({
0,0});
//标识访问过的路径
vector<vector<bool>> sign(heights.size(),vector<bool>(heights[0].size(),false));
sign[0][0]=true;
//当前的体力中间值
int mid=left+(right-left)/2;
while(!q.empty()){
pair<int,int> cur_p=q.front();
q.pop();
for(int i=0;i<4;++i){
int cur_x=cur_p.first+step[i][0];
int cur_y=cur_p.second+step[i][1];
if(cur_x>=0&&cur_x<sign.size()&&cur_y>=0&&cur_y<sign[0].size()&&!sign[cur_x][cur_y]&&abs(heights[cur_p.first][cur_p.second]-heights[cur_x][cur_y])<=mid){
q.push({
cur_x,cur_y});//存储广度路径
sign[cur_x][cur_y]=true;//标识
}
}
}
//更新范围
if(sign.back().back()){
right=mid;
}
else{
left=mid+1;
}
}
//返回
return left;
}
};