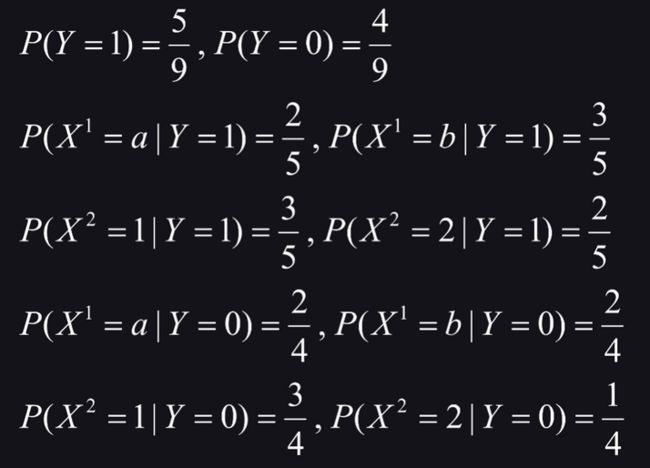第九课.朴素贝叶斯分类器

朴素贝叶斯算法原理

若$P(X)$表示事件$X$发生的概率；$P(Y|X)$表示事件$X$发生的条件下，事件$Y$发生的概率（简称条件概率）；$P(X,Y)$表示事件$X$和事件$Y$同时发生的概率（简称联合概率），则三者有如下的关系：
$$P(X,Y)=P(X)P(Y|X)=P(Y)P(X|Y)$$
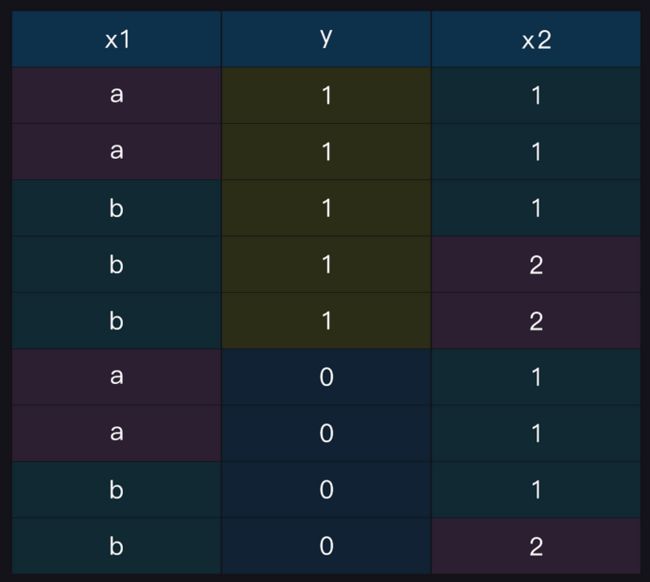
通过联合概率$P(X,Y)$可以得到随机变量$X$和$Y$的边缘概率：$P(X)$和$P(Y)$，如下所示：

图中随机变量$X$的取值为{1,2}，随机变量$Y$的取值为{0,1}，中心区域是$X$和$Y$的联合概率，边缘部分是$X$和$Y$的边缘概率，都满足概率之和为1；图中，中心区域第一行和第二行对应位置相加得到的是$X$的边缘概率；中心区域第一列和第二列对应位置相加得到的是$Y$的边缘概率；

假设先发生了随机事件$Y$，后发生了随机事件$X$，两者存在因果关系：原因$Y$ ==>结果$X$，则随机事件$X$发生的概率$P(X)$可以表示成如下形式：
$$P(X)=\sum _{Y}P(Y)P(X|Y)$$
这个公式叫做全概率公式，它表达的意义是：随机事件$X$的发生可能与多个原因有关，考虑全部原因引起事件$X$发生的概率总和即为随机事件$X$发生的概率；

另一方面，全概率公式也可以通过下面的变换过程得到：
$$P(X)=\sum _{Y}P(X,Y)=\sum _{Y}P(Y)P(X|Y)$$
由联合概率的表达式可以得到贝叶斯公式：
$$P(Y|X)=\frac{P(X,Y)}{P(X)}$$
将公式中的分母写成联合概率的形式，得到贝叶斯公式的第二种写法：
$$P(Y|X)=\frac{P(X,Y)}{{\sum }_Y^{}P(X,Y)}$$
将联合概率展开，得到贝叶斯公式的第三种写法：
$$P(Y|X)=\frac{P(Y)P(X|Y)}{{\sum }_Y^{}P(Y)P(X|Y)}$$
若随机变量$X$的取值为样本特征向量，随机变量$Y$的取值为样本类别标记，则$P(Y|X)$就变成了一个分类模型：贝叶斯分类器。类比逻辑回归的分类算法，只需将概率分布$P(Y|X)$中概率最大值对应的类别作为预测分类就可以。相应地，贝叶斯公式可以写成如下形式：
$$P(Y=c_k|X=x)=\frac{P(Y=c_k)P(X=x|Y=c_k)}{{\sum }_{k=1}^{K}P(Y=c_k)P(X=x|Y=c_k)}$$
特征向量$x=[x^1,x^2,...,x^j,...,x^n]\in R^n$，每个特征$x^j$可以有$S_j$个取值，其中$k\in \left\{1,2,...,K\right\}$表示类别标记$c_k$的取值有$K$个；

公式中的分母部分是全概率表达式，分子中的$P(Y)$称为类别$Y$的先验概率，$P(X|Y)$称为类别$Y$确定后的条件概率，贝叶斯公式计算的$P(Y|X)$称为后验概率；

若事件$X$和事件$Y$相互独立，则随机变量$X$和$Y$的联合概率变为：
$$P(X,Y)=P(X)P(Y)$$
由于$P(X|Y)$中$X$的取值为样本特征向量，故$P(X|Y)$实际上是类别确定条件下的多维随机变量的联合概率分布。假设样本的各个特征在类别确定的条件下是相互独立的，则贝叶斯公式变为朴素贝叶斯公式：
$$P(Y=c_k|X=x)=\frac{P(Y=c_k){\prod }_{j=1}^{n}P(X^j=x^j|Y=c_k)}{{\sum }_{k=1}^{K}P(Y=c_k){\prod }_{j=1}^{n}P(X^j=x^j|Y=c_k)}$$
前面做过一个假设：原因$Y$ ==>结果$X$，在这里依然成立，即：假设样本类别决定了样本的属性特征。举个例子：猫有四条腿，狗有四条腿，人有两条腿。由此可知，朴素贝叶斯是在已知结果$X$的条件下，探求原因$Y$发生的概率，如图所示：

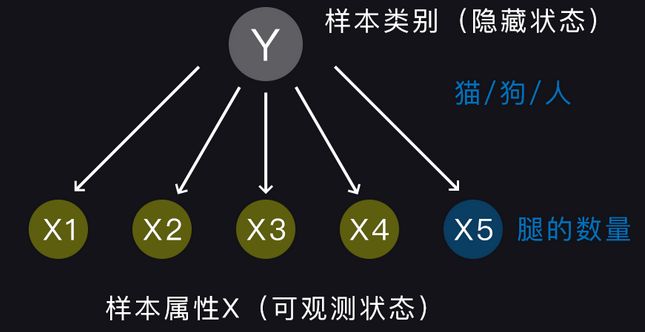
朴素贝叶斯是概率图模型的一种，图中各个特征之间没有边相连表示特征是条件独立的。同时，特征是可以观测到的，如特征$X^5$表示腿的数量；而样本类别是未知的，是机器需要去识别和探求的隐藏状态，如：猫，狗，人；

特征的条件独立性假设是朴素二字的由来，给定样本特征向量之后，朴素贝叶斯分类器取后验概率最大值对应的样本类别作为预测分类，如下所示：
$$y=argma{x}_{c_k}P(Y=c_k|X=x)=argma{x}_{c_k}\frac{P(Y=c_k){\prod }_{j=1}^{n}P(X^j=x^j|Y=c_k)}{{\sum }_{k=1}^{K}P(Y=c_k){\prod }_{j=1}^{n}P(X^j=x^j|Y=c_k)}$$
其中，arg是参数arguments的缩写。因为分母对于所有的样本类别是相同的，不影响函数最大值点的确定，所以朴素贝叶斯分类器的表达式可以简化为：
$$y=argma{x}_{c_k}P(Y=c_k)\prod _{j=1}^{n}P(X^j=x^j|Y=c_k)$$
朴素贝叶斯分类器将后验概率最大的样本类别作为预测分类，在计算上等价于将联合概率最大的样本类别作为预测结果；

朴素贝叶斯参数估计

由上面的朴素贝叶斯分类器表达式可知，模型的参数估计实际上是从训练数据中学习概率分布：

• $P(Y=c_k)$属于一个先验概率分布；
• ${\prod }_{j=1}^{n}P(X^j=x^j|Y=c_k)$为$n$个条件概率分布；
• $k\in \left\{1,2,...,K\right\}$；

第一行公式是样本类别取值的先验概率分布，比如：$P(Y=0)=0.3$，$P(Y=1)=0.7$；第二行公式是样本类别确定的条件下样本各个特征取值的概率分布，比如类别取值为0时，特征$X^1$取值的概率分布：$P(X^1=2|Y=0)=0.4$，$P(X^1=6|Y=0)=0.6$；

上述公式中，样本类别有$K$个取值，样本特征有$n$个，每个特征比如特征$X^j$可以有$S_j$个取值，故需要估计的参数量为：
$$K+K\sum _{j=1}^n{S}_j$$
也就是说，需要利用训练数据计算出如上数量的概率值作为朴素贝叶斯分类器的模型参数，下面介绍两种参数估计方法：极大似然估计和贝叶斯估计；

极大似然估计

先验概率的极大似然估计为：
$$P(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)}{N},k\in \left\{1,2,...,K\right\}$$
其中，$y_i$是样本类别标记，$N$是样本数量，分子是指示函数（条件成立时为1，否则为0）的累加，统计各类样本在训练数据中的占比即为等式左边待求的概率值，如图所示：

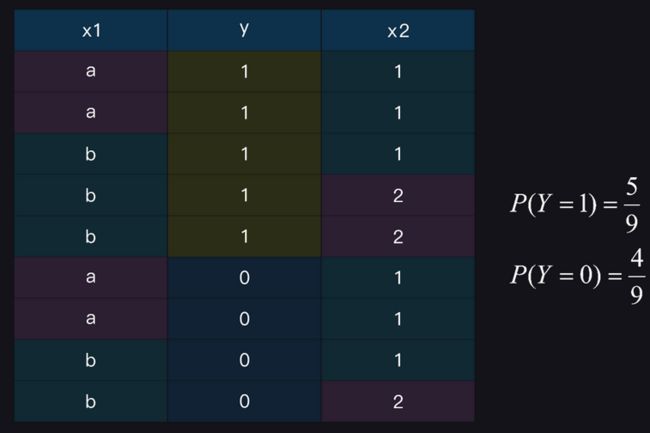
图中的每一行作为一条样本数据，$X^1$和$X^2$是样本特征，$Y$是样本类别标记；

在样本类别确定的条件下，每个特征取值概率的极大似然估计为各类样本中该特征取值的占比，计算公式如下：
$$P(X^j=x^j|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(X_i^j=x^j,y_i=c_k)}{{\sum }_{i=1}^{N}I(y_i=c_k)}$$

贝叶斯估计

极大似然估计的一个缺点是：当训练数据较少时，无论是先验概率还是条件概率的计算，分子部分的统计量都有可能为零，只要有一个为零，代入朴素贝叶斯计算公式中结果就为零，这将给分类结果带来很大的偏差。

采用贝叶斯估计可以解决上面的问题，先验概率和条件概率的贝叶斯估计如下：
$$P_{\lambda }(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)+\lambda }{N+K\lambda }$$
$$P_{\lambda }(X^j=x^j|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(X_i^j=x^j,y_i=c_k)+\lambda }{{\sum }_{i=1}^{N}I(y_i=c_k)+S_j\lambda }$$
其中，$\lambda >0$；相比于极大似然估计，贝叶斯估计在分子和分母上各加了一个大于零的$\lambda$项，当$\lambda =0$时就是极大似然估计，经常取$\lambda =1$，这时称为拉普拉斯平滑；

使用贝叶斯估计得到的先验概率分布和条件概率分布满足：
$$P_{\lambda }(Y=c_k)>0$$
$$P_{\lambda }(X^j=x^j|Y=c_k)>0$$

朴素贝叶斯算法流程

给定样本特征向量$x=[x^1,x^2,...,x^n]$，使用朴素贝叶斯算法分类的流程如下：

• 计算先验概率和条件概率，可以使用上文提到的极大似然估计，也可以使用贝叶斯估计；
• 计算条件独立的联合概率：
  $$P(Y=c_k)\prod _{j=1}^{n}P(X^j=x^j|Y=c_k),k\in \left\{1,2,...,K\right\}$$
  对于给定的样本特征向量，各个特征的取值是确定的。而在算法的第一步中，已经计算了所有特征所有取值的概率值，所以在这一步中，只需要查找相关参数代入计算即可；
• 输出联合概率最大的类别：
  $$y=argma{x}_{c_k}P(Y=c_k)\prod _{j=1}^{n}P(X^j=x^j|Y=c_k)$$
  联合概率最大等价于后验概率最大，朴素贝叶斯将后验概率最大的类别作为输出；

比如有如下数据集：

使用极大似然估计得到：

使用上述朴素贝叶斯分类器进行分类，则样本$X=[a,2]$的类别标记计算过程如下：

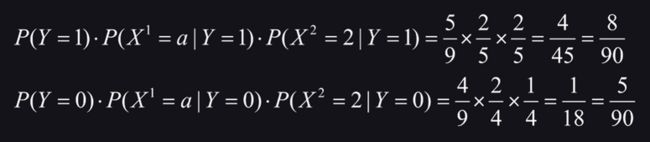
由上述联合概率的计算结果可知，$Y=1$的后验概率大于$Y=0$的后验概率，故样本$X=[a,2]$的类别标记是1

实验：Numpy实现朴素贝叶斯分类器

实验会使用 python 的一些基本代码来实现朴素贝叶斯分类算法，然后利用该算法在鸢尾花(iris)数据集上完成分类任务；

加载莺尾花数据集，并抽取出标签为0和1两类的对应数据：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载鸢尾花(iris)数据集的特征和标记值
X, y = load_iris(return_X_y=True)
print(X.shape,y.shape)
# (150, 4) (150,)
print(set(y))
# {0, 1, 2}

# 使用布尔值索引序列取前两类（0和1）数据的特征和标记
X, y = X[y!=2], y[y!=2] 
print(X.shape,y.shape)
# (100, 4) (100,)
print(set(y))
# {0, 1}

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=2021)

根据算法原理可实现模型：

import pickle
import numpy as np
from collections import  Counter

class NaiveBayes(object):
    '''朴素贝叶斯算法实现'''
    def __init__(self,_lambda=1):
        '''
        _lambda = 0 为极大似然估计；_lambda = 1 为拉普拉斯平滑（贝叶斯估计）
        '''
        self._lambda = _lambda
        # 样本类别的先验概率
        self.prior_probability = dict()
        # 各个特征的条件概率
        self.conditional_probability = dict()
    
    # 模型训练
    def fit(self,X_train,y_train):
        '''
        X_train: m x n 的 numpy 二维数组
        y_train：有 m 个元素的 numpy 一维数组
        '''
        # 1. 估计先验概率
        # 样本类别的数量 K
        K = len(set(y_train)) 
        # 遍历样本类别的取值 y 和每个取值的样本数量 count
        for y,count in Counter(y_train).items():
            # 根据上节课的公式计算样本类别取值为 y 的先验概率 tmp
            tmp = (count + self._lambda) / (len(y_train) + K * self._lambda)
            self.prior_probability[y] = tmp
    
        # 2. 估计条件概率
        # 遍历样本类别的取值 y ；每个取值的样本数量用不到，故用变量 _ 表示
        for y,_ in Counter(y_train).items():
            # 使用字典存储类别确定的条件下，样本各个特征取值的概率分布
            self.conditional_probability[y] = dict()
            # 遍历每列特征 x 和对应的索引值 i（由于是行优先遍历，故对 X_train 转置）
            for i,x in enumerate(X_train.T):
                # 使用字典存储当前类别条件下，第 i 个特征 x (m,) 的概率分布
                self.conditional_probability[y][i] = dict()
                # 通过布尔值索引序列取特征 x 中样本类别为 y 的数据 _x
                _x = x[y_train==y]
                # 特征 x 的取值数量
                S_j = len(set(x))
                
                # 初始化特征 x 取值的概率分布：每个取值的概率均为 tmp ，和小于1
                for x_value in set(x):
                    tmp = (0 + self._lambda) / (len(_x) + S_j * self._lambda)
                    self.conditional_probability[y][i][x_value] = tmp
                
                # 在类别为 y 的样本中，统计特征 x 的取值和每个取值的样本数量
                for x_value,x_count in Counter(_x).items():
                    # 更新当前特征 x 取值为 x_value 的概率
                    tmp = (x_count + self._lambda) / (len(_x) + S_j * self._lambda)
                    self.conditional_probability[y][i][x_value] = tmp
                    
        # 3. 保存模型参数          
        self.save_model()
        
        return self
    
    # 模型预测
    def predict(self,X_test):
        '''
        X_test: m x n 的 numpy 二维数组，m 是样本数，n 是特征数
        '''
        # 类别预测结果
        result = []
        # 遍历每行测试样本
        for sample in X_test:
            # 初始化最大的联合概率和对应的预测分类
            max_prob,y_pred = -1,None
            # 遍历所有类别取值
            for y in self.prior_probability.keys():
                # 计算类别 y 对应的联合概率 = 先验概率与各个特征条件概率的连乘
                joint_probability = self.prior_probability[y]
                # 遍历测试样本各个特征的索引和取值
                for i,x in enumerate(sample):
                    # 对于未知特征取值的条件概率，直接查概率分布字典会出现 KeyError
                    try:
                        joint_probability *= self.conditional_probability[y][i][x]
                    # 由于已有概率分布各概率值的和为1，故设置一个很小的不为零的数
                    except KeyError:
                        joint_probability *= 1e-20
                # 更新最大的联合概率和对应的样本分类
                if joint_probability > max_prob:
                    max_prob,y_pred = joint_probability,y
            # 添加当前测试样本的预测结果
            result.append(y_pred)

        return np.array(result)
    
    # 保存模型参数
    def save_model(self):
        pickle.dump([self.prior_probability,
                     self.conditional_probability],open('nb.model','wb'))

    # 加载模型参数
    def load_model(self):
        p1,p2 = pickle.load(open('nb.model','rb'))
        self.prior_probability = p1
        self.conditional_probability = p2

模型实例化，训练，预测：

# 实例化一个对象
model = NaiveBayes()
# 在训练集上训练
model.fit(X_train,y_train)
# 在测试集上预测
y_pred = model.predict(X_test)

模型加载参数，预测：

# 实例化一个对象
model = NaiveBayes()
# 加载训练好的模型参数
model.load_model()
# 在测试集上预测
y_pred = model.predict(X_test)

对比numpy实现的朴素贝叶斯分类算法和 sklearn 中封装的算法：

# GaussianNB 假设特征的条件概率为正态分布
from sklearn.naive_bayes import GaussianNB

# 实例化一个对象
model_1 = NaiveBayes()
model_2 = GaussianNB()
# 在训练集上训练
model_1.fit(X_train,y_train)
model_2.fit(X_train,y_train)
# 在测试集上预测
y_pred_1 = model_1.predict(X_test)
y_pred_2 = model_2.predict(X_test)
# 也可以一步到位：训练和预测
y_pred_1 = model_1.fit(X_train,y_train).predict(X_test)
y_pred_2 = model_2.fit(X_train,y_train).predict(X_test)

对比两个模型分别在准确率、精确率、召回率、F1值上的表现：

import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score

metrics = dict()

acc_1 = accuracy_score(y_test,y_pred_1)
acc_2 = accuracy_score(y_test,y_pred_2)
metrics['准确率'] = [acc_1,acc_2]

pre_1 = precision_score(y_test,y_pred_1)
pre_2 = precision_score(y_test,y_pred_2)
metrics['精确率'] = [pre_1,pre_2]

rec_1 = recall_score(y_test,y_pred_1)
rec_2 = recall_score(y_test,y_pred_2)
metrics['召回率'] = [rec_1,rec_2]

f1_1 = f1_score(y_test,y_pred_1)
f1_2 = f1_score(y_test,y_pred_2)
metrics['F1值'] = [f1_1,f1_2]

# 通过 dataframe 表格化的形式输出模型的评估指标
pd.DataFrame(metrics,index=['model_1','model_2'])

得到结果：