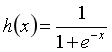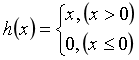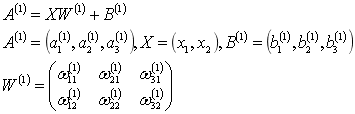深度学习笔记(一)深度学习入门——基于Python的理论与实现
笔记来自斋藤康毅的《深度学习入门–基于Python的理论与实现》
这本书用简洁的语言讲解了比较基础的原理,适合初学者了解。
Numpy和Matplotlib
1.Numpy
NumPy数组提供了便捷的计算数组和矩阵的方法,比较常用。
(1)生成NumPy数组与访问
import numpy as np
x = np.array([1.0, 2.0, 3.0]) # 一维数组
y = np.array([2.0, 4.0, 6.0]) # 一维数组
A = np.array([[1, 2], [3, 4]]) # N维数组
B = np.array([[3, 0], [0, 6]]) # N维数组
print(x[0])
print(A[0][1])
(2)算术运算
# 运算规则
print(x + y) # [3. 6. 9.]
print(x - y) # [-1. -2. -3.]
print(x * y) # [ 2. 8. 18.]
print(x / y) # [0.5 0.5 0.5]
print(A + B) # [[ 4 2][ 3 10]]
print(A * B) # [[ 3 0][ 0 24]]
(3)广播
不同数组运算可以改变维数,原理与矩阵相乘一致.
(m,s)*(s,n)----->(m,n)
(4)其他使用技巧
x = numpy.zeros(6) #创建一维长度为6的,元素都是0一维数组
x = numpy.ones((2,3)) #创建一维长度为2,二维长度为3的二维1数组
x = numpy.empty((3,3)) #创建一维长度为2,二维长度为3,未初始化的二维数组
print numpy.arange(6) # [0,1,2,3,4,5,] 开区间
print numpy.arange(0,6,2) # [0, 2,4]
x = numpy.array([1,2.6,3],dtype = numpy.int64) # 设置数据类型
y = x.astype(numpy.int32) # 使用astype复制数组,并转换类型
# 布尔索引
y = numpy.array([True,False,True,False,True,False])
print x[y==False] # [2,1,0]
# 转置(矩阵)数组:T属性 : mT[x][y] = m[y][x]
2.Matplotlib
Matplotlib是 Python 的绘图库。 它可与 NumPy 一起使用,提供了一种有效的 MatLab 开源替代方案。使用方法几乎与matlab一致。
(1)基本绘图
plt.plot(x,y) # 绘图
plt.show() # 展示图形
plt.title("Matplotlib demo") # 标题
plt.xlabel("x axis caption") # x轴/y轴标题
(2)改变图像标记
plt.plot(x, y, '+', 'b')
(3)subplot()
plt.subplot(2, 1, 1)
建立(2,1)的窗口,在第1个位置绘图
二、感知机
1.运行原理
多个输入——>一个输出(0或1)
当信号*权重之和大于某个阈值θ时,输出1
表达式为:
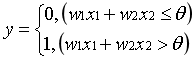
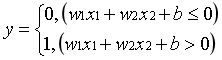
b为偏置参数.
使用感知机可以表示与门、与非门、或门等逻辑电路.
与门、与非门、或门只有参数的值即权重和阈值不同。
2.局限性和优势
无法实现异或门。
局限性在于感知机只能表示由一条直线分割的线性空间,而异或门只能用曲线分割为非线性空间,
优势在于可以“叠加层”,通过叠加层来表示异或门。
3.多层感知机
利用与门、或门和与非门可以形成异或门
(1)第0层的两个神经元接受输入信号,并将信号发送至第一层的神经元;
(2)第1层的神经元将信号发送至第2层的神经元,第2层的神经元输出y.
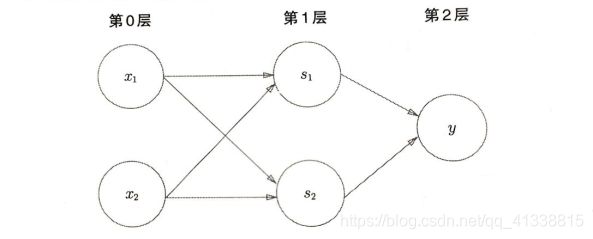
感知机通过叠加层能够进行非线性的表示,理论上可以表示计算机进行的处理。
三、神经网络
神经网络的一个重要的性质就是它可以自动地从数据中学习到合适的权重参数。
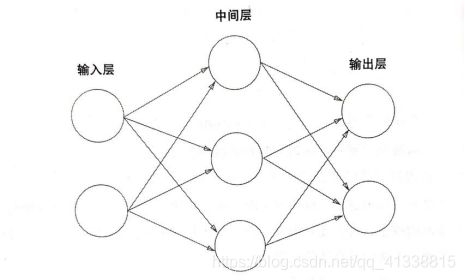
1.神经网络的基本结构
2.激活函数
引入h(x),其作用在于决定如何来激活输入信号的总和:
y=h(b+w1x1+w2x2)
a=b+w1x1+w2x2
y=h(a)
节点a即为信号的加权总合,或者称为神经元.
(1)sigmoid函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
绘图
def main():
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1, 1.1)
plt.show()
(2)阶跃函数
Python实现比较简单,if条件分支语句即可。
(3)非线性函数
阶跃函数和sigmoid函数都是非线性函数,为了发挥叠加层带来的优势,激活函数必须使用非线性函数。
(4)ReLU函数
def relu(x):
return np.maximum(0, x)
3.多维数组的运算
与matlab中矩阵相乘类似
神经网络的内积等于X矩阵和W矩阵的点积
Y = np.dot(X, W)
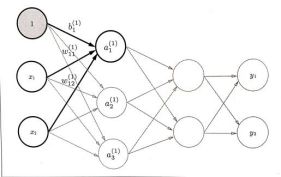
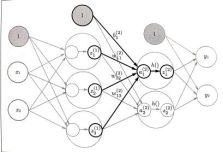
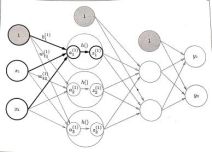
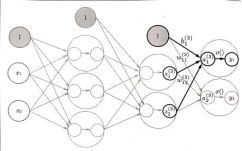
4.三层神经网络的实现
输入层有2个神经元,第1个隐藏层有3个神经元,第2个隐藏层有2个神经元,输出层有2个神经元。
W12(1):
12下标代表前一层的第2个神经元到后一层的第1个神经元的权重;
(1)上标代表权重和神经元的层号为1。
import numpy as np
from sigmoid_function import sigmoid
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)
print(A1) # [0.3 0.7 1.1]
print(Z1) # [0.57444252 0.66818777 0.75026011]
定义了identity_function()函数,将其作为输出层的激活函数,恒等函数会将输入按原样输出。
总共三层神经元
import numpy as np
from sigmoid_function import sigmoid
def init_network():
network = {
}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.3, 0.5])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def identity_function(x):
return x
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
if __name__ == '__main__':
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)
5.输出层设计
softmax函数——恒等函数即σ,输入信号原封不动地被输出。做分类问题时(判断数据属于哪一类),会用到softmax函数:
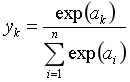
n即为输出层的神经元,用人话说:最终输出等于输出层求指数后在输出总和中的占比。相当于用概率的方法处理问题。
但softmax不适合做太大数字的运算,会产生溢出现象,可以将表达式进行改进,分子分母同乘相同的常数,一般使得logC等于输入信号中的最大值。
import numpy as np
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
6.手写数字识别
(1)MINIST数据集
非常常用的手写数字图像集,由0-9的数字图像构成,一般使用方法为,先用训练图像进行学习,再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。
load_mnist()函数以(训练图像,训练标签),(测试图像,测试标签)的形式返回读入的MNIST数据。
选择参数FLATTEN等于True的话,读入的MNIST图像数据会转化为一维数组,需要用reshape函数进行调整后才能绘图,同时也需要使用PIL库展示图像。
(2)神经网络的推理
输入层有784个神经元即28*28=784个像素,输出层有10个神经元,数字来源于10类别分类(即数字0-9),两个隐藏层,第一个隐藏层有50个神经元,第二个隐藏层有100个神经元。
主函数如下:
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 获取概率最高的元素的索引
if p == t[i]:
accuracy_cnt += 1
获取数据——初始化神经网络(读入参数)——循环推导神经网络——将回答正确的概率作为识别精度。
np.argmax(array, axis)函数用于返回一个numpy数组中最大值的索引值。当一组中同时出现几个最大值时,返回第一个最大值的索引值。
运行函数得到Accuracy:0.9352,表示有93.52%的数据正确分类了。
另外,可以使用normalize将图像像素值除以255进行正规化,使得数据都在0.0-1.0的范围内,这种预处理方式可以提高识别性能和学习效率。
(3)批处理
前面的神经网络的推导是基于单张图像形成的,如果我们考虑打包输入多张图像的情形,比如100张,则需要使得输入图像X形状变为100784,输出Y也相应地变成了10010.
这样打包输入的数据称为批,可以大幅度缩短每张图像的处理时间。
基于批的代码实现:
x, t = get_data()
network = init_network()
batch_size = 100
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i + batch_size]
y_batch = predict(network, x_batch)
p= np.argmax(y_batch, axis=1) # 获取概率最高的元素的索引
accuracy_cnt += np.sum(p == t[i:i + batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
range(start,end,step)可以用来生成列表,
axis=1代表沿着一维方向寻找值最大的元素索引。axis对应的是剥掉的中括号的位置,具体见下面博客。
https://blog.csdn.net/weixin_42755982/article/details/104542538
运行结果仍然是Accuracy:0.9352
四、神经网络的学习
1.从数据中学习
对于线性可分问题,根据“感知机收敛定理”,通过有限次数的学习,线性可分问题是可解的。但是非线性可分问题无法通过学习解决。
解决问题有以下三种方法:
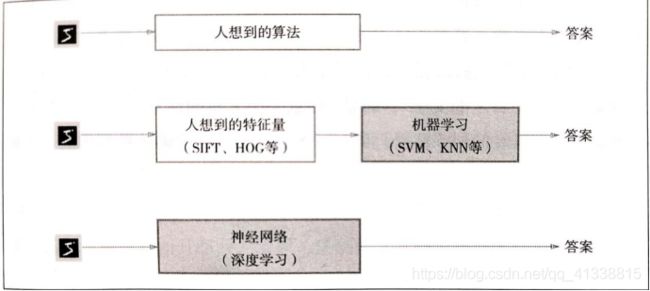
通过算法解决,通过对特征量的机器学习解决,通过神经网络对图像进行深度学习。特征量仍然是人所想到的,设计的,而在神经网络中,图像中包含的重要特征量也都是由机器来学习。深度学习也被称为端对端学习,从原始数据中获得目标结果,其优点就是对所有问题都可以用同样的流程来解决。
获得泛化能力是机器学习的最终目标。泛化能力指的是处理未被观察过的数据的能力。一般将数据分为训练数据和测试数据两部分来进行学习和实验。首先,使用训练数据进行学习,寻找最优的参数,然后,使用测试参数评价训练得到的模型的实际能力。
2.损失函数
神经网络的学习中所用的指标称为损失函数,表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合。这个损失函数可以使用任意函数,但是一般用均方误差和交叉熵误差等。
(1)均方误差
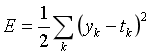
yk代表神经网路的输出,tk表示监督数据,k表示数据的维数。
代码与测试:
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y - t) ** 2)
if __name__ == '__main__':
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(mean_squared_error(np.array(y), np.array(t)))
结果:0.09750000000000003
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]这种表示方式被称为one-hot表示。
(2)交叉熵误差
![]()
当监督数据为one-hot形式时,交叉熵误差的值时由正确解标签所对应的输出结果决定的。
代码与测试:
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
if __name__ == '__main__':
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
print(cross_entropy_error(np.array(y), np.array(t)))
结果:0.510825457099338
加上微小值delta=1e-7可以防止负无穷大的产生。
(3)mini-batch学习
求所有训练数据的损失函数的总和如下:
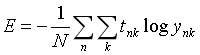
假设数据有n个,tnk代表第n个监督数据的第k个元素。
神经网络的学习一般需要从全部数据中选取一批数据(称为mini-batch),对每个mini-batch进行学习。在mini-batch下,交叉熵误差的格式也需要发生少许改变:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
对于mini-batch的学习在后面的部分进行。
3.数值微分
在进行神经网络的学习时,不能将识别精度作为指标,因为参数的导数在绝大多数地方都会变为0。而参数的导数是寻找最优参数的途径,不断更新计算参数的导数,找到损失函数下降的最大方向,从而逐步更新参数的值。
(1)导数
一般数值微分采用数值方法近似求解函数的导数,比如中心差分、向前差分等等,代码实现非常简单:
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
(2)偏微分
其实偏微分本质上和导数是一样的,只需要将其他量全部固定为某个值。
4.梯度
计算各个参数在某点处的偏导数,得到一个形状和参数相同的梯度数组。
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
np.zeros_like(x)会生成一个形状和x相同、所有元素都为0的数组。
梯度表示的是各点处的函数值减小最多的方向,函数的极小值、最小值以及被称为鞍点的地方,梯度为0.寻找最小值的梯度法称为梯度下降法,对应的有梯度上升法。
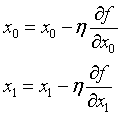
η表示更新量,或者称为学习率,代表了更新参数的程度。
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
学习率太大或者太小都可能会得到不好的结果,学习率太大时会发散成一个很大的值,学习率过小,需要的步数会很多。
神经网络的梯度是指损失函数关于权重参数的梯度,梯度的表达式与权重矩阵形状相同:
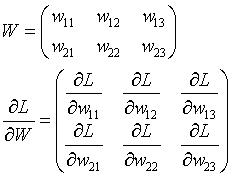
5.学习算法的实现
原理很简单:
选出mini-batch——计算梯度——更新参数——重复步骤
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
#grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
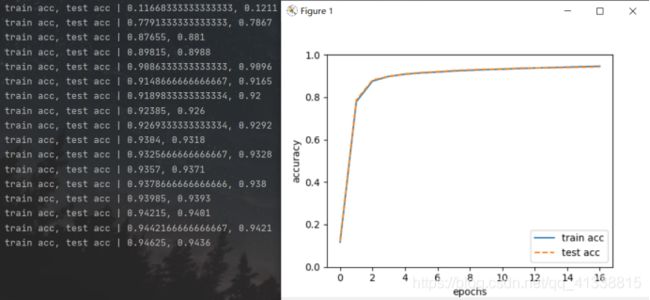
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 绘制图形
markers = {
'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()