快速排序(双指针法、挖坑法、前后指针法)递归、非递归实现
前言
快速排序是交换排序中的一种,是Hoare于1962年提出的一种二叉树结构的交换排序方法,类似于二叉树的前序遍历。
主要思想:
■ 任取待排序元素序列中的某元素作为关键字。
■ 按照该关键字将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值。
■ 然后将左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
区间划分左右部分常见方式
1、双指针法
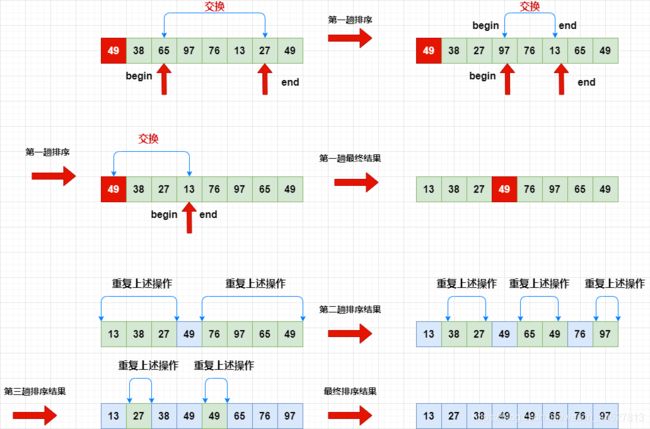
实现过程:如下图 !
过程总结:
■先将begin的索引作为keyIndex记录下来,然后使用两个指针,一个指向end,一个指向begin。
■让end指针先走,找比arr[keyIndex]小的值。然后begin指针开始走,找比arr[keyIndex]大的值。
■然后将begin指针和end指针找到的值交换,重复上述过程直到begin和end指针相遇。
■最后将a[end]和a[keyIndex]交换。
C语言代码实现
int PartSort1(int* a, int begin, int end) {
int keyIndex = begin;
//注意一定要让end先移动
while (begin < end) {
while (begin < end && a[end] >= a[keyIndex]) end--;//注意这个地方一定要取等
while (begin < end && a[begin] <= a[keyIndex]) begin++;//注意这个地方一定要取等
swap(a + begin, a + end);
}
swap(a + end, a + keyIndex);
return begin;
}
注意代码中的细节
代码中注释地方一定要取等
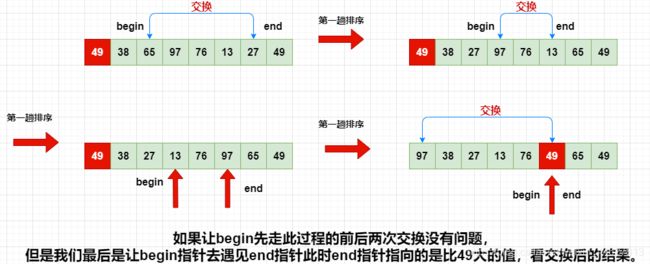
看这种情况,如下图!!
选最左边的值为关键字,一定要让end先走,相反选最右边的值,让begin先走
究其原理:哪个指针先走,关键字最后就与那个指针找的值交换,我们的end指针是找的比key小的值,而begin找的是比key大的值。我们的关键字是第一个,所以最后要将比关键字小的值换到关键字现在的位置上。所以要让end先走。如果我们选取最后一个作为关键字,那么就要让begin先走。
2、挖坑法
实现过程:如下图 !
过程总结:
■先将a[begin]的key值保留下来形成坑,然后使用两个指针,一个指向end,一个指向begin。
■让end指针先走,找比key小的值,让a[begin]=a[end],此时end位置形成新坑。然后begin指针开始走,找比key大的值。然后让a[end]=a[begin],此时end指针形成新坑。
■重复上述过程,最后让begin和end指针相遇。
■最后a[begin]=key,将key的值填入坑当中。
C语言代码实现
int PartSort2(int* a, int begin, int end) {
int key= a[begin];
while (begin < end) {
//一定要然end先走
while (begin < end && a[end] >= key) end--;//一定要让a[end]>=key,一定要取等。
a[begin] = a[end];
while (begin < end && a[begin] <= key) begin++;//一定要让a[begin]<=key,一定要取等。
a[end] = a[begin];
}
a[begin] = key;
return begin;
}
注意代码中的细节
代码中注释地方一定要取等
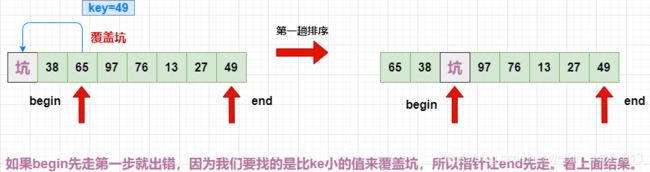
看这种情况,如下图!!
选最左边的值为关键字,一定要让end先走,相反选最右边的值,让begin先走
究其原理:我们选取第一个元素作为坑,所以要选择比key小的值来覆盖坑,所以要让end先走。如果我们选最后一个作为坑,那么我们就要让begin先走。
3、前后指针法
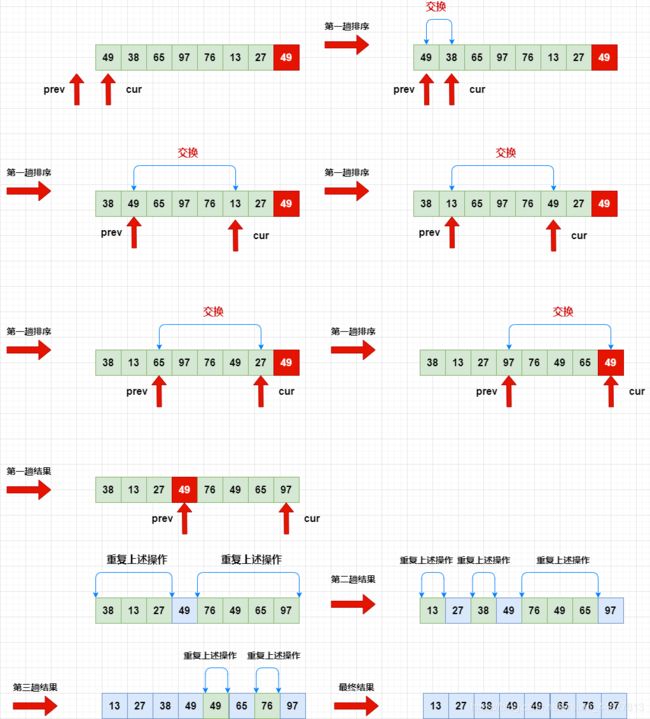
实现过程:如下图 !
过程总结:
■先将a[end]的最为关键字,然后使用两个指针,一个指针prev指向begin-1,一个指针cur指向begin。
■当a[cur]
■重复上述过程,直到cur==end。
■最后++prev,然后a[++prev]和a[end]交换。
C语言代码实现
int PartSort3(int* a, int begin, int end) {
int prev = begin- 1, cur = end;
while (cur < end) {
if (a[cur] < a[end] && ++prev!=cur) {
swap(a + prev, a + cur);
}
cur++;
}
swap(&a[++prev],&a[end]);
return prev;
}
递归实现快速排序
C语言代码实现
void QuickSort(int* a, int left, int right) {
assert(a);
if (left >= right) {
return;
}
int partition = PartSort2(a,left,right);//随便调用上面三种单区间排序方法,类似于二叉树的前序遍历。
QuickSort(a,left,partition-1);
QuickSort(a, partition+1, right);
}
三数取中优化排序时间复杂度
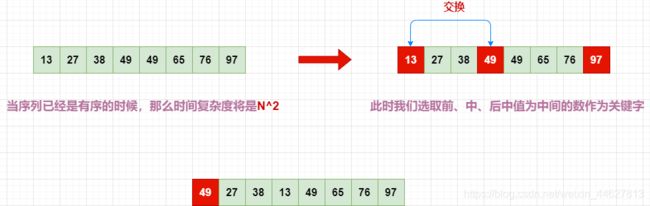
特殊情况看下图 !
我们发现当序列有序时,如果再采取上面的方法,那么时间复杂度将是N^2,所以此时我们选取 前中后 中值为中间的值和关键字的位置进行交换,那么我们再进行排序的序列的时间复杂度基本上被优化为N*logN。
C语言代码实现
int GetMindIndex(int* a, int begin, int end) {
int mid = (begin + end) >> 1;
if (a[mid] < a[begin]) {
if (a[begin] < a[end]) {
return begin;
}
else if (a[end]<a[mid]) {
return mid;
}
else {
return end;
}
}
else {
//a[mid] >= a[begin]
if (a[begin] > a[end]) {
return begin;
}
else if (a[mid] < a[end]) {
return mid;
}
else return end;
}
}
int PartSort2(int* a, int begin, int end) {
int minIndex = GetMindIndex(a, begin,end);
swap(a + begin, a + minIndex);
int key= a[begin];
while (begin < end) {
//一定要然end先走
while (begin < end && a[end] >= key) end--;//一定要让a[end]>=key,一定要取等。
a[begin] = a[end];
while (begin < end && a[begin] <= key) begin++;//一定要让a[begin]<=key,一定要取等。
a[end] = a[begin];
}
a[begin] = key;
return begin;
}
非递归实现快速排序
递归实现快速排序的缺陷
■ 效率稍低:递归建立栈帧有所消耗,但是对于现代计算机,这个被优化得维护其微可以忽略不计,但是数据大了之后还是有所消耗。
■ 容易导致栈溢出:递归最大得缺陷是,当栈帧的深度太深,那么可能导致栈溢出。因为系统栈空间一般不大在M级别。如果我们使用数据结构模拟非递归,数据是存储在堆上的,堆是G级别的空间。
递归该非递归的方法
■ 用循环一些简单递归才能改循环:斐波拉契数列求解等。。
■ 栈模拟存储数据非递归,其实递归的主要思想就是栈,只不过递归是使用的系统栈。
C++代码
void QuickSortNonR(int* a, int left, int right) {
stack<int> stk;
stk.push(right);
stk.push(right);
while (!stk.empty()) {
int begin=stk.top();
stk.pop();
int end = stk.top();
stk.pop();
int partition = PartSort02(a,begin,end);
if (begin<partition-1) {
stk.push(partition - 1);
stk.push(begin);
}
if (partition+1 < end) {
stk.push(end);
stk.push(partition - 1);
}
}
}
快速排序的特性总结
1. 快速排序整体的综合性能和使用场景都是比较好的,如果加了三数取中,那么我们还能较好的避开最坏的情况,所以才敢叫做叫快速排序。
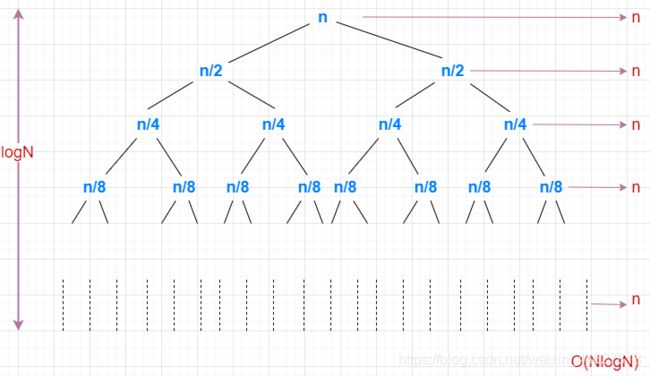
2. 平均时间复杂度:O(NlogN)。最好情况:O(NlogN)。最坏情况:O(N^N)。
3. 空间复杂度:O(logN)~O(N)。
4. 稳定性:不稳定。