EEG源分析思考总结
本文首发在个人博客上(7988888.xyz),此文章中所有链接均通过博客进行访问。
最近,由于高校的放假,我的工作也算是得以空闲起来,有了时间来看看文献学习知识,我在很久之前也写过关于《eeg源分析的简介》,大致也介绍了源分析所需要的东西,这几天我也一直在读以下两篇文献,今天的内容也是对这些东西的思考总结。
文献:
Hallez, H., Vanrumste, B., Grech, R. et al. Review on solving the forward problem in EEG source analysis. J NeuroEngineering Rehabil 4, 46 (2007). https://doi.org/10.1186/1743-0003-4-46
Grech, R., Cassar, T., Muscat, J. et al. Review on solving the inverse problem in EEG source analysis. J NeuroEngineering Rehabil 5, 25 (2008). https://doi.org/10.1186/1743-0003-5-25
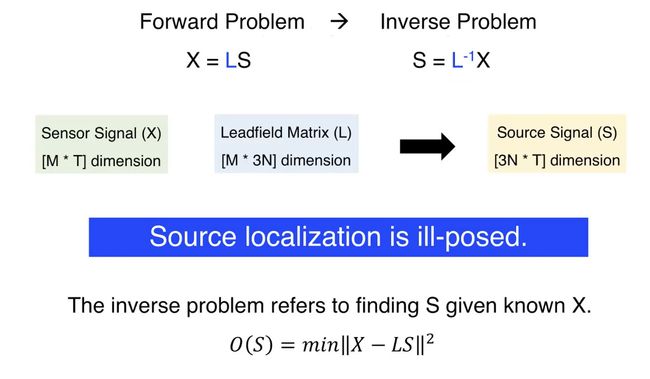
所谓EEG脑源定位,也即EEG逆向问题,也就是根据现有采集得到的头皮脑电信号来反演估计脑内神经活动源的位置、方向和强度大小。从反演的结果来说,脑电逆问题应该是非线性优化问题,考虑到计算的复杂性,所以近似的规约为线性问题X=LS,X表示为头表电极记录到的点位,S是待进行空间定位的源信息向量,L称为传递(增益)矩阵,是脑电正问题头模型等问题的解,可以通过构造合适的头模型等参数来获得。所以提高电极信号的准确性和对合适头模型的确定是比较关键的。
—图片来自B站刘泉影老师neurochat讲座
在上面第一篇文献中谈到脑电信号产生的正向问题,这是一篇综述文章,主要介绍了脑电信号的产⽣机制: 锥体神经元顶树突的突触后电位产生的细胞外电流,然后通过方程模型计算大脑的电导率,比较了在不同的头模型所产生不同数据。
不同头模型计算包括边界元法(BEM)、有限元法(FEM)和有限差分法(FDM)
文献中谈到最开始的头模型—三层同⼼球头模型,在这个模型中,内层代表⼤脑,中间层代表头⻣,外层代表头⽪。

很明显,这样的球头模型并不符合实际情况,因此在后续的发展中就有了基于真实头模型进行计算的三种计算方法。
第一种方法:The boundary element method(BEM)边界元方法
边界元法是⼀种计算分段均匀体积导体中电流源所产⽣的表⾯电位的数值技术。虽然它限制了我们只使⽤各向同性电导率,但由于其计算量⼩,仍然被⼴泛应⽤。这种⽅法在六⼗年代后期起源于⼼电扫描仪,在⼋⼗年代后期进⼊脑电源定位领域。这种⽅法能够通过计算⼀个给定的电流源(如偶极⼦)在体积的表面和边界处的势能值来解决体积问题。surfaces表面分隔体积内不同导电性的区域,⽽边界是与导电体积分隔的⾮导电空⽓外表⾯。实际上,头部模型是从表⾯建⽴的,每个表⾯都有⼀个特定的组织。通常,头部模型由三个surfaces表⾯组成: 头颅界⾯、头颅-头⽪界⾯和外表⾯(如上图9)。假定界⾯之间的区域为均匀各向同性导体。为了得到这样⼀个分段均匀体积的解,每个界⾯⽤⼩的边界元格⼦镶嵌起来。那么正问题的计算就涉及到⽹格上的每个节点,边界元法就计算电极位置对应的节点电位。边界元法的最大优点是,可以使求解问题的空间维数降低一阶,从而使计算工作量及其所需计算机容量大大减小。但是在脑电正演问题中使⽤边界元法的⼀个主要缺点是,当源到其中⼀个表⾯的距离与⽹格中三⻆形的⼤⼩相当时,精度就会下降。
第二种方法:The finite element method(FEM)有限元方法
有限元法中把计算区域划分成一组离散的容积或者叫元体(在二维情形下元件的形状常常是三角形或者四边形),然后通过对控制方程作积分来得出离散方程,有限元法的最大优点是,对于不规则几何区域的适应性好。如上图10,整个三维体积导体被数字化成⼩的元体。
在有限元⽅法中,⼀个重要的思考是如何在模型中表示偶极⼦源?
本文中阐述了五种方法:
1、⽤⼀对相反极性的固定电压条件加在两个相邻节点上来表示偶极⼦
2、另⼀种⽅法是在元体基函数中嵌⼊⼀个偶极源。
3、第三种⽅法是将场分成两部分—⼀部分是理想偶极⼦在⽆限均匀区域中产⽣的标准场,另⼀部分是在封闭⽆源区域中的边界条件下,这种边界条件可以校正电流在不同电导率区域之间的边界移动
4、在拉普拉斯公式中,去除⼀个含有偶极⼦的⼩体积,并在去除体积表⾯的所有节点施加固定边界条件。这可以解释为⽤等效电压源的估计值来代替电流源的值。
5、第五种形式是模糊偶极⼦模型,其中源和汇单极⼦分布在相邻节点上。在⼤多数情况下,源单极⼦和汇单极⼦不重合的节点的有限元⽹格。因此,表示偶极⼦的⼀种⽅法是在相邻节点上放置的单极⼦和。
结果发现,第三种公式对于横向和径向偶极⼦都给出了最佳性能(其次是拉普拉斯公式)。
第三种方法:The finite difference method(FDM)有限差分法
利⽤以单元为中⼼的 iFDM 的盒⼦积分⽅案 ,将带边界条件的微分⽅程转化为线性⽅程。将求解区域用网格线的交点(节点)所组成的点的几何来代替(如上图12),在每个节点上,描述所研究的流动与传导问题的偏微分方程中的每一个导数项用相应的差分表达式来代替,从而在每个节点上形成一个代数方程,其中包含了本节点及其附近一些节点上的所求量的未知值。求解这些代数方程组就获得了所需的数值解。在规则区域的结构化网格上,有限差分法是十分简单而有效的,而且很容易引入对流项的高阶格式。其不足的是离散方程的守恒特性难以保证,而最严重的缺点则是对不规则区域的适应性差。
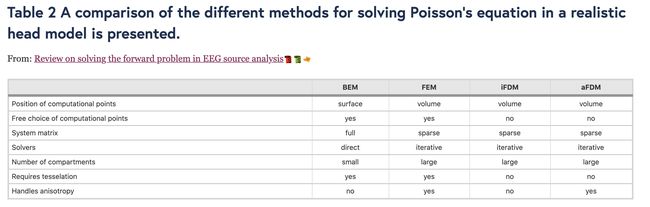
三种计算方法的比较
边界元法与有限元法或有限差分法的第⼀个区别是计算解的区域。边界元法在均匀各向同性分区间的边界上求解,⽽有限元法和有限差分法则在整个体积内求解正问题。
另⼀个重要⽅⾯是计算效率。与边界元法和有限元法相⽐,有限差分法的计算点固定在各向同性⽅法的⽴⽅体中⼼上,⽽各向异性⽅法的计算点固定在⽴⽅体⻆上。在有限元法和边界元法中,计算点、四⾯体顶点和三⻆形顶点可以更⾃由地选择。因此,在节点数⽬相同的情况下,有限元⽅法能够⽐有限差分⽅法更好地表示不同隔室之间的不规则界⾯。然⽽,⽤于获得真实体积导体模型的分割医学图像是⽤⽴⽅体素构造的。从这些分割后的图像直接⽣成⽤于 FDM 的结构化⽹格是很简单的。在有限元法和边界元法中,需要使⽤附加的镶嵌算法分别得到四⾯体单元和⾯三⻆形。
在第二篇文献中就谈到了逆向问题的计算方法:⾮参数⽅法和参数⽅法
第⼀类非参方法,讨论最⼩范数估计及其推⼴,Backus-Gilbert ⽅法,加权分辨率优化,LAURA,收缩和多分辨率⽅法。第⼆类参数方法,讨论⾮线性最⼩⼆乘问题,波束形成⽅法,多信号分类算法,脑电源分析,⼦空间技术,模拟和有限元,以及计算智能算法,特别是神经⽹络和遗传算法
For the first category we discuss minimum norm estimates and their generalizations, the Backus-Gilbert method, Weighted Resolution Optimization, LAURA, shrinking and multiresolution methods. Forthe second category, we discuss the non-linear least-squaresproblem, beamforming approaches, the Multiple-signal Classification Algorithm (MUSIC), the Brain Electric Source Analysis (BESA), subspace techniques, simulated annealing and finite elements, and computational intelligence algorithms, inparticular neural networks and genetic algorithms
逆向求解⽅法主要有两种: ⾮参数⽅法和参数⽅法。⾮参数优化⽅法也被称为分布源模型(Distributed Source Models),分布反解(DIS)或成像⽅法。在这些模型中,⼏个具有固定位置和可能固定⽅位的偶极源分布在整个⼤脑体积或⽪质表⾯。假设它们的来源是⽪层锥体神经元树突⼲的细胞内电流,这些电流通常定向于⽪层表⾯,因此固定定向偶极⼦通常被设定为正常排列,然后估计这些偶极⼦源的振幅和⽅向,由于偶极⼦的位置没有估计,所以问题是线性的。另⼀⽅⾯,在参数化⽅法中,在位置和⽅向未知的模型中假设少数偶极⼦。
除了以上文献外,还推荐查看到得到EEG源定位后还可以做的功能连接文献。
Barzegaran E, Knyazeva MG (2017) Functional connectivity analysis in EEG source space: The choice of method. PLoS ONE 12(7): e0181105. https://doi.org/10.1371/journal.pone.0181105
更多算法的介绍,可参考微信文章《EEG源分析》。
谢谢大家观看,如有帮助,来个喜欢或者关注吧!
本文作者:陈锐
博客地址 : 陈锐博客
知乎地址 : 知乎专栏
B站地址 : B站主页
书店地址 : 书店主页
简书地址 : 简书主页
CSDN地址 : csdn主页